1、枚举法,常用算法之一。例如目前的新冠病例筛查。就针对某个区域或某个单位的特定人群,逐一测验,找到感染者的过程。这种方法虽然暴力,耗费时间、财力和人力,但确是我们目前最优先考虑的,因为枚举法得到的结果总是正确的,不会遗漏最优解。这也是党和国家践行人民至上、生命至上理念的体现。
2、枚举法求解步骤:
(1)枚举范围——定责任、定目标、定措施,聚非常之力,尽担当之责
(2)约束条件——攻坚克难,砥砺奋进


在进行归纳推理时,如果逐个考察了某类事件的所有可能情况,因而得出一般结论,那么这结论是可靠的,这种归纳方法叫做枚举法。枚举法,也称穷举法、暴力法、蛮力法等,就是利用计算机运算速度快、精确度高的特点,对要解决问题的所有可能情况,一个不漏地进行检验,从中找出符合要求的答案,因此枚举法是通过牺牲时间来换取答案的全面性。
枚举法的特点为:
(1)得到的结果肯定是正确的;
(2)可能做了很多的无用功,浪费了宝贵的时间,效率低下。
(3)通常会涉及到求极值(如最大,最小,最重等)。
(4)数据量大的话,可能会造成时间崩溃。
枚举法的设计要关注一下两个方面:
(1)确定枚举的范围
(2)找出约束的条件
在确定枚举对象、枚举范围和约束条件后,就可以枚举可能的解,进而验证是否是问题的解。枚举法可以通过循环+条件判断来实现,对应到伪代码就是for加if。

示例1:百钱买百鸡问题
我国古代数学家张丘建在《算经》一书中提出的数学问题:鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?
解析:
(1)枚举的范围
设公鸡x只,母鸡y只,小鸡z只,则x∈[0,20]、x∈[0,33]、x∈[0,99]
(2)约束的条件
x+y+z=100 and 5x+3y+z/3=100
伪代码如下:
for x=0 to 20
for y=0to 33
forz=0 to 99 step 3
if x+y+z=100 and 5x+3y+z/3=100 then
output x,y,z
endif
endfor
endfor
endfor
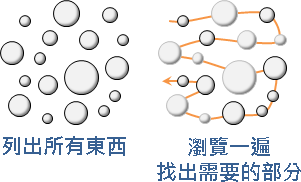
流程图如下:
示例2:猜数字问题
雨水淋湿了算术书的一道题,8个数字只能看清3个,第一个数字虽然看不清,但可看出不是1。求其余数字是什么? [□*(□3+□)]2=8□□9
解析:
(1)枚举范围
从左至右,五个方框,设为A、B、C、D、E。其中:A∈[2,9],B∈[1,9],C∈[1,9],D∈[0,9] ,D∈[0,9]。
(2)约束条件:[A*(B*10+3+C)]^2=8009+D*100+E*10
伪代码如下:
for A=2 to 9
for B=1to 9
forC=1 to 9
forD=0 to 9
for E=0 to 9
if(A*(B*10+3+C))^2=8009+D*100+E*10then
output A,B,C,D,E
endif
endfor
endfor
endfor
endfor
endfor
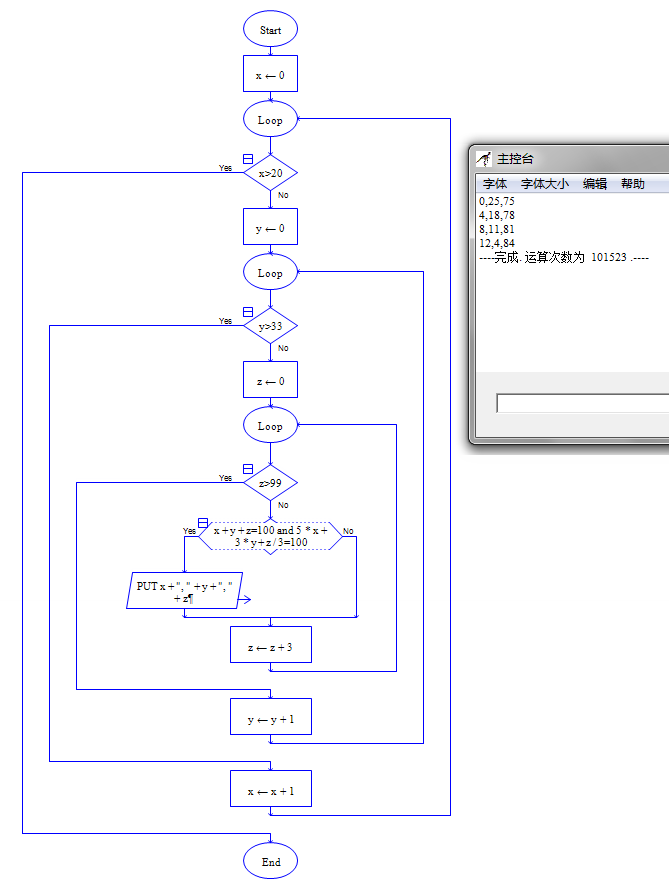
流程图如下: