
1、计算思维的本质(抽象 和 自动)与人工智能与第四次工业革命。
2、计算思维+我+专业,思维如何面向未来准备现在。


2006年3月,美国卡内基 · 梅隆大学计算机科学系主任周以真教授,对计算思维进行了清晰、系统的阐述,使计算思维的概念得到人们的极大关注。
周以真教授说:“计算思维是运用计算机科学的基础概念进行问题求解、系统设计、和理解人类行为等涵盖计算机科学广度的一系列思维活动。”
培养计算思维能力的目的是培养学生像拥有阅读、写作和算术基本技能一样拥有计算思维技能,并能自觉地应用于日常的学习、研究和工作中,要像计算机科学家那样思考问题。


计算思维的本质是抽象和自动。从操作层面上讲,计算就是如何寻找一台计算机去求解问题,隐含地说就是要确定合适的抽象,选择合适的计算机去解释执行该抽象,后者就是自动化。
计算思维中的抽象完全超越物理的时空观,可以完全用符号来表示,其中,数字抽象只是一类特例。与数学相比,计算思维中的抽象显得更为丰富,也更为复杂。数学抽象的特点是抛开现实事物的物理、化学和生物等特性,仅保留其量的关系和空间的形式,而计算思维中的抽象却不仅仅如此。比如算法就是一种抽象,是解决问题的方法和步骤,不能将两个算法简单地放在一起来实现一种并行算法。

抽象层次是计算思维中的一个重要概念,它使人们可以根据不同的抽象层次,进而有选择的忽视某些细节,最终控制系统的复杂性。在分析问题时,计算思维要求将注意力集中在感兴趣的抽象层次或其上下层,还应当了解各抽象层次之间的关系。
计算思维中的抽象最终是要能够机械的一步一步自动执行。为了确保机械的自动化,就需要在抽象过程中进行精确和严格的符号标记和建模,同时也要求计算机系统或软件系统生产厂家能够向公众提供各种不同抽象层次之间的翻译工具。


(1)七桥问题 —— 抽象
18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如右上图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。后来大数学家欧拉把它抽象成一个几何问题(如左图下)——一笔画问题。
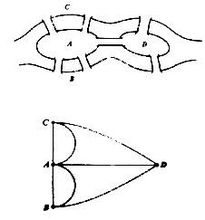
他不仅解决了此问题,证明上述走法是不可能的。且给出了连通图可以一笔画的充要条件是:奇点的数目不是0 个就是2 个(连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两端,因此任何图能一笔画成,奇点要么没有要么在两端)。

(2)取咖啡问题 —— 自动化
在下图中,咖啡杯子和杯盖被放在了左侧,牛奶、糖、咖啡放在中间,而咖啡壶放在了最右侧。谈话者想冲杯咖啡,然后一起交谈,那么他冲咖啡的顺序应该是:
① 首先,取咖啡杯。
② 其次,依次向杯中加入牛奶、糖、咖啡。
③ 再次,咖啡壶冲咖啡。
④ 最后,原路返回,盖好杯盖。

虽然,上述操作符合传统思维逻辑,但从计算思维角度看,上述操作并不是最佳的方案,不符合自动化理念,应该将杯盖的位置调整到咖啡壶旁,冲完咖啡后直接盖上杯盖,而不是原路返回。
(3)求阶乘 —— 思维的多样性
一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。1808年,基斯顿·卡曼引进这个表示法。阶乘的求解可以有两种方法:
① 阶乘的数学定义为:n!=1×2×3×...×n。
② 阶乘的递归定义为:0!=1,n!=(n-1)!×n。
算法是指解决问题的方法和步骤。解决阶乘问题有两种方法,验证了计算思维的多样性。


(1)计算思维是人思维,而非机器思维
计算思维是人类求解问题的一条途径,但决非要使人类像计算机那样地思考。计算机枯燥且沉闷,人类聪颖且富有想象力。是人类赋予计算机激情。配置了计算设备,我们就能用自己的智慧去解决那些在计算时代之前不敢尝试的问题,实现“只有想不到,没有做不到”的境界。
(2)计算思维是能力,而非技能
计算思维能力是每一个人为了在现代社会中发挥职能所必须掌握的。而那些刻板的技能意味着机械的重复。具有讽刺意味的是,当计算机像人类一样思考之后,思维可就真的变成机械的了。

(3)计算思维是概念化的,而非程序化的
学习计算思维课程的目的是要像计算机科学家那样去思维问题,而并非是学习一门编程语言,问题的求解要建立在多个层次上的思维抽象。
(4)计算思维是思想,而非人造品
不只是我们生产的软件、硬件等人造品将以物理形式到处呈现,并时时刻刻触及我们的生活,更重要的是,还将有我们用以接近和求解问题、管理日常生活、与他人交流和互动的计算概念;而且,面向所有的人,所有地方。当计算思维真正融入人类活动的整体以致不再表现为一种显式之哲学的时候,它就将成为一种现实。






















