
传说,印度的舍罕国王打算重赏国际象棋的发明人——大臣西萨·班·达依尔。这位聪明的大臣跪在国王面前说:“陛下,请你在这张棋盘的第一个小格内,赏给我一粒麦子,在第二个小格内给两粒,在第三个小格内给四粒,照这样下去,每一小格内都比前一小格加一倍。陛下啊,把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧?”国王说:“你的要求不高,会如愿以偿的”。说着,他下令把一袋麦子拿到宝座前,计算麦粒的工作开始了。……还没到第二十小格,袋子已经空了,一袋又一袋的麦子被扛到国王面前来。但是,麦粒数一格接一格地增长得那样迅速,很快看出,即使拿出来全印度的粮食,国王也兑现不了他对象棋发明人许下的语言。国王应给象棋发明人多少粒麦子?
问题的求解可以用求和公式求解:1+2+4+8+……+2^63=2^64-1=18446744073709551615(粒)


算法是指解决问题的方法和步骤。不要把“计算方法”和“算法”这两个词混淆。前者指的是求数值解的近似方法,后者是指解决问题的一步一步的过程。在解一个数值计算问题时,除了要选择合适的计算方法外,还要根据这个计算方法写出如何让计算机一步一步执行以求解的算法。对于计算机外行来说,他们可以只使用别人已设计好的现成算法,只需根据算法的要求给以必要的输入,就能得到输出的结果。对他们来说,算法如同一个“黑箱子”一样,可以不了解“黑箱子”中的结构,只是从外部特性上了解算法的作用,即可方便地使用算法。但对于程序设计人员来说,必须会设计算法,并且根据算法编写程序。

对同一个问题,可以有不同的解题方法和步骤。例如,求1+2+3+…+100,可以先进行1+2,再加3,再加4,一直加到100,也可采取100+(1+99)+(2+98)+…+(49+51)+50=100+50+49×100=5050。还可以有其它的方法。当然,方法有优劣之分。有的方法只需进行很少的步骤,而有些方法则需要较多的步骤。一般说,希望采用方法简单,运算步骤少的方法。因此,为了有效地进行解题,不仅需要保证算法正确,还要考虑算法的质量,选择合适的算法。
瑞士苏黎世大学尼古拉斯·沃斯提出“程序=数据结构+算法”。这个公式对计算机科学的影响程度足以类似物理学中爱因斯坦的“E=MC^2”——一个公式展示出了程序的本质。
算法的要素主要有:
(1)基本操作:算术运算、关系运算、逻辑运算、数据传输。
(2)控制结构:顺序结构、选择结构、循环结构。

尼古拉斯·沃斯
算法的特征是:
(1)有穷性:算法必须在有限个步骤内完成任务。
(2)确定性:算法的描述必须无歧义,以保证算法的实际执行结果是精确地符合要求或期望。
(3)可行性:又称有效性。能够实现,算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。
(4)输入:一个算法必须有零个或以上输入量。
(5)输出:一个算法应有一个或以上输出量,输出量是算法计算的结果。

算法的描述是指对设计出的算法,用一种方式进行详细的描述,以便与人交流。算法可采用多种描述语言来描述,各种描述语言在对问题的描述能力方面存在一定的差异,可以使用自然语言、流程图、伪代码来描述。
(1)自然语言描述
自然语言就是人们日常使用的语言,可以是汉语、英语、或其他语言。用自然语言描述通俗易懂,但文字冗长,容易出现歧义。自然语言表示的含义往往不大严格,要根据上下文才能判断其正确含义。例如,甲队大败乙队。请问是甲队胜了,还是乙队胜了?因此,除了那些简单的问题以外,一般不用自然语言来描述算法。

(2)流程图描述
流程图是用一些图框来表示各种操作。用图形表示算法,直观形象,易于理解。美国标准化协会ANSI(American National Standard Institute)规定了一些常用的流程图符号,已为世界各国程序工作者普遍采用。
| 矩形 —— 处理框 菱形 —— 判断框 平行四边形 —— 输入输出框 圆角矩形 —— 起止框 圆点 —— 连接点
向下或向右箭头 —— 流程线 虚线与左中括号 —— 注释框 | 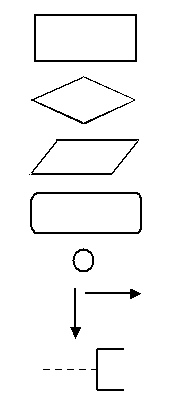
|
(3)伪代码描述
伪代码是用介于自然语言和计算机语言之间的文字和符号来描述算法。它如同一篇文章一样,自上而下地写下来。每一行(或几行)表示一个基本操作。它不用图形符号,因此书写方便,格式紧凑,修改方便,容易看懂,也便于向计算机语言过渡。用伪代码写算法并无固定的、严格的语法规则,可以用英文,也可以中英文混用。只要把意思表达清楚,便于书写和阅读即可,书写的格式要写成清晰易读的形式。
运算符 | 符号表示 | 示例 |
赋值 | ← 或 = | a←5,b=5 |
算术运算 | +、-、*、/、mod(取余)、^乘方 | a+b,a^2 |
关系运算 | >、>=、<、<=、=、<>或!=(不等于) | a mod 2 <> 0 |
逻辑运算 | and(与)、or(或)、not(非) | a>0 and b>0 |
输入输出 | input、output(或 read、write) | input a |
选择结构 | 如果条件P成立,则A,否则B | if a>0 then A else B ---------- if a>0 then A else B endif |
循环结构 | 当型:while P [do] A For型: for i=初值 to 终值 [step n] [do] A | i=1 s=0 while i<=100 do s=s+i i=i+1 endwhile ----------- s=0 for i=1 to 100 [step 1] s=s+i endfor |
数组 | int a[10] | input a i=1 if a[i] mod 2 =0 then output a[i] end if |
函数 | procedure name(参数) ... endprocedure ---------------- function name(参数) return ... endfunction | function max(a,b) if a>b then return a else return b endif endfunction |


















