上课日期：第八周 2020.10.28 3-4节，西校区工程中心204

出勤统计：应到41/实到38/迟到1（鲁良鹏）/请假3（邹瓯铭、陈波、张凯科）

在上一次的课程中，本讲我们重点介绍“马尔科夫决策过程”，用来帮助智能体在随机性任务环境中达到行动合理性。截止目前，人工智能已经具备了一定程度的智能，它可以在确定性环境中完成“最佳搜索”，也可以在非确定性环境中完成“最优决策”，但是，还有一种人类智能，人工智能科学家也希望将它赋能给机器，那就是“推理”能力。例如，在下面的左图中，火星车需要根据传感器获得的信息，对未知环境和状态作出“推理”；右图中，智能体程序需要“推理”被大树所遮挡的环境信息。

如果说，前面课程介绍的“马尔科夫决策过程”是为了帮助智能体在非确定性任务环境中，取得较高的行动合理性；那么，本次课程所要介绍的“贝叶斯网络”，是为了帮助智能体适应部分可观察环境。也就是说，智能体需要根据可观察到的部分状态信息，对不可观察的状态信息作出估计和判断。

 

首先，我们介绍概率图模型。概率图中的节点分为隐含节点和观测节点，边分为有向边和无向边。从概率论的角度，节点对应于随机变量，边对应于随机变量的依赖或相关关系，其中有向边表示单向的依赖，无向边表示相互依赖关系。

 贝叶斯网络（Bayesian Network）和马尔可夫网络（Markov Network）均属于概率图模型。不同之处在于，贝叶斯网络可以用一个有向图结构表示，马尔可夫网络可以表示成一个无向图的网络结构。

 为了理解“贝叶斯网络”，接下来介绍著名的贝叶斯规则。下面，我们看一个具体的例子。某人通过长时间观察，得到以下统计结论。

1）校园内既有男生也有女生，男女生比例为4:6，因此， 性别随机变量Sex表示校园内男生（Male）和女生（Female）的概率。

2）男生和女生中有人留长发，有人留短发，因此，性别随机变量与头发长短随机变量（Sex, Hair）的联合概率分布如下表所示，描述了在不同性别中，出现长发（Long）、短发（Short）的概率。

当观察到一个人留着短发时，请问这个人有多大的可能性为女生。在这个例子中，我们所观察到的统计信息为先验知识，所要解决的问题是，如何根据先验，求解后验知识。以下为求解过程，根据贝叶斯规则，我们可以推断，这个人为女生的概率为0.25。

接下来，我们重点介绍贝叶斯网络。它可以看做是一种数据结构，用于实现概率推理模型。贝叶斯网络是一个有向图，其中每个结点都标注了定量的概率信息。其完整的说明如下：

1. 每个结点对应一个随机变量，这个变量可以是离散的、或者连续的。

2. 一组有向边、或箭头连接结点对。如果有从结点X指向结点Y的箭头,则称X是Y的一个父结点。注意，贝叶斯网络图中没有有向回路。

3. 每个结点X有一个条件概率分布P(X|Parents(X)，用于量化其父结点对该结点的影响。

下面，我们看一个“家用防盗报警器贝叶斯网络”案例，这个报警器对于探测盗贼的闯入是很可靠的，但是偶尔也会对轻微的地震有反应。还有两个邻居John和Mary，他们承诺在你工作时，如果听到警报声就给你打电话。John听到警报声时总是会给你打电话，但是他有时候会把电话铃声当成警报声，然后错误地给你打通了电话。另一方面，Mary特别喜欢大声听音乐，因此，她有时根本听不见警报声，然后就漏掉了给你打电话。这个例子所对应的贝叶斯网络如下图所示。

智能体利用所构造的贝叶斯网络，就具备了推理能力。比如，如果John和Mary都给你打电话，智能体希望推测出有人入室行窃的可能性有多大。

 从语义上分析，一个贝叶斯网络表示多个随机变量的完全联合概率分布，而且满足以下表达式：

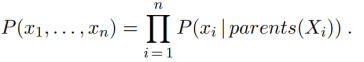利用这个表达式，比如，我们可以计算有盗贼闯入，也没有发生地震，但发生了警报，且John没有打电话，Mary给你打了电话的概率为0.0000656684。可见，这种情况发生的可能性极小。在计算过程中，我们将联合分布中的一些条目概率相乘:

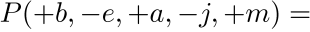
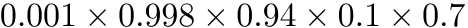
下面，我们看看贝叶斯网络的构建过程：

首先，确定结点。即确定为了对问题域建模所需要的随机变量的集合。注意，变量排序很重要，通常，使原因变量排在结果变量之前，这样得到的网络结构会更紧致。

其次，确定边。依次选定某个节点Xi，从X1,…,Xi-1中选择Xi的父结点的最小集合，在每个父结点与Xi之间插入一条边；最后，写出节点Xi的条件概率表P(Xi|Parents(Xi))。

 在结束本次课程之前，我们介绍，如何有效地写出某个节点Xi的条件概率表P(Xi|Parents(Xi))。对于定性结点，它的取值完全能够由其父结点的取值确定，没有任何不确定性。但是，对于非确定性关系，经常可以用噪声逻辑关系来刻画。典型的的例子是噪声或（noisy-OR）模型关系，它是逻辑或的推广。在命题逻辑中，我们可以说：当Fever（发烧）为真，当且仅当Cold（感冒）、Flue（流感）、或者Malaria（疟疾）为真。噪声或模型不同，它允许每个父

结点引起子结点为真的能力的不确定性，即父结点与子结点之间的因果关系有可能被抑制，因此，病人可能得了感冒却并没有发烧的症状。

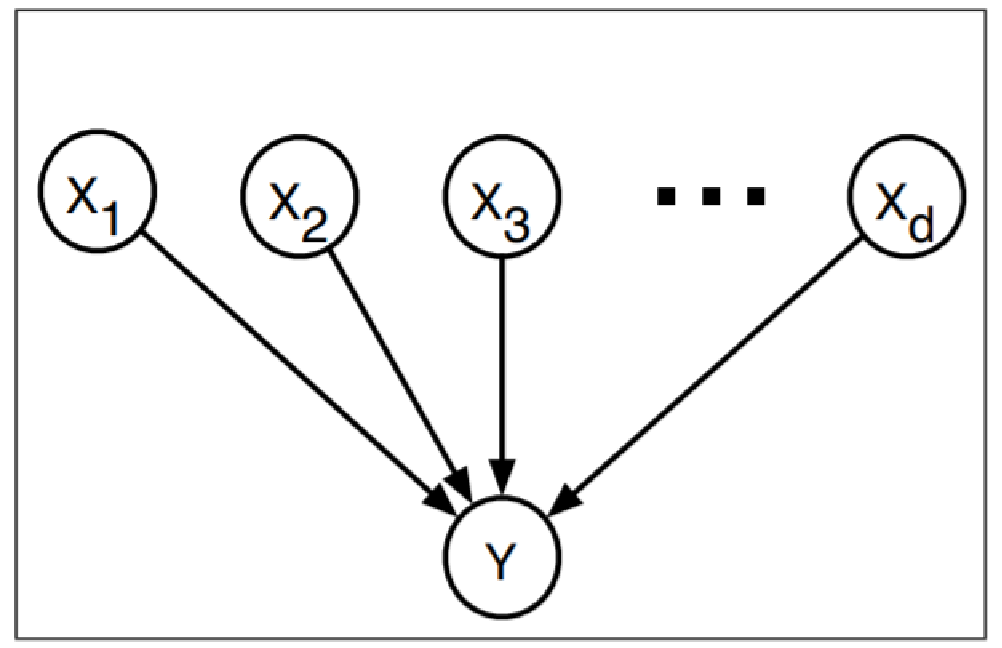
因此，如果某个节点Xi满足噪声或模型，则该节点的条件概率表可使用以下公式进行表达。

其中，

在实际应用中，我们所涉及的贝叶斯网络为“混合贝叶斯网络”，它既包括离散随机变量，也包含联系随机变量。推理方法分为精确推理（exact inference）与近似推理（approximate inference）。