上课日期：第五周 2020.10.10 5-6节（补第五周周四的课），西校区工程中心204

出勤统计：应到41/实到40/迟到0/请假1（罗东华）

在前面的课程中，我们学习了如何利用“搜索”技术实现人工智能中的问题求解，并重点介绍了“盲目搜索”与“知情搜索”中若干经典算法。这类算法存在的一个明显的约束条件，即智能体的任务环境必须满足确定性。

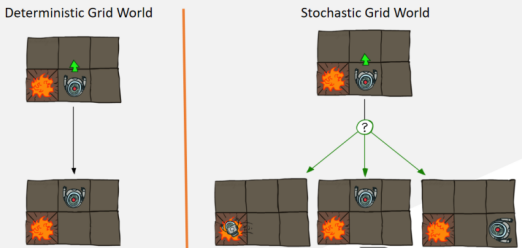
接下来的两次课程中，我们将重点介绍“马尔科夫决策过程”的相关知识，用来帮助智能体在随机性任务环境中达到行动合理性。下面这个例子，很好地解释了什么是“随机性任务环境”。在左图中，机器人的初始状态处于下方中间方格位置，它的左边格子有一个火堆。当它收到“前进”的动作指令后，机器人执行指令并进入上方中间方格位置；这称为“确定性任务环境”。在右图中，机器人具有相同的初始状态，并收到相同的动作指令，但是机器人的后继状态有三种，分别为向左走陷入火堆；向上走进入上方中间方格位置；向右走进入下方右边方格。我们可以看到，虽然机器人的后继状态的概率分布是确定性的，但是单个后继状态满足非确定性，这样的任务算计，我们称之为“随机性任务环境”。

在人工智能中，我们可以利用“马尔科夫过程”来简化由于任务环境的随机性所引发的随机过程（random process）。其简化的基本思路是使得随机过程的状态不具有记忆能力，也就是说，智能体在t+1时刻的状态，只与t时刻的状态和t时刻的动作有关，与t时刻之前的历史没有任何关系，不同时刻状态与状态之间的独立性，我们称为“马尔科夫性”。

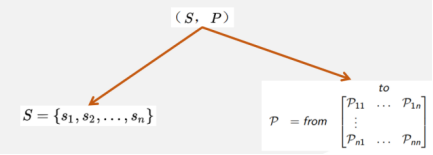
从数学建模的角度看，一个马尔科夫过程可以表示为二元组，如下图所示，S为智能体的状态集合，P为状态转移矩阵，矩阵的每一行的所有值的和为1，描述了某一个状态的后继状态的概率分布。

下图为一个“学习马尔科夫决策过程”：

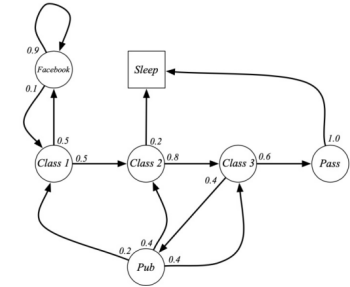
图中，圆圈表示学生所处的状态，方格Sleep是一个终止状态，或者可以描述成自循环的状态，也就是Sleep状态的下一个状态100%的概率还是自己所处的状态。箭头表示状态之间的转移，箭头上的数字表示当前转移的概率。

举例说明：当学生处在第一节课（Class1）时，他有50%的概率会参加第2节课（Class2）；同时在也有50%的概率不在认真听课，而进入到浏览facebook这个状态中。在浏览facebook这个状态时，他有90%的概率在下一时刻继续浏览，也有10%的概率返回到课堂内容上来。当学生进入到第二节课（Class2）时，会有80%的概率继续参加第三节课（Class3），也有20%的概率觉得课程较难，而退出进入（Sleep）状态。当学生处于第三节课这个状态时，他有60%的概率通过考试，继而以100%的概率退出该课程，也有40%的可能性需要到去图书馆之类的地方查找参考文献，此后根据其对课堂内容的理解程度，又分别有20%、40%、40%的可能性返回值第一、第二、第三节课，重新继续学习。

该随机过程的马尔科夫过程可以表示为：

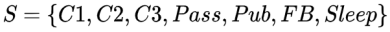
至于马尔科夫链，我们简单地理解为，状态之间满足时序性的马尔科夫过程。

接下来，我们介绍马尔科夫奖励过程。马尔科夫奖励过程在马尔科夫过程的基础上增加了奖励R和衰减系数γ。R是一个奖励函数，描述从一个状态进入下一个状态所能获得的奖励期望。衰减系数γ∈ [0, 1]，它的引入有很多理由。例如，数学表达更方便，避免陷入无限循环，远期利益具有一定的不确定性，符合人类对于眼前利益的追求，符合金融学上获得的利益能够产生新的利益。

在马尔科夫奖励过程中，我们比较关注的是如何计算某个状态下的收益和价值。对于收益的计算，它是在一个马尔科夫奖励链上从t时刻开始，往后所有的奖励的有衰减的总和；其中，衰减系数体现了未来的奖励在当前时刻的价值比例，γ接近0，则表明模型偏重于“近期”的利益；相反，γ接近1，则则表明模型偏重于考虑远期的利益。价值函数给出了某一状态或某一行为的长期价值。在一个马尔科夫奖励过程中，某一状态的价值函数为从该状态开始的马尔可夫链收获的期望。根据著名的Bellman公式，在一个马尔科夫奖励过程中，某一状态的价值函数包括两个部分，第一个部分为从当前状态进入下一个状态的即时奖励，第二个部分为当前状态的所有后继状态的折扣价值的和。

较于马尔科夫奖励过程，马尔科夫决策过程多了一个行为集合A，A表示的是有限的行为的集合。看起来很类似马尔科夫奖励过程，但这里的P和R都与具体的行为a对应，而不像马尔科夫奖励过程那样仅对应于某个状态。在马尔科夫决策过程中，我们关注的是，如何确定最优决策，获得状态的最大价值。一个策略完整定义了个体的行为方式，也就是说定义了个体在各个状态下，各种可能的行为方式以及其概率的大小。策略仅和当前的状态有关，与历史信息无关；同时，某一确定的策略是静态的，与时间无关；但是个体可以随着时间更新策略。

This course mainly discusses the general problem of representing and reasoning about probabilistic temporal processes.

First , the changing state of the world is handled by using a set of random variables to represent the state at each point in time.

Second,  representations can be designed to satisfy the Markov property, so that the future

is independent of the past given the present. Combined with the assumption that the

process is stationary—that is, the dynamics do not change over time—this greatly

simplifies the representation.