授课日期：第三周 2020-9-24，下午5-6，西校区工程中心204教室

出勤统计：应到41/实到41/迟到4人

利用“抽象”原理，尽可能低忽略与问题和环境任务相关的细节，基于目标的智能体可以轻松地转换为设计合适的“问题求解器（problem-solving）”。为了便于实现，科学家提出了“问题形式化”技术，使得问题求解器的设计问题转换为“树搜索”问题。

在上一次的讲课中，我们以“搜索”为例子，介绍了问题求解的相关知识，包括问题形式化方法、搜索算法的分类，以及评估搜索智能体合理性的四个重要维度，即时间复杂度、空间复杂度、完备性和最优性。

本讲我们重点介绍“盲目搜索”中比较经典的搜索策略。

首先，我们需要学习的第一个知识点是“树搜索”，在英文中，我们称之为“tree-search”。这样做的目的是，可以利用“树”这种独特的数据结构，协助、记录整个搜索过程。下面这张图显示了，我们如何将问题形式化后，所得到的、由初始状态、动作集合、状态转移模型所构成的状态空间图，转换为适用于“树搜索”的树形数据结构。

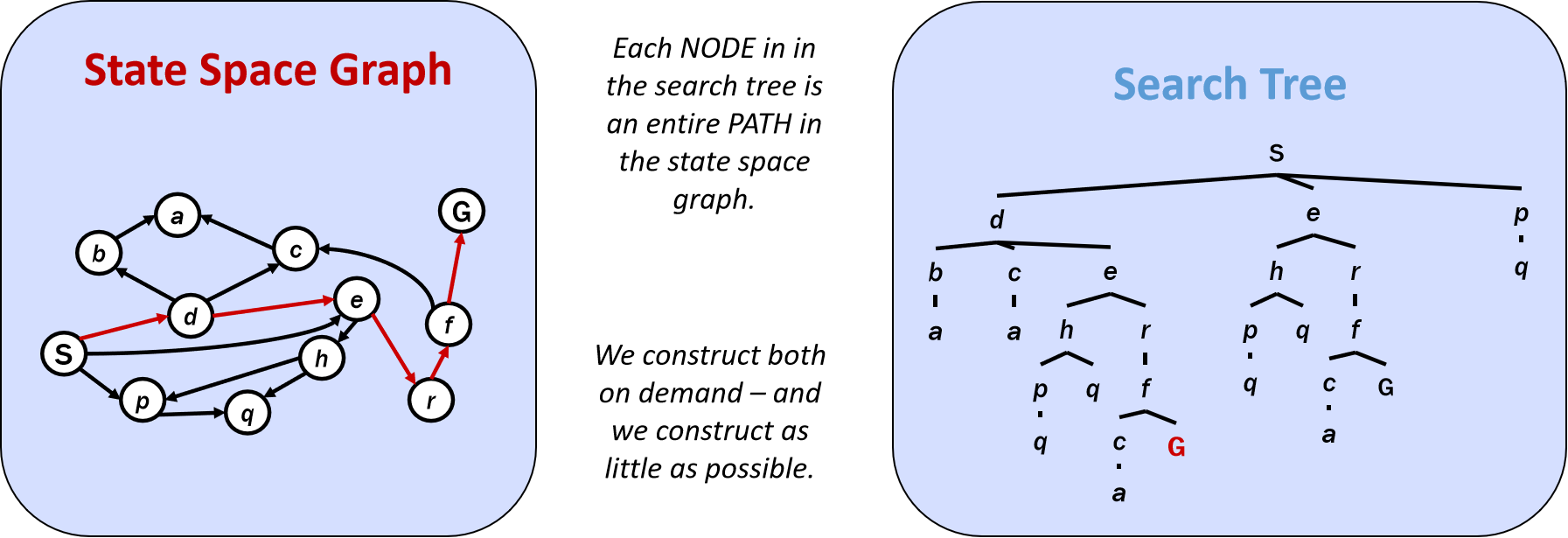
1. 状态空间图中的初始状态，以“搜索树”的根节点进行表示；

2. 状态空间图中的初始状态动作集合，以“搜索树”的“父节点-子节点”之间的相连边进行表示。

3. 状态空间图中的状态转移模型，以“搜索树”的后继节点进行表示。

因此，智能体在某一状态下，意味着智能体处在“搜索树”中对应的某一节点。在任一给定节点，所有待扩展的结点的集合称为边缘、或者开集。在开集中选择不同的节点，意味着智能体采取了不同的搜索策略。 

其次，我们需要搞清楚，“树搜索”与“图搜索”的差异。两者的相似之处是，都采用了树形数据结构。不同之处是，“图搜索”除了需要利用队列管理开集之外，还需要利用队列管理访问历史。这个管理历史的队列，我们称为探索集、或者闭集。也就是说，探索集管理搜索过程中，曾经访问过的树节点。这样做的好处是，可以避免问题求解中，出现有环路径或冗余路径。在基于目标的智能体设计中，有环路径或冗余路径会破坏智能体的合理性。

这张图，可以清晰地看到“树搜索”与“图搜索”这两类算法的差异性。图中红色方框表示的是“图搜索”所增加使用的探索集。

最后，我们看几类经典的“盲目搜索”算法。

1. 广度优先搜索

这是一种简单的搜索策略，先扩展根结点，接着扩展根结点的所有后继，然后再扩展其它开集的的后继，依此类推。一般地，在下一层的任何结点扩展之前，搜索树上较低深度，或者具有相同深度的所有结点都应该已经扩展过。

2. 深度优先搜索

这种搜索策略总是扩展搜索树的开集中最深的结点。搜索过程可以很快推进到搜索树的最深层，直到那里的结点没有后继。当那些结点扩展完之后，就从边缘结点集中去掉，然后搜索算法回溯到下一个还有未扩展后继的深度稍浅的结点。

3. 受限深度优先搜索

在无限状态空间内，深度优先搜索会令人尴尬地失败，而这个问题可以通过对深度优先搜索设置界限来避免。就是说，深度达到界限的结点，被当作没有后继对待。这种方法称为受限深度优先搜索。深度界限解决了无穷路径的问题。

4. 迭代深度优先搜索

迭代深度优先搜索是一种常用策略，它经常和深度优先搜索结合使用，来确定最好的深度界限。做法是不断地增大深度的界限阈值。首先为0，接着为1，然后为2，依此类推，直到找到目标。

5. 代价敏感的一致代价搜索。

代价敏感的一致代价搜索是盲目搜索中一种代价敏感型算法。与单个广度优先搜索、深度优先搜索算法不同，它充分利用了来自问题形式化本身的路径代价信息，使得其具备广度优先搜索算法的完备性和最优性；同时具备类似深度优先搜索算法较低的空间复杂度。

在结束本讲之前，同学们需要知道，不同的搜索算法，对应着不同的搜索策略，智能体程序的算法实现也不同。广度优先搜索的开集采用先进先出的队列，即First in first out queue；深度优先搜索及其变种算法采用先进后出的队列，即first in last out queue；代价敏感的一致代价搜索采用优先级队列，即priority-based queue。

This course mainly discusses about the tree-search and graph-search. We need to keep in mind that how a state space graph is converted into a search tree. Also, the difference between tree-search and graph-search is mainly due to the data structure, called closed set or explored set, newly introduced by graph-search.

For uninformed search methods, the basic algorithms are as follows:

First, breadth-first search expands the shallowest nodes first; it is complete, optimal for unit step costs, but has exponential space complexity.

Second, depth-first search expands the deepest unexpanded node first. It is neither complete nor optimal, but has linear space complexity.

Third, depth-limited search adds a depth bound.

Forth, iterative deepening search calls depth-first search with increasing depth limits until a goal is found. It is complete, optimal for unit step costs, has time complexity comparable to breadth-first search, and has linear space complexity.

Last, uniform-cost search expands the node with lowest path cost, g(n), and is optimal for general step costs.