授课日期：第三周 2020-9-23，上午3-4，西校区工程中心204教室

出勤统计：应到41/实到40/迟到0

通过上周课程的学习，我们了解到，人工智能技术的主要任务可归结为如何设计智能体（intelligent agent design），而智能体最基本的特质是理性（rationality）。从技术发展的脉络看，智能体可分为四类，分别为简单反射智能体（simple reflex agents）、基于模型智能体（model-based agents）、基于目标智能体（goal-based agents）和基于效用智能体（utility-based agents）。

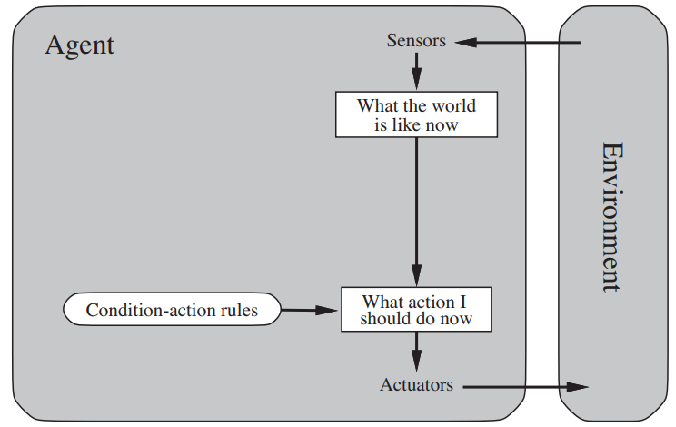
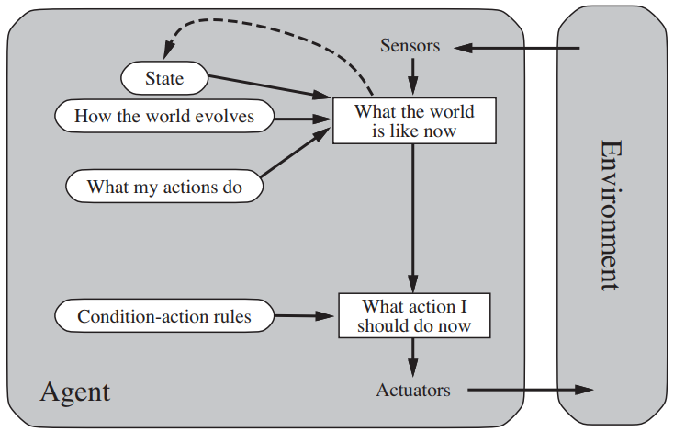
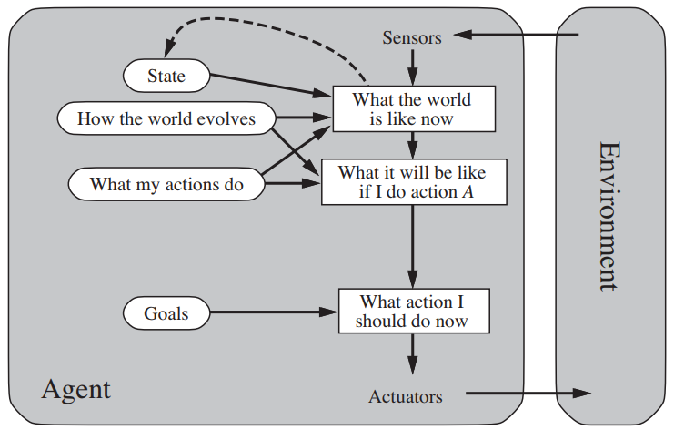
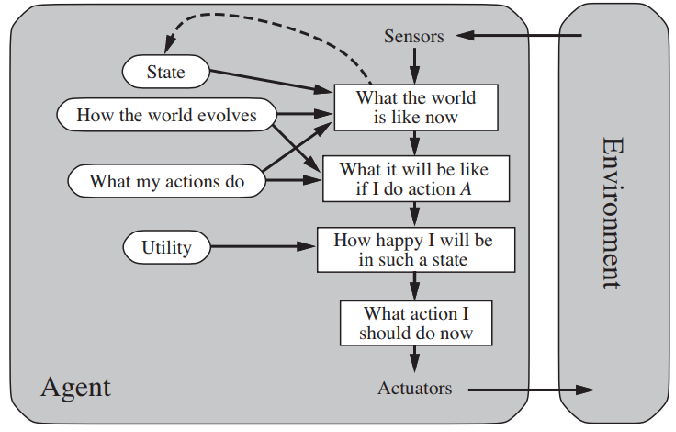
在上一次的讲课中，我们通过“真空吸尘器”的例子，已经了解了什么是“理性”的智能体，以及如何评估一个智能体是否理性。

本讲我们以搜索为例子，具体讲解基于目标的智能体，在进行问题求解时，该如何保持行动的合理性。

“搜索”可以简单地理解为，在一个给定的状态空间中，从一个“起始状态”出发，通过智能体程序算法，最终到达“目标状态”。寻找从“起始状态”到“目标状态”的可行路径的过程，我们称为问题的求解。

下面是罗马尼亚的一张城市地图，地图上显示了各个城市之间的相邻关系，以及相邻城市之间的距离。假如你是一个人工智能工程师，正在参与导航软件的研发。当用户输入从Arad这个城市出发，前往Bucharest目的城市时，你的导航智能体应该如何工作，给出合理的建议呢？

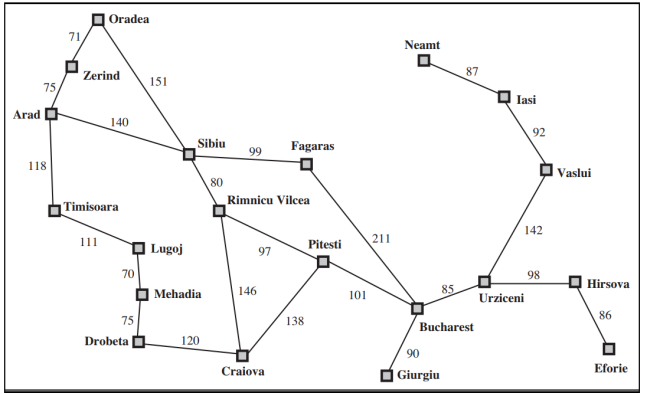
你要做的第一件事情是，对待求解的问题进行形式化。在英文里，我们称为problem formulation。我们以“罗马尼亚导航”问题为例，介绍问题形式化的详细步骤。通常，问题形式化包括五个部分：

1. 确定智能体的初始状态。例如，在“罗马尼亚导航”问题中，Agent的初始状态可以描述为In(Arad)。

2. 描述Agent的可能行动。给定一个状态s，ACTIONS(s)返回在状态s下，可以执行的动作集合。因此，我们称这些行动对状态s而言是可应用的。例如，考虑初始状态In(Arad)，可应用的行动集合为: {Go(Sibiu)，Go(Timisoara)，Go(Zerind)}

3. 制定状态的转移模型。转移模型可以用函数 RESULT(s, a）描述，也就是，在状态s下，执行行动a后达到的状态，称为在转移模型作用下，动作的行动结果。我们通常使用术语“后继状态”，来表示从一给定状态出发，通过单步行动可以到达的状态集合。例如，RESULT(In(Arad)，Go(Zerind))=In(Zerind)

4. 目标测试。也就是，测试一个给定的状态是否属于目标状态。有时候，目标状态是一个显式集合。这个时候，目标测试只需简单检查给定的状态是否在目标状态集合中。在“罗马尼亚导航”问题中，目标状态集合是一个单元素集合{In(Bucharest)}。有些时候，目标状态并不是一个显式的、可枚举的目标状态集合，而是具备某些特定抽象属性的状态。例如，在象棋游戏中，目标状态是指对方被“将死”，即对方的国王在己方的攻击下，已经无路可逃，必死无疑。

5. 路径代价测试。我们可用代价函数，为每条路径赋一个代价值，即边加权值。问题求解 Agent选择能反映它自己的性能度量的代价函数。在“罗马尼亚导航”问题中，对于试图前往 Bucharest 的Agent，时间是基本要素，所以，它的路径代价可以是的路径的长度。

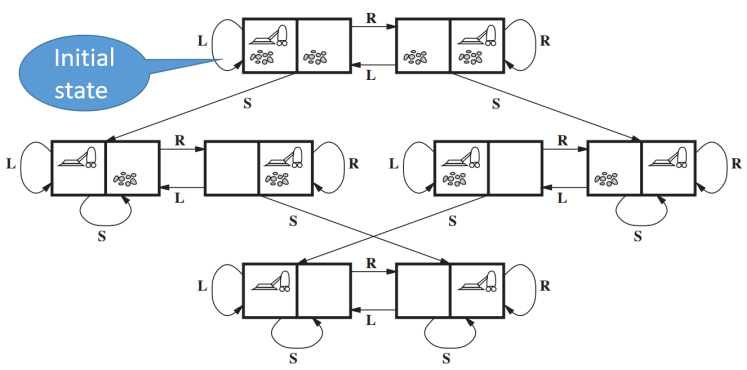
到此，关于问题形式化的所有技巧我们介绍完了。这面这张图是“真空吸尘器”智能体的状态空间。它包括了问题形式化中的前三项，分别为初始状态、可能的行动，以及动作转移模型。

在完成问题形式化后，我们要做的第二件工作时，实现智能体程序。在本讲的搜索例子中，搜索算法分为两类，分别为盲目搜索、知情搜索。

盲目搜索也叫无信息搜索，指的是算法仅仅利用了问题形式定义中提供的信息，搜索算法要做的是生成后继并区分目标状态与非目标状态。盲目搜索策略是以状态结点扩展的次序来分类的，常见的搜索策略包括广度优先搜索、深度优先搜索、深度受限搜索、迭代深度搜索，以及代价敏感的一致代价搜索。

知情搜素（Informed search）又称为启发式搜素（Heuristic search），这类算法在搜素策略中运用了若干与问题形式化（Problem formulation）本身之外的、被认可的知识（Knowledge）或经验（Experience），从而加速搜索算法的计算和目标收敛。

在结束本讲之前，同学们需要知道，在搜索问题中，智能体的合理性通过四个方面进行评估，分别为智能体程序算法的时间复杂度、空间复杂度、完备性和最优性。

1. 时间复杂度:找到解需要花费多长时间?

2. 空间复杂度:在执行搜索的过程中需要多少内存?

3. 完备性:当问题有解时,这个算法是否能保证找到解?

4. 最优性:搜索策略是否能问题形式化定义中的最优解?

时间和空间复杂度通常要与问题的难度规模一起考虑。在理论计算机科学中，一种典型的度量方式是状态空间图的大小。在AI领域，状态空间图大多由初始状态、行动和转移模型来隐式表示，并且大多是无限的。因此，复杂度通常由下列三个量来表达，分别为分支因子，或者说任何结点的最多后继数；目标结点所在的最浅的深度；状态空间中任何路径的最大长度。时间常常由搜索过程中产生的结点数目来度量,而空间则由在内存中储存的最多结点数来度量。

This course mainly discusses about the problem formulation in problem-solving, and how to evaluate the rationality of search agents.

First, before an agent can start searching for solutions, a goal must be identified and a welldefined problem must be formulated.

Second, a problem consists of five parts: the initial state, a set of actions, a transition model describing the results of those actions, a goal test function, and a path cost function.

Third, the environment of the problem is represented by a state space. A path through the state space from the initial state to a goal state is a solution.

Forth, search algorithms treat states and actions as atomic: they do not consider any internal structure they might possess.

Fifth, search agent algorithms are judged on the basis of completeness, optimality, time complexity, and space complexity. Complexity depends on the branching factor in the state space, and the depth of the shallowest solution target.

Last, Uninformed search methods have access only to the problem definition, while informed search methods may have access to a heuristic function h(n) that estimates the cost of a solution from a given state.