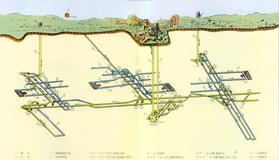
第四节  能量方程在矿井通风中的应用

一、水平风道的通风能量（压力）坡度线

 1、 能量（压力）坡度线的作法 

意义：掌握压力沿程变化情况；有利于通风管理。

如图所示的通风机－水平风道系统，绘制能量（压力）坡度线。

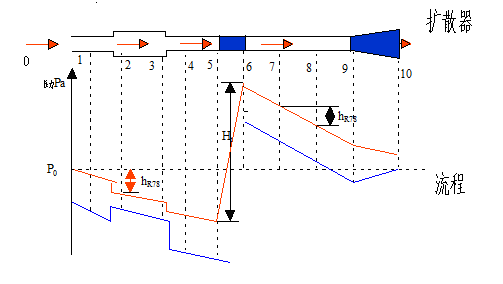
 （1）风流的边界条件

 入口断面处：风流入口断面处的绝对全压等于大气压（可用能量方程加以证明，对入口断面的内外侧列能量方程并忽略极小的入口流动损失），即：

       ，所以，，；

 出口断面处 ：风流出口断面处的绝对静压等于大气压（可用能量方程加以证明，对出口断面的内外侧列能量方程并忽略极小的出口流动损失），即：

     ，所以，，；

 （2）作图步骤

 １）、以纵坐标为压力（相对压力或绝对压力），横坐标为风流流程。

 ２）、根据边界条件确定起始点位置。

 ３）、将各测点的相对静压和相对全压与其流程的关系描绘在坐标

 ４）、最后将图上的同名参数点用直线或曲线连接起来，就得到所要绘制的能量（压力）坡度线。

 2、 能量（压力）坡度线的分析

（1）通风阻力与能量（压力）坡度线的关系

 由于风道是水平的，故各断面间无位能差，且大气压相等。由能量方程知，任意两断面间的通风阻力就等于两断面的全压差：

 （∵）

 1） 抽出段  求入口断面至i断面的通风阻力，由上式得：

     （）

 即：入口至任意断面i的通风阻力（）就等于该断面的相对全压（）的绝对值。

 求负压段任意两断面（ 、）的通风阻力：

 ∵　  又∵

 同理：

 ∴

       

若     h_Ri～j＝ | h_j |－ | h_i |

2）压入段 求任意断面i至出口的通风阻力，由上式得：

h_Ri～10  = h_ti － h_t10 =  h_ti－ h_v10 (h₁₀=0）          

 即：压入段任意断面i至出口的通风阻力（h_Ri～10）等于该断面的相对全压（h_ti）减去出口断面的动压（h_v10） 。

 求正压段任意两断面（i 、j ）的通风阻力：

 同理可推导两断面之间的通风阻力为：

              h_Rij ＝ h_ti－h_tj

（2）能量（压力）坡度线直观明了地表达了风流流动过程中的能量变化。

 绝对全压（相对全压）沿程是逐渐减小的；

 绝对静压（相对静压）沿程分布是随动压的大小变化而变化。

(3扩散器回收动能（相对静压为负值）

 所谓扩散器回收动能，就是在风流出口加设一段断面逐渐扩大的风道，使得出口风速变小，从而达到减小流入大气的风流动能。扩散器安设的是否合理，可用回收的动能值（h_v）与扩散器自身的通风阻力（h_Rd）相比较来确定，即：

      h_v=h_vex－h_vex’h_Rd    合理

      h_v= h_vex－h_vex’< h_Rd   不合理

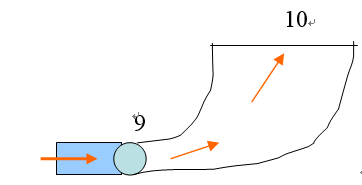
  在压入段出现相对静压为负值的现象分析，

 如上图，对 9 ～10 段列能量方程：

 h_R9～10 =(P₉＋h_v9)－( P₁₀+ h_v10)=P₉＋h_v9－P₀－h_v10

            = h₉＋h_v9－h_v10

    ∴h₉ = h_R9～10－（h_v9－h_v10）

如果：h_v9－h_v10 > h_R9～10，则， h₉<0  （为负值） 

 因此，测定扩散器中的相对静值就可判断扩散器的安装是否合理，相对静压的负值越大，其扩散器回收动能的效果越好。

（三）、通风机全压（H_t）

 1、通风机全压的概念

 通风机的作用：就是将电能转换为风流的机械能，促使风流流动。通风机的全压Ht等于通风机出口全压与入口全压之差：

H_t=  P_t6－P_t5

 2、通风机全压Ht与风道通风阻力、出口动能损失的关系

  由能量方程和能量（压力）坡度线可以看出：

 h_R6～10 =P_t6－P_t10    ∴P_t6 = h_R6～10＋P_t10，

       h_R0～5 = P_t0－P_t5    ∴ P_t5 = P_t0－h_R0～5，

 H_t = P_t6－P_t5 = h_R6～10＋P_t10－（P_{t 0}－h_R0～5）

   =h_R6～10＋P₀＋h_v10－（P₀－h_R0～5）=h_R6～10＋h_v10＋h_R0～5

   H_t= h_R0～10＋h_v10

 ∴ 通风机全压是用以克服风道通风阻力和出口动能损失。

通风机用于克服风道阻力的那一部分能量叫通风机的静压Hs。

H_s= h_R0～10,      H_t= H_s ＋h_v10

两个特例：

a）、无正压通风段（ 6断面直接通大气）

通风机全压仍为：H_t =  P_t6－P_t5

∵P_t5=P_t０－h_R０～5；P_t6= P₀＋h_v6

∴ H_t= h_R０～5＋h_v6

b）、无负压通风段（５断面直接通大气）

      ∵P_t6=h_R6～10＋P_t10，P_t10=P₀＋h_v10；P_t5=P₀

 ∴H_t=h_R6～10＋h_v10

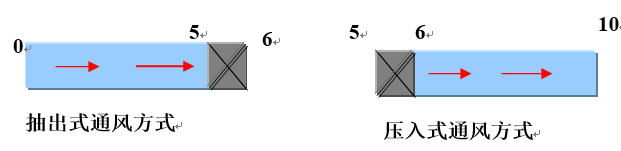
 无论通风机作何种工作方式，通风机的全压都是用于克服风道的通风阻力和出口动能损失；其中通风机静压用于克服风道的通风阻力。

二、通风系统风流能量（压力）坡度线

(一) 通风系统风流能量（压力）坡度线

 绘制矿井通风系统的能量（压力）坡度线(一般用绝对压力)的方法：是沿风流流程布设若干测点，测出各点的绝对静压、风速、温度、湿度、标高等参数，计算出各点的动压、位能和总能量；然后在压力（纵坐标）－－ 风流流程（横坐标）坐标图上描出各测点，将同名参数点用折线连接起来，即是所要绘制的通风系统风流能量（压力）坡度线。

 以下图所示简化通风系统为例，说明矿井通风系统中有高度变化的风流路线上能量(压力)坡度线的画法。

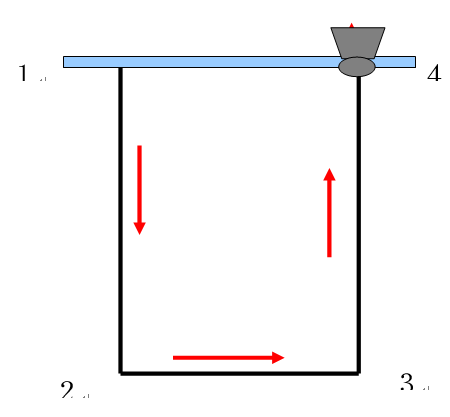
 作图步骤：

 1. 确定基准面。一般地，以最低水平(如2-3)为基准面。

 2. 测算出各断面的总压能(包括静压、动压和相对基准面的位能)。

 3. 选择坐标系和适当的比例。以压能为纵坐标，风流流程为横坐标，把各断面的静压、动压和位能描在坐标系中，即得1、2、3、4断面的总能量。

 4. 把各断面的同名参数点用折线连接起来，即得1－２－３－４流程上的压力坡度线。

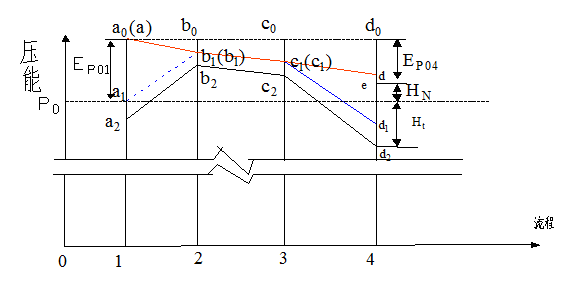
(二) 矿井通风系统能量（压力）坡度线的分析

 1、能量（压力）坡度线（ a-b-c-d ）清楚地反映了风流在流动过程中，沿程各断面上全能量与通风阻力h_R之间的关系。

 全能量沿程逐渐下降，从入风口至某断面的通风阻力就等于该断面上全能量的下降值（如b₀b），任意两断面间的通风阻力等于这两个断面全能量下降值的差。

 2、绝对全压和绝对静压坡度线的坡度线变化有起伏（如1~2段风流由上向下流动，位能逐渐减小，静压逐渐增大；在3~4段其压力坡度线变化正好相反，静压逐渐减小，位能逐渐增大）。说明，静压和位能之间可以相互转化。

 3、1、４断面的位能差(E_P01-E_P04)叫做自然风压(H_N)。H_N和通风机全压（H_t)共同克服矿井通风阻力和出口动能损失。

          H_N+H_t(d_2~e)=(d₀~d)+(d₁~d₂)

 ４、能量（压力）坡度线可以清楚的看到风流沿程各种能量的变化情况。特别是在复杂通风网络中，利用能量（压力）坡度线可以直观地比较任意两点间的能量大小，判断风流方向。这对分析研究局部系统的均压防灭火和控制瓦斯涌出是有力的工具。（例见Ｐ３３）

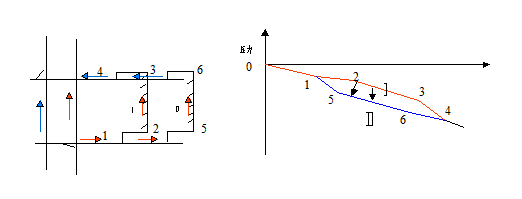
例2  如图2-4-4所示的同采工作面简化系统，风流从进风上山经绕道1分为二路；一路流经1－２－３－４(2－３为工作面Ⅰ)；另一路流经１－５－６－４（５－６为工作面Ⅱ）。两路风流在回风巷汇合后进入回风上山。如果某一工作面或其采空区出现有害气体是否会影响另一工作面？

解：要回答这一问题，可以借助压力坡度线来进行分析。为了绘制压力坡度线，必须对该局部系统进行有关的测定。根据系统特点，沿风流流经的两条路线分别布置测点，测算出各点的总压能。根据测算的结果即可绘出压力坡度线见图2-4-5。由压力坡度线可见，1－２－３－４线路上各点风流的全能量大于１－５－６－４线路上各对应点风流的全能量。所以工作面Ⅰ通过其采空区向工作面Ⅱ漏风，如果工作面Ⅰ或其采空区发生火灾时其有害气体将会流向工作面Ⅱ，影响工作面Ⅱ的安全生产。

三、通风系统网络相对压能图和相对等熵静压图

 对于较复杂的通风系统，由于井巷分支多，结构复杂，用压力坡度线表示就会出现坡度线相互交错，给使用带来不便。为此提出了使用通风系统网络相对压能图或相对等熵静压图。

 实质：就是节点赋于压能值的通风系统网络图。压能图各节点的压能值是相对于某一基准面所具有的总能量值；或是相对某一参考面（如进风井口等）之间的通风阻力。

 压能图的绘制与能量（压力）坡度线的绘制基本相同。

 波兰学者提出了用相对等熵静压图来表示通风系统中风流各点的能位关系，因为某一节点的相对静压h_i  = P_i-P_0i ，而井巷风流的 P_0i  未知。假设大气压随高度变化属理想的绝热等熵过程，根据气态方程可推算P_0i ，记为  P_i 。

 只要实测出通风系统中风流i点的绝对静压Pi，它与对应高度的等熵静压之差就是相对等熵静：

 以相对等熵静压为纵坐标，横坐标无标量，按通风系统结构布置，即可画出相对等熵静压图。