第三节    矿井通风中的能量方程

 当空气在井巷中流动时，将会受到通风阻力的作用，消耗其能量；为保证空气连续不断地流动，就必需有通风动力对空气作功，使得通风阻力和通风动力相平衡。

 一、空气流动连续性方程

 在矿井巷道中流动的风流是连续不断的介质，充满它所流经的空间。在无点源或点汇存在时，根据质量守恒定律：对于稳定流，流入某空间的流体质量必然等于流出其的流体质量。

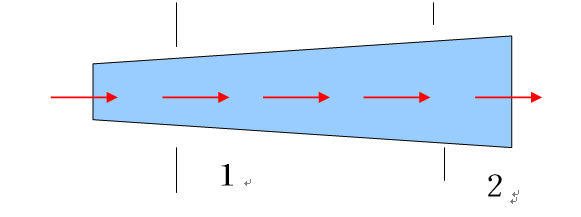
 如图井巷中风流从1断面流向2 断面，作定常流动时，有：

                   Mi=const

                           

     、－－1、2断面上空气的平均密度，kg/m³ ；                                 

    、－－1、2  断面上空气的平均流速，m/s；

    、－－  1、２断面面积，m²。

 两种特例：

 （I） 若＝，则＝； 

 （II）若＝_，则＝。

 对于不可压缩流体，通过任一断面的体积流量相等，即                                      

 二、可压缩流体的能量方程

 能量方程表达了空气在流动过程中的压能、动能和位能的变化规律，是能量守恒和转换定律在矿井通风中的应用。

 （一）、单位质量(1kg)流量的能量方程

 在井巷通风中，风流的能量由机械能（静压能、动压能、位能）和内能组成，常用1kg空气或1m³空气所具有的能量表示。

 机械能：静压能、动压能和位能之和。

 内能：风流内部所具有的分子内动能与分子位能之和。空气的内能是空气状态参数的函数，即：u  = f（ T，P）。能量分析

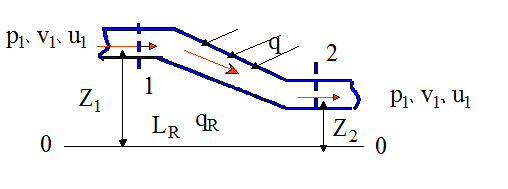
  任一断面风流总机械能：压能＋动能＋位能

  任一断面风流总能量：压能＋动能＋位能＋内能，

 所以，对单位质量流体有：

  1-1断面的总能量：

  2-2断面的总能量：

 假设：1kg空气由1 断面流至2 断面的过程中， L_R（J/kg）：克服流动阻力消耗的能量;q_R（J/kg）：LR  部分转化的热量(这部分被消耗的能量将转化成热能仍存在于空气中）；q（J/kg）：外界传递给风流的热量（岩石、机电设备等）。根据能量守恒定律：

 根据热力学第一定律，传给空气的热量（q_R+q），一部分用于增加空气的内能，一部分使空气膨胀对外作功，即：

式中：v为空气的比容，m³/kg。又因为：

 上述三式整理得：

即为：单位质量可压缩空气在无压源的井巷中流动时能量方程的一般形式。

 式中

 称为伯努力积分项，它反映了风流从1断面流至2断面的过程中的静压能变化，它与空气流动过程的状态密切相关。对于不同的状态过程，其积分结果是不同的。

 对于多变过程，过程指数为n  ，对伯努利积分进行积分计算，可得到：单位质量可压缩空气在无压源的井巷中流动时能量方程可写成如下一般形式。

其中过程指数n按下式计算：

 有压源 Lt 在时，单位质量可压缩空气井巷中流动时能量方程可写成如下一般形式。

令

式中m表示1，2断面间按状态过程考虑的空气平均密度，得

则单位质量流量的能量方程式又可写为

                        

（二）、单位体积(1m3)流量的能量方程

 我国矿井通风中习惯使用单位体积（1m³）流体的能量方程。在考虑空气的可压缩性时，那么1m³  空气流动过程中的能量损失（h_R，J/m³（Pa），即通风阻力）可由1kg空气流动过程中的能量损失（LR J/Kg）乘以按流动过程状态考虑计算的空气密度ρ_m，即：h_R=L_R.ρ_m；则单位体积(1m³)流量的能量方程的书写形式为：

  几点说明：1、1m³  空气在流动过程中的能量损失（通风阻力）等于两断面间的机械能差。

 2、gρ_m（Z₁-Z₂）是1、2  断面的位能差。当1、2 断面的标高差较大的情况下，该项数值在方程中往往占有很大的比重，必须准确测算。其中，关键是ρ_m的计算，及基准面的选取。

 ρ_m的测算原则：将1－2测段分为若干段，计算各测定断面的空气密度(测定 P、t 、φ)，求其几何平均值。

  基准面选取：取测段之间的最低标高作为基准面。

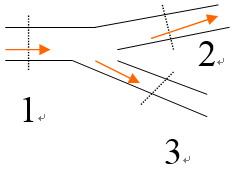
 例如：如图所示的通风系统，如要求1、2断面的位能差，基准面可选在2的位置。其位能差为：

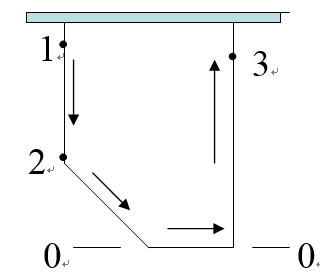
而要求1、3两断面的位能差，其基准面应选在0-0位置。其位能差为：

３、

是1、2两断面上的动能差

 A、 在矿井通风中，因其动能差较小，故在实际应用时，式中可分别用各自断面上的密度代替计算其动能差。即上式写成：

其中：ρ１、ρ2分别为1、２断面风流的平均气密度。

B、动能系数：是断面实际总动能与用断面平均风速计算出的总动能的比。即：

 因为能量方程式中的v₁、v₂分别为1、2断面上的平均风速。由于井巷断面上风速分布的不均匀性，用断面平均风速计算出来的断面总动能与断面实际总动能不等。需用动能系数Kv加以修正。在矿井条件下，Kv一般为1.02～1.05。由于动能差项很小，在应用能量方程时，可取Kv为1。

 因此，在进行了上述两项简化处理后，单位体积流体的能量方程可近似的写成：

或

（三）、关于能量方程使用的几点说明

 1. 能量方程的意义是，表示1kg（或1m³）空气由1断面流向2断面的过程中所消耗的能量（通风阻力），等于流经1、2断面间空气总机械能（静压能、动压能和位能）的变化量。

 2. 风流流动必须是稳定流，即断面上的参数不随时间的变化而变化；所研究的始、末断面要选在缓变流场上。

 3. 风流总是从总能量（机械能）大的地方流向总能量小的地方。在判断风流方向时，应用始末两断面上的总能量来进行，而不能只看其中的某一项。如不知风流方向，列能量方程时，应先假设风流方向，如果计算出的能量损失（通风阻力）为正，说明风流方向假设正确；如果为负，则风流方与假设相反。

 4. 正确选择求位能时的基准面。

 5. 在始、末断面间有压源时，压源的作用方向与风流的方向一致，压源为正，说明压源对风流做功；如果两者方向相反，压源为负，则压源成为通风阻力。

 ６. 应用能量方程时要注意各项单位的一致性。

 7、对于流动过程中流量发生变化，则按总能量守恒与转换定律列方程

 例 1、 在某一通风井巷中，测得1、2两断面的绝对静压分别为101324.7 Pa和101858 Pa，若S₁=S₂，两断面间的高差Z₁-Z₂=100米，巷道中m₁₂=1.2kg/m³，求：1、2两断面间的通风阻力，并判断风流方向。

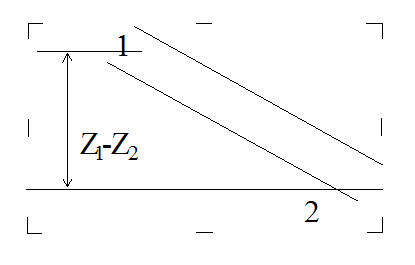
解：假设风流方向12，列能量方程：                                         

=（101324.7－101858）＋0＋100×9.81×1.2

=  643.9  J/m3。

 由于阻力值为正，所以原假设风流方向正确，1→2。

 例 2、在进风上山中测得1、2两断面的有关参数，绝对静压=106657.6Pa，=101324.72Pa；标高差=－400m；气温=15℃，=20℃；空气的相对湿度1=70%,2=80%；断面平均风速=5.5m/s，=5m/s；求通风阻力、。

 解：查饱和蒸汽表得；t₁=15℃时，P_S1=1704Pa；t₂=20℃时，P_S2=2337Pa；

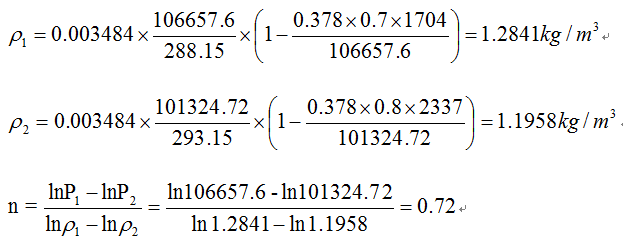
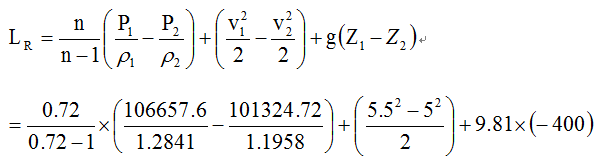
= 382.26 J/kg

   又  

= 1.23877    kg/m3

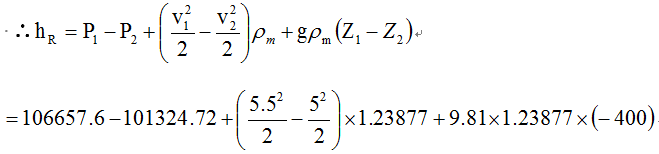
= 475.19  J/m3

或  h_R=L_R×m=382.26×1.23877=  473.53 J/m³。