3.1  栈

3.1.1  栈的定义

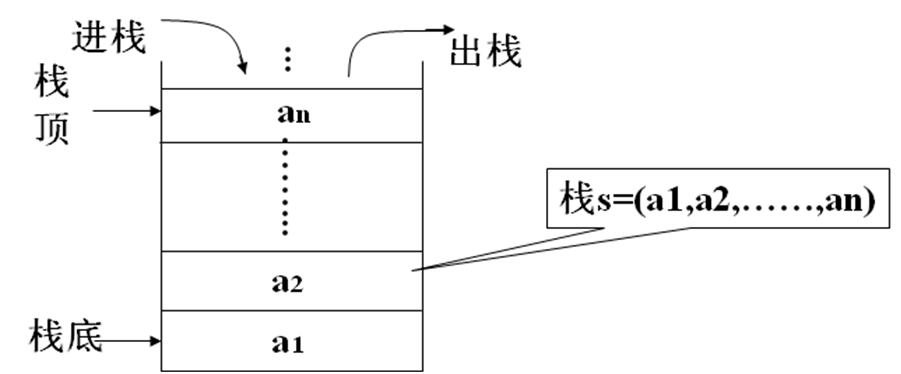
栈是限定仅在表尾进行插入或删除的线性表。允许插入、删除的这一端，即表尾称为栈顶，表的另一端称为栈底。当表中没有元素时称为空栈。如图3.1所示栈中有n个元素，进栈的顺序是a₁、a₂……a_n，当需要出栈时其顺序为a_n、a_n-1……a₁，所以栈又称为后进先出的线性表（Last In First Out），简称 LIFO表。

在日常生活中，有很多后进先出的例子，如食堂里的盘子，在叠放时是从下到上，从大到小，在取盘子时，则是从上到下，从小到大。在程序设计中，常常需要栈这样的数据结构，使得与保存数据时相反顺序来使用这些数据，这时就需要用一个栈来实现。

抽象数据类型栈的定义如下：

ADT Stack { 

数据对象：

D＝{ a_i | a_i ∈ElemSet, i=1,2,...,n,  n≥0 }  {称 n 为栈的长度; 称 n=0 时的栈为空栈。} 

数据关系：

R1＝{ <a_i-1 ,a_i >|a_i-1 ,a_i∈D,  i=2,...,n }   {设栈为 (a₁，a₂,  . . . ，a_i，. . . ，a_n), 称 i 为 a_i 在栈中的位序。}

基本操作：

（1）Init_Stack(s)

初始条件：栈s不存在

操作结果：构造了一个空栈。

（2）Empty_Stack(s)

初始条件：栈s已存在

操作结果：若s为空栈返回为1，否则返回为0。

（3）Push (s，x)

初始条件：栈s已存在                                

操作结果：在栈s的顶部插入一个新元素x， x成为新的栈顶元素。栈发生变化。

（4）Pop (s)

初始条件：栈s存在且非空

操作结果：栈s的顶部元素从栈中删除，栈中少了一个元素。栈发生变化。

（5）Top_Stack(s)

初始条件：栈s存在且非空

操作结果：栈顶元素作为结果返回，栈不变化。

……

} ADT Stack

3.1.2  顺序栈的存储结构和操作的实现

由于栈是运算受限的线性表，因此线性表的存储结构对栈也是适用的，只是操作不同而已。

利用顺序存储方式实现的栈称为顺序栈。类似于顺序表的定义，栈中的数据元素用一个预设的足够长度的一维数组elem来实现，栈底位置可以设置在数组的任一个端点，用一个base来作为指向栈底的指针，base为NULL时，表示栈不存在；而栈顶是随着插入和删除而变化的，用一个top 来作为指向栈顶的指针，指明当前栈顶的位置，同样将elem、top和base封装在一个结构中。

顺序栈的类型描述如下：

#define  MAXSIZE  100   

typedef  struct

{  ElemType  elem[MAXSIZE];

   int  base, top;

}SeqStack

定义一个指向顺序栈的指针：SeqStack  *s;

通常将0下标端设为栈底，指针top指向栈顶元素的后一个元素位置。空栈时栈顶指针top=base=0，此时出栈为下溢（underflow); 入栈时，栈顶指针加1，即s->top++; 出栈时，栈顶指针减１，即s->top--。栈操作的示意图如图3.2所示。

图(a)是空栈，图(d)是A、B、C、D、E 、F6个元素依次入栈之后栈满的图示，此时入栈，则上溢（overflow)。通过这个示意图可以要深刻理解栈顶指针的作用。

在上述存储结构上基本操作的实现如下：

（1）置空栈

SeqStack  *Init_SeqStack()

{

SeqStack  *s;

s=malloc(MAXSIZE * sizeof(SeqStack));

s->top=s->base=s;

s->top= 0;  return s;

}

（2）判空栈

    int Empty_SeqStack(SeqStack *s)

      {  

if (s->top= = s->base)  return 1;

        else  return 0;

}

     （3）入栈

int Push (SeqStack *s, elemtype  x)

 { if (s->top= =MAXSIZE)  return 0;      //栈满不能入栈

   else {  

        s->elem[s->top]=x;

s->top++;

        return 1;

}

 }

 （4）出栈

  int Pop (SeqStack *s, elemtype *x)

   {   if  (Empty_SeqStack(s))  return 0;    //栈空不能出栈

       else  {  

s->top--;

*x=s->elem[s->top];        //栈顶元素存入*x，返回

               return 1;

 }       

   }

（5）取栈顶元素

   elemtype Top_SeqStack(SeqStack *s)

   {  

if ( Empty_SeqStack (s) ) return 0;      //栈空

  else return (s->elem[s->top] );

   }

以下几点说明：

   （1）对于顺序栈，入栈时，首先判栈是否满了，栈满的条件为：s->top==MAXSIZE，栈满时，不能入栈；否则出现空间溢出，引起错误，这种现象称为上溢。

   （2）出栈和读栈顶元素操作，先判栈是否为空，为空时不能操作，否则产生错误。通常栈空时常作为一种控制转移的条件。

3.2  栈的应用

由于栈的“先进先出”特点，在很多实际问题中都利用栈做一个辅助的数据结构来进行求解，下面通过几个例子进行说明。

【例3-1】数制转换问题

将十进制数N转换为d进制的数，其转换方法利用辗转相除法：以N=1348，d=8为例转换方法如下：

       N         N / 8 （整除）        N  % 8（求余）

     1348          168                   4                  低

     168           21                    0

     21            2                     5

     2             0                     2                  高

所以：（1348）₁₀  =（2504）₈

可以看出，转换得到的八进制数按低位到高位的顺序产生的，而通常的输出是从高位到低位的，恰好与计算过程相反，因此转换过程中每得到一位8进制数则进栈保存，转换完毕后依次出栈则正好是转换结果。

算法思想如下：当N>0时重复步骤（1）、（2）

（1）若 N≠0，则将N % r 压入栈s中 ，执行步骤（2）；若N=0，将栈s的内容依次出栈，算法结束。

（2）用N / r 代替 N

【例3-2】表达式求值

表达式求值是程序设计语言编译中一个最基本的问题。它的实现是栈应用的一个典型例子。下面介绍一种简单直观、广为使用的表达式求值的算法——算符优先法。

表达式是由操作数、运算符和括号组成的有意义的式子。运算符从操作数的个数上分，有单目运算符和二目运算符；从运算类型上分，有算术运算符、关系运算符和逻辑运算符。在此仅限于讨论只含二目运算符的算术表达式。

（1）中缀表达式求值

中缀表达式：每个二目运算符在两个操作数的中间，假设所讨论的算术运算符包括：+ 、- 、*、/、%、^和（），不难将它推广到更一般的表达式上。

运算符的优先级为：依^ —> ＊、/、% —>+、- —> #次序优先级降低。即^ 的优先级高于 ＊、/、%，而＊、/、%三者优先级相等，即＊、/、%的优先级高于 +、-，而　+、-二者优先级相等，　+、-的优先级高于#，#为表达式起始符和表达式结束符。

规定：同等优先级的，栈顶优先级高，如‘+’号和‘-’号优先级相同，但是如果‘+’号在栈顶，则其优先级高于‘-’；‘(’和‘)’符号优先级相等，‘(’号在栈顶时，小于除了‘)’号的所有符号的优先级，‘)’号在栈顶时，大于除了‘(’号的所有符号的优先级。

中缀表达式的求值过程是：

1）需要两个栈：操作数栈s1和运算符栈s2。首先置操作数栈为空栈，表达式起始符#为运算符栈的栈底元素；

2）当自左至右扫描表达式的每一个字符时，若当前字符是操作数，则入操作数栈，是运算符时，若这个运算符比栈顶运算符优先级高则入栈，继续向后处理，若优先级相等则出栈，继续向后处理，若这个运算符比栈顶运算符优先级低，则从操作数栈出栈两个操作数，从运算符栈出栈一个运算符进行运算，并将其运算结果入操作数栈，继续处理当前字符，直到遇到结束符。

中缀表达式表达式 “#3*2^(4+2*2-1*3)-5#”求值过程中两个栈的状态情况如表3-1所示。

表3-1中缀表达式 #3*2^(4+2*2-1*3)-5# 的求值过程

为了处理方便，编译程序常把中缀表达式首先转换成等价的后缀表达式，后缀表达式的运算符在操作数之后。在后缀表达式中，不再引入括号，所有的计算按运算符出现的顺序，严格从左向右进行，而不用再考虑运算规则和级别。中缀表达式“3+2*(5-1)”的后缀表达式为：“3251-*+”。

（2）后缀表达式求值

计算一个后缀表达式，算法上比计算一个中缀表达式简单的多。这是因为后缀表达式中即无括号又无优先级的约束。

中缀表达式转化为后缀表达式的步骤如下：

1）使用一个栈，先初始化栈，‘#’压栈。

2）当自左至右扫描表达式的每一个字符时，若当前字符是操作数，则输出；若当前字符是运算符时，

a)当前字符大于栈顶字符的优先级时，则压栈，读入下一字符；

b)当前字符等于栈顶字符的优先级时，则栈顶退栈，读入下一字符；

c)当前字符小于栈顶字符的优先级时，则输出栈顶。

3）继续读入字符，遇到结束符‘#’字符时，结束。

后缀表达式的求值过程是：

使用一个栈，当从左向右扫描表达式时，每遇到一个操作数就送入栈中保存，每遇到一个运算符就从栈中取出两个操作数进行当前的计算，然后把结果再入栈，直到整个表达式结束，这时栈顶的值就是结果。

课堂小练习：将中缀表达式“3*2^（4+2*2-1*3）-5”转化为后缀表达式：“32422*+13*-^*5-”，要求写出转化过程，并求值。