对质点的冲量矩等于力矩与力矩作用时间的乘积，即冲量矩ΔL=M·Δt。

对于质点系，由于内力矩可以相互抵消，可得ΔL=(M外+M内)·Δt=(M外+0)·Δt=M外·Δt。

在一段时间内，质点或质点系所受的冲量矩为这段时间内冲量矩的累加，ΔL总=∑ΔL=∑M外·Δt 。（ΔL为矢量，方向与M外相同，单位是N·m·s.）

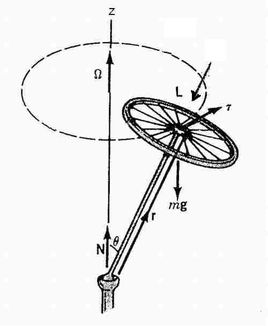
我们知道，质点动量的变化等于外力的冲量，那么质点的角动量如何随外力变化呢？ 

这不难从牛顿运动定律中得到，若质点对某一给点的参考点的角动量 l = r× mv = r×p，则其时间变化率为： 

Δl/Δt=Δ(r×p)/Δt=(Δr/Δt)×p+r×(Δp/Δt) 

若此给定的参考点相对参考系是静止的，则Δr / Δt =v，r × (Δp / Δt) =r × F。 

但力的作用点相对参考点的位矢和力的矢积即为对参考点的力矩M，于是上式又可以写为M =Δl / Δt，即指点对任意定点的角动量的时间变化率等于外力对该点的力矩，这就是质点角动量定理，即： 

Δl=∑M·Δt 

力矩对时间的积累，∑M·Δt就是冲量矩，上式表明，质点角动量的变化量等于外力的冲量矩。