6.2 推断统计与假设检验

当我们对一样本进行测量，得到其平均数、标准误，那么如何判断该样本是否能代表某一总体的水平呢？

•      先作出一个假设：假设这一样本就是来自于相应总体的一个无偏样本。

•      按抽样误差的分布规律来评估其发生概率，如样本测量的平均值与总体平均值相比，差距较大，以至于发生的概率小于0.05，它就成了“小概率事件”，意味着这一推断的前提成立的可能性不大，也是一个小概率事件。

结论：该样本来自于这一总体的可能性很小，它不能代表这一总体，或者说，它与这一总体的差异显著。

 

（1）假设检验概念

假设检验（hypothesistest）又称显著性检验（significance test）,就是根据总体的理论分布和小概率原理，对未知或不完全知道的总体提出两种彼此对立的假设，然后由样本的实际结果，经过一定的计算，判断该样本信息是否支持这种假设，最后在一定概率意义上作出拒绝或不拒绝这种假设的取舍抉择。

 

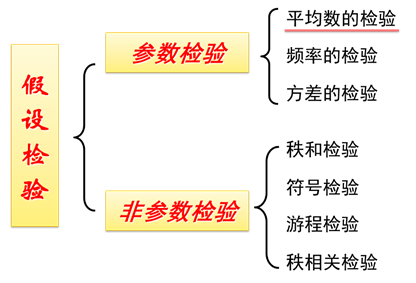
（2）假设检验的步骤

例：通过以往大规模调查，已知某地一般新生儿的头围均数为862.5px。为研究某矿区新生儿的发育状况，现从该地某矿区随机抽取新生儿25人，测得其头围均数为847.25px，标准差为1.99，问该矿区新生儿的头围总体均数与一般新生儿头围总体均数是否不同？

 

1.分析题意，提出假设

抽样误差：该矿区新生儿总体均数与一般新生儿头围总体均数相同

总体差异：该矿区新生儿总体均数与一般新生儿头围总体均数不同

  H₀：μ= μ₀＝34.50    零假设/无效假设

  H_A：μ≠ μ₀＝34.50     备择假设

  考虑样本资料和哪一个假设有较大的矛盾来决定拒绝哪一个假设。一般考察样本资料是否与H₀有较大的矛盾。

 

2.确定显著水平

能否定H₀的人为规定的概率标准称为显著水平，记作a。

统计学中，一般认为概率小于0.05或0.01的事件为小概率事件,所以在小概率原理基础上建立的假设检验也常取a=0.05和a=0.01两个显著水平。

 

3.选定检验方法，计算检验统计量，确定概率值

  根据统计推断目的、实验设计、资料组数、样本含量、等选择方法。如两组小样本（n＜30）比较用t检验、大样本比较u检验、两组及以上样本用方差分析、方差齐性检验用F检验。

 

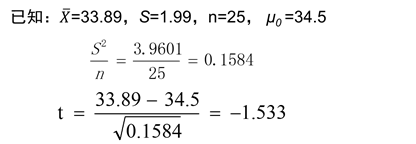
4.作出推断结论：是否接受假设

上例中    P > 0.05   接受H₀

结论：该矿区新生儿的头围总体均数与一般新生儿头围总体均数无显著差异。