6.4 两个样品总体均值的t检验

6.4.1 独立样本T检验

利用来自两个总体的独立样本，推断两个总体的均值是否存在显著差异。

使用前提

（1）独立：两组数据相互独立，互不相关

（2）正态：即两组样本来自的总体符合正态分布

（3）方差齐性：即两组方差相等

 

  例6.3：现希望评价两位老师的教学质量，试比较其分别任教的甲、乙两班（设甲、乙两班原成绩相近，不存在差别）考试后的成绩是否存在差异？见数据“教学例5-3.sav”。

 

SPSS软件中，选择独立样本t检验模块

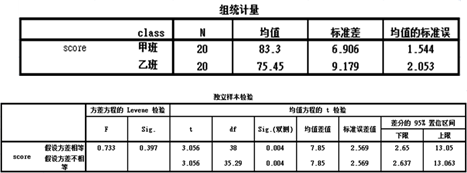
结果显示Levene检验显著性P值为0.397>0.05，故方差齐。不同组间独立样本T检验统计量t=3.056，P值为0.004<0.01，因此认为两位老师分别任教的甲、乙两班考试后的成绩存在极显著差异，即两位老师的教学质量存在极显著差异。

6.4.2 配对样本T检验

  利用来自两个不同总体的配对样本，推断两个总体的均值是否存在显著差异。

配对样本T检验的前提   

 （1）两样本必须是配对的

 （2）样本来自的两个总体应服从正态分布。

 （3）均值是对于检验有意义的描述统计量

 

例6.4：某地区随机抽取12名贫血儿童的家庭，实行健康教育干预三个月，干预前后儿童的血红蛋白（%）测量结果见“血红蛋白例5-4.sav”，试问干预前后该地区贫血儿童血红蛋白（%）平均水平有无变化？

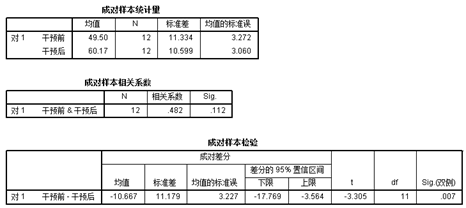
结果显示统计量t=-3.305，P值=0.007<0.01，因此认为干预前后该地区贫血儿童血红蛋白（%）平均水平有变化，结合本案，可以认为该种干预措施可以增加该地区贫血儿童血红蛋白（%）平均水平。