本章概要：理解统计推断的基本方法，掌握单样本t检验、两独立样本t检验和两配对样本t检验的基本思想、适用场合和具体操作。

6.1 推断统计相关概念

ü  总体与样本

   具有相同性质或属性的个体所组成的集合称为总体(population)，它是指研究对象的全体；

从总体中抽出若干个体所构成的集合称为样本(sample)；

研究的目的是要了解总体，然而能观测到的却是样本，通过样本数据来推断总体特征是推断统计分析的基本特点。

•      参数估计

•      假设检验

ü  抽样分布与抽样误差    

样本统计量的概率分布，是一种理论分布。

      在重复选取容量为n的样本时，由该统计量的所有可能取值形成的相对频数分布。

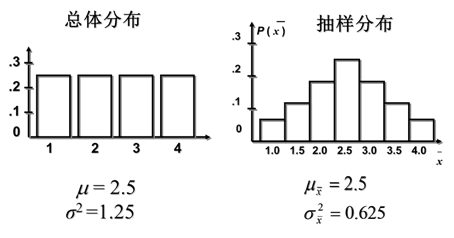
例：设一个总体，含有4个元素(个体)，即总体单位数N=4。4 个个体分别为X₁=1，X₂=2，X₃=3，X₄=4 。总体的均值为2.5、方差1.25。

现从总体中抽取n＝2的简单随机样本，在重复抽样条件下，共有4²=16个样本。

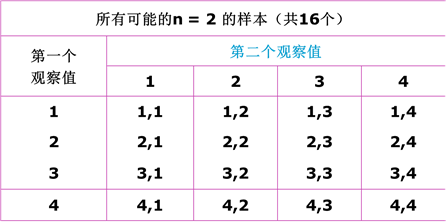
计算出各样本的均值，如下表。并给出样本均值的抽样分布

 

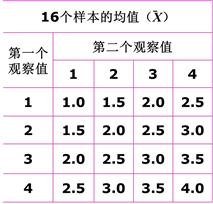
请思考：当我们对一样本进行测量，得到其平均数、标准误，那么如何判断该样本是否能代表某一总体的水平呢？

均数不同，不能说它们来自同一总体

均数相同，不能说它们来自同一总体

 

6.1.2 变量分布的描述

ü  变量的分布    

   有哪些类型？

如何表示变量分布？

 

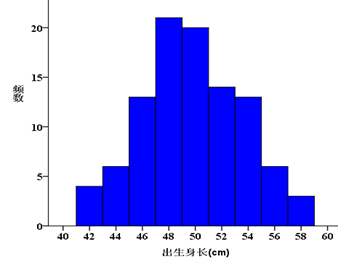
试采用前面所学的方法对下列资料分布进行描述？

 

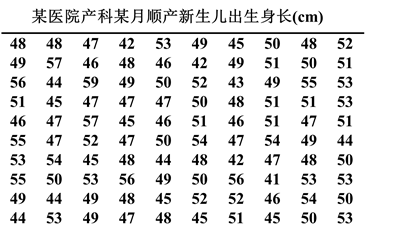
方法：频数分布分析

 

当变量取值范围逐渐增加，到无穷大时，变量分布会是怎样呢？

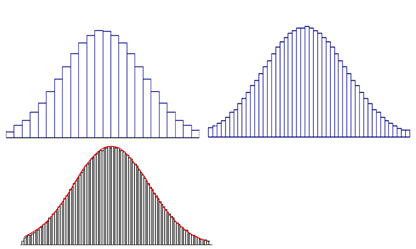
•      随机变量X的概率密度函数。

•      随机变量取一切可能值或范围的概率或概率的规律。

 

6.1.3 正态分布曲线下面积分布规律

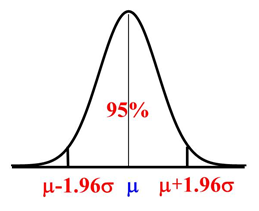
•       X 轴与曲线所夹面积恒等于1或100％。

•       特定区间下面积

•       区间m  ±s的面积为68.27%；

•       区间m  ± 1.96s的面积为95.00%；

•       区间m  ± 2.58s 的面积为99.00%。

 

• 标准正态分布

• 不同变量的正态分布曲线的位置和形状不同（如：身高和体重）；

• 同一变量在不同状态下的正态分布曲线的位置和形状也不同（如：餐前血糖和餐后血糖）；

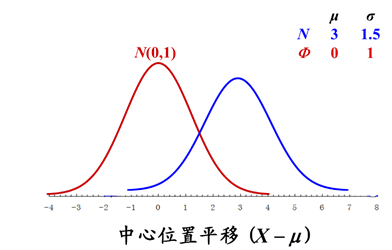
• 通过变量转换可将一般正态分布曲线转化为一条通用的正态分布曲线——标准正态分布曲线。

 

• 一般正态分布向标准正态分布的转换—u变换（也称 Z 变换）

 

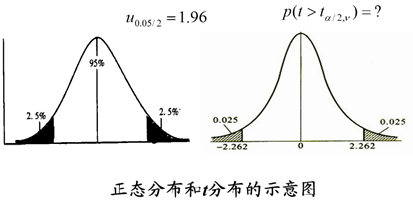
6.1.4 总体参数区间估计—t分布

   当抽样变量值的总体标准差（）未知或抽样样本例数较小时，均数常按t 值转换，抽样均数转换的t_i值组成的分布为t分布（t - distribution）。

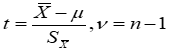
注：统计量t不服从正态分布，服从自由度ν=（n-1)的t分布。

 

（1）t分布的图形与分布特征

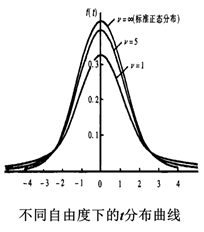
•       以t=0为中心，左右面积对称。

•       t值越大，对应t值外侧面积（概率）越小。

•       t分布型状与自由度(n=n-1 )有关，n越大，t分布曲线形状趋进标准正态分布。

•       每一自由度(n =n-1 )对应一条t分布曲线。

 

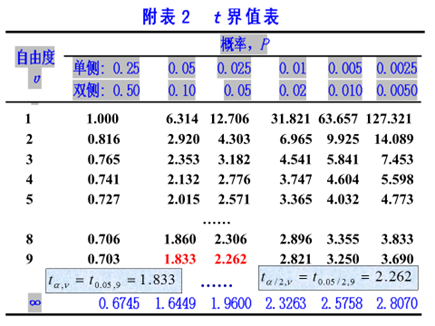
（2）两个分布尾部的界值和概率

 统计中常用分布尾部面积，记为“α”，对应的u值或t值，记为界值，通过与界值比较，对抽样结果进行概率推断。