例题：

　　

　　①先引入三个松弛变量，构造单位矩阵。

　　

　　②得到单位矩阵，构造出初始可行基B

　　

　　从中我们可以get信息：基向量组B和非基向量组N

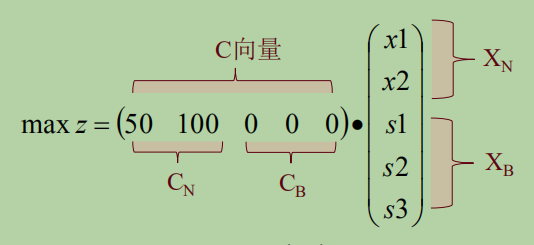
　　还可以知道所有变量的系数所组成的向量C和基变量XB$X_B$、非基变量XN$X_N$：

　　

 　　我们需要的检验数就是系数减去Zj$Z_j$（σj=cj−zj${\sigma }_j=c_j-z_j$，Zj=CBNj$Z_j=C_B{N}_j$）    

　　这是目标函数：Z=CBB−1b+(CN−CBB−1N)XN$Z=C_B{B}^{-1}b+(C_N-C_B{B}^{-1}N)X_N$      (b就是增广矩阵多出来的那些)

　　当基矩阵B化成单位矩阵时，令非基变量XN$X_N$=0，得到 Z=CBB−1b$Z=C_B{B}^{-1}b$ 

 

　　③进行步骤3--6

　　

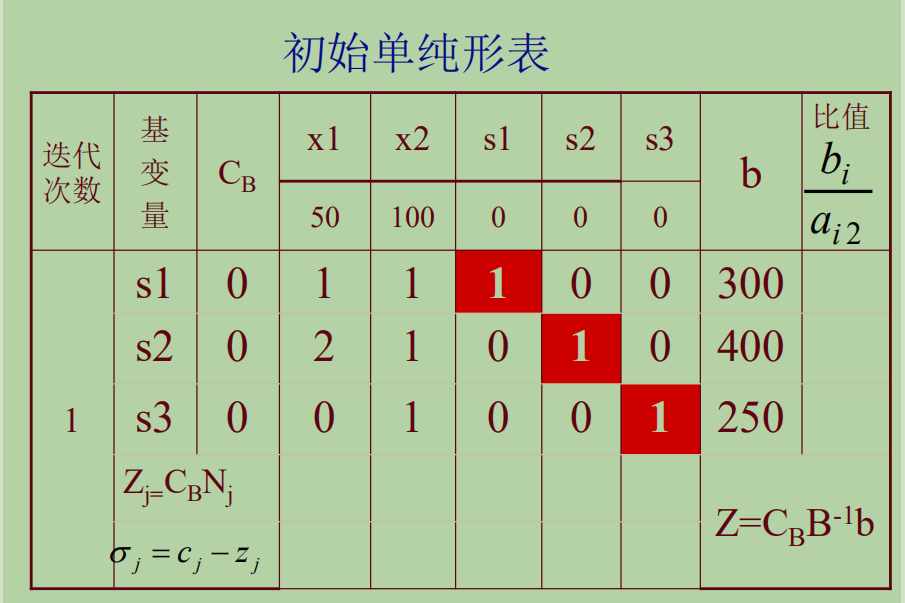
　　填入信息

　　

 

　　刚开始，基变量的系数全为0，所以Z=0，Zj$Z_j$=0，可以写出对应的检验数：

x1	x2	s1	s2	s3
50	100	0	0	0

 

　　可以看出，x2$x_2$对应的检验数最大，成为换入变量，而且根据最小值法则，知道s3$s_3$是换出变量。于是将s3$s_3$的位置换上x2$x_2$，对应的系数也变成了100。

　　

 

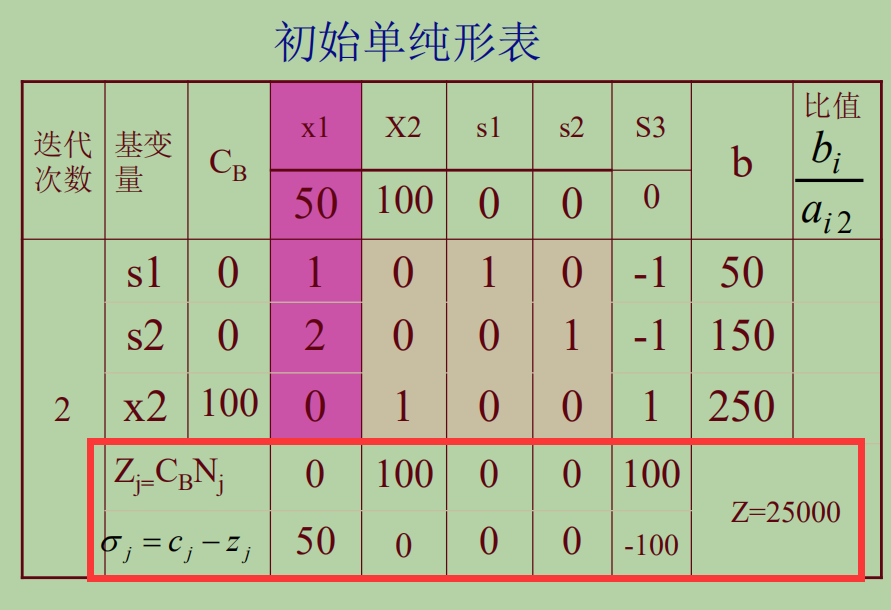
　　我们再进行初等行变换，使x2$x_2$，s1$s_1$，s2$s_2$对应的基矩阵变成单位矩阵。在此基础上进行计算Zj$Z_j$，就可以利用其算出新一轮的检验数：

　　

　　我们可以发现，仍然存在检验数大于0的情况，唉，只能进入新一轮的迭代，x1$x_1$作为换入变量，而经过最小比值规则，可以判定出s1$s_1$是换出变量

　　

　　然后，我们再根据新的数据，写出新一轮的Zj$Z_j$和 检验数 ，发现此时的检验数全部≤0，我们成功地找到了最优解！

　　

　　结束啦！

　　表格中，检验数全部≤0，根据判断规则，Z值为最优值（Z=27500），其解：

　　 X1$X_1$=50，s1$s_1$=50，X2$X_2$=250，s2$s_2$=s3$s_3$=0

　　为模型的最优解。