线性规划的标准型（standard form of linearprogramrmng）线性规划模型的标准形式。其主要特征为：

(1)目标函数为极大化类型；

(2)所有的约束条件都是等式；

(3)所数学规划有约束方程右端的常数都是非负的；

(4)所有决策变量都是非负的。

一、线性规划的一般形式化和特点

线性规划的一般形式形式表示如下：

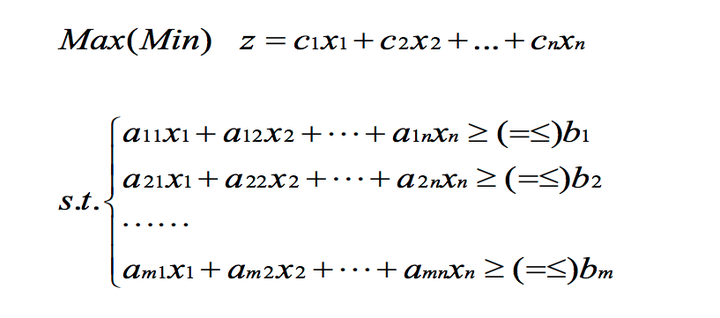
其中相关的知识如下：

因此，我们将约束条件及目标函数都是决策变量的线性函数的规划问题称为线性规划。

二、线性规划的标准型

线性规划的数学模型如下：

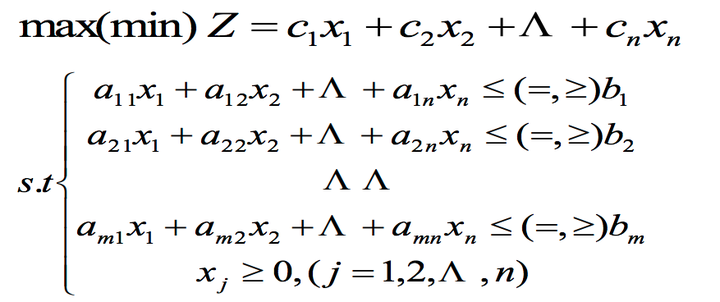
上述模型的简写形式为：

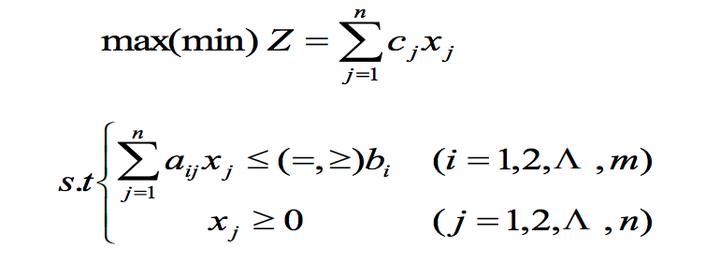
如果用向量表示，可以表示为：

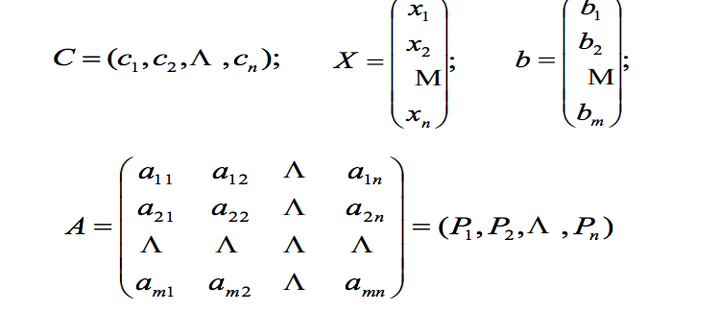
用向量表示时，上述模型可写为：

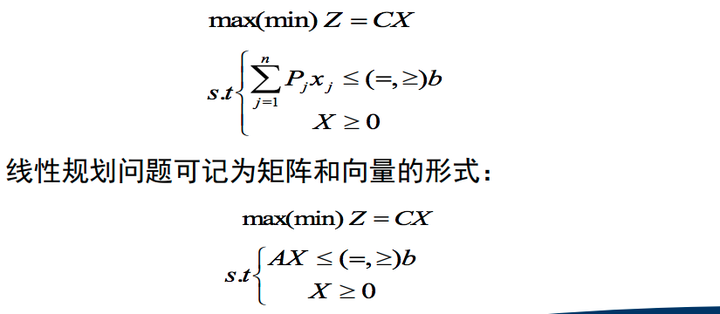
其中线性规划的数学模型的标准形式形式化公式表示如下：

那么线性规划标准型的特征是什么呢？它有下面三个特征

⑴ 求目标函数的最大值（目标函数是求最大值，而不是最小值）；
⑵ 约束条件中变量满足线性方程组与非负性两部分（约束条件中所有x是大于0的）；
⑶ 方程组中右端常数项皆非负（常数项b是非负的）。

三、线性规划的一般形式化标准型方法

我们下面来看一下一般形式如何转换为线性规划标准型的几个例子。

首先看下面这个：

我们可以看到上面的目标函数是求最小值，而不是求最大值，如何转换为标准型，方法如下，就是将目标函数取一个负数转换为求最大值即可。

于是结果变为下面：

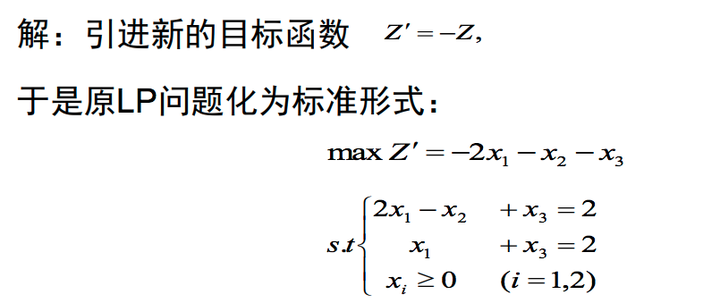
就变成了标准的线性规划问题。

我们在来看下面这个问题：

上面的线性规划问题和标准型相冲突的是约束条件并不是等号（约束方程为不等式）。于是我们可以按照下面的准则：

于是，我们的解法如下：

得到的标准型如下：

我们再来看一个例题：

上述线性规划和我们标准型的区别是，该表达式x3没有约束，约束条件存在不等式，目标函数是求最小值，做法可以按照下面步骤：

于是，我们得到了结果是：

总结

可能有些同学会问线性规划为什么要化成标准形式，用它自身的形式不能够求解吗？

是因为后面对线性规划的求解，在标准型的基础上有一套系统的方法来求解，所以一般是需要化成标准型，并且所有的线性规划通过上述的变型后，都能得到线性规划的标准型。