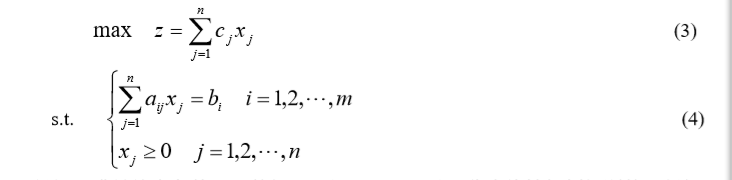1.线性规划的概念
线性规划(Linear Programming 简记 LP)是了运筹学中数学规划的一个重要分支。自从 1947 年 G. B. Dantzig 提出 求解线性规划的单纯形法以来，线性规划在理论上趋向成熟，在实用中由于计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划现代管理中经常采用的基本方法之一。 在解决实际问题时，需要把问题归结成一个线性规划数学模型，关键及难点在于选适当的决策变量建立恰当的模型，这直接影响到问题的求解。
线性规划问题的目标函数及约束条件均为线性函数；约束条件记为 s.t.(即 subject to)。目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以 是小于号也可以是大于号。
一般线性规划问题的（数学）标准型为 ：
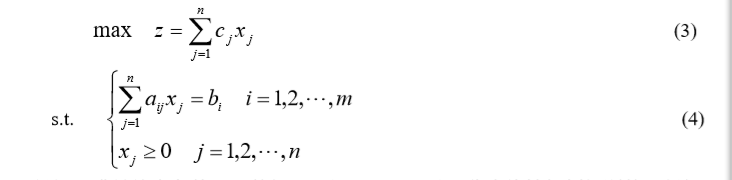
2.线性规划的实例：
3.定义
可行解：满足约束条件的解称为可行解，使目标函数达到最大（小）值的解称为最优解。
基：约束矩阵A为m*n维矩阵，其rank（A）=m（在线性代数中，一个矩阵A的秩是A的线性独立的向量的极大数目，记为rank(A)），设B为A之中的m*m阶非奇异的子矩阵。那么称B为线性规划问题的一个基。（显然rank（B）=m，非奇异意思是： |B| ≠0），
基可行解：由矩阵知识可知，一个基（满秩矩阵）一定会求出一个相应的基解。若一个解既为基解又为可行解，则称为基可行解。可知满足非负条件的基解均为基可行解。
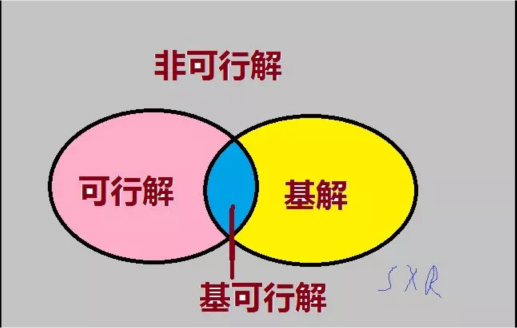图1
4.几何解释
几何看来有时候要领先於分析，但事实上，几何的先行於分析，只不过像一个仆人走在主人的前面一样，是为主人开路的。——西尔维斯特
在使用图解法时，我们理所当然地认为最优解是在可行域的顶点之上，但其中的原因恐怕大部分人没有思考过，更没有去证明过。这一节更像是从几何的角度给出图解法的原理（其实更像是代数的角度），同时得出一些有趣的结论。首先我们需要明确这么几个定义：
凸集（convex set）：设K为n维欧式空间的一个点集，若任意两点的连线上的一点X∈K；则称K为凸集。
凸集的概念很好理解，直观地可以理解为集合没有凹进去的地方，像下图二有凹进去的地方，所以两点的连线之上存在不属于K上的点，故不是凸集。
且凸集的交集仍然为凸集。
另一个注意的地方就是前提必须是在欧氏空间内。（欧氏空间可以不严谨地解释为平坦的空间。）
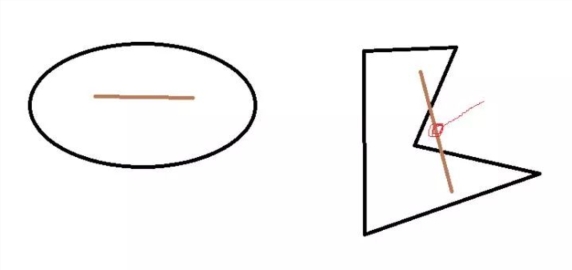图2 一个例子
凸集上无法用不同两点的线性表示的点为顶点。
这两个定义都比较好理解，不做多余解释。有了这些定义与知识，我们可以试着去推出一些定理。
若线性规划存在可行域，则可行域为凸集。
（证明只写思路与关键步骤，有兴趣的读者可以试着写出完整的证明）
引理1：可行解X为基可行解的充要条件为X的正分量对应的系数矩阵非奇异。（系数列向量线性独立）
4.总结
我们介绍了线性规划的概念与标准形式，讨论了加松弛变量将不等式划为标准形式的办法。最后讨论了凸集的性质，得出了几条结论：线性规划的可行解构成的集合为凸集或无界域。基可行解对应凸集的顶点，且线性规划可在凸集的顶点上取到最优解。虽然顶点的个数有限，我们可以用暴力破解法一一求得，再对其进行排序从而找到最优解。但在顶点数目个数较多的时候，这种办法是不太有效的，如何有效地找到最优解，可以进一步学习运筹学之单纯形法。
