FP-growth(Frequent Pattern Tree, 频繁模式树),是韩家炜老师提出的挖掘频繁项集的方法,是将数据集存储在一个特定的称作FP树的结构之后发现频繁项集或频繁项对,即常在一块出现的元素项的集合FP树。
FP-growth算法比Apriori算法效率更高,在整个算法执行过程中,只需遍历数据集2次,就能够完成频繁模式发现,其发现频繁项集的基本过程如下:
(1)构建FP树
(2)从FP树中挖掘频繁项集
FP-growth的一般流程如下:
1:先扫描一遍数据集,得到频繁项为1的项目集,定义最小支持度(项目出现最少次数),删除那些小于最小支持度的项目,然后将原始数据集中的条目按项目集中降序进行排列。
2:第二次扫描,创建项头表(从上往下降序),以及FP树。
3:对于每个项目(可以按照从下往上的顺序)找到其条件模式基(CPB,conditional patten base),递归调用树结构,删除小于最小支持度的项。如果最终呈现单一路径的树结构,则直接列举所有组合;非单一路径的则继续调用树结构,直到形成单一路径即可。
示例说明
如下表所示数据清单(第一列为购买id,第二列为物品项目):
| Tid | Items |
| 1 | I1, I2, I5 |
| 2 | I2, I4 |
| 3 | I2, I3 |
| 4 | I1, I2, I4 |
| 5 | I1, I3 |
| 6 | I2, I3 |
| 7 | I1, I3 |
| 8 | I1, I2, I3, I5 |
| 9 | I1, I2, I3 |
第一步:构建FP树
1. 扫描数据集,对每个物品进行计数:
I1 | I2 | I3 | I4 | I5 |
6 | 7 | 6 | 2 | 2 |
2. 设定最小支持度(即物品最少出现的次数)为2
3. 按降序重新排列物品集(如果出现计数小于2的物品则需删除)
| I2 | I1 | I3 | I4 | I5 |
| 7 | 6 | 6 | 2 | 2 |
4. 根据项目(物品)出现的次数重新调整物品清单
| Tid | Items |
| 1 | I2, I1, I5 |
| 2 | I2, I4 |
| 3 | I2, I3 |
| 4 | I2, I1, I4 |
| 5 | I1, I3 |
| 6 | I2, I3 |
| 7 | I1, I3 |
| 8 | I2, I1, I3, I5 |
| 9 | I2, I1, I3 |
5. 构建FP树
加入第一条清单(I2, I1, I5):
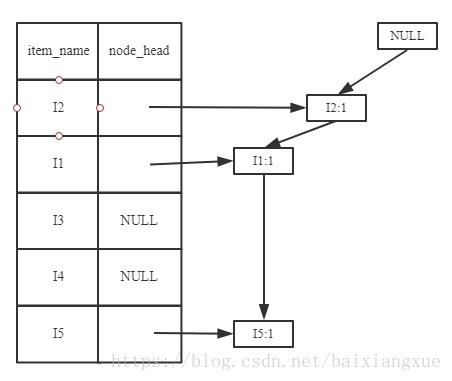
加入第二条清单(I2, I4):
出现相同的节点进行累加(I2)
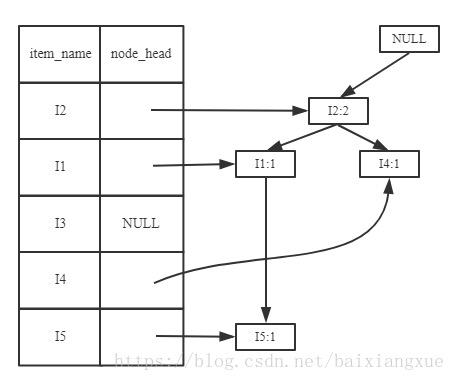
下面依次加入第3-9条清单,得到FP树:
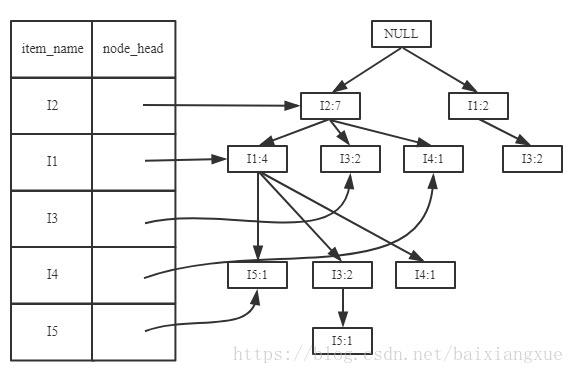
第二步:挖掘频繁项集
对于每一个元素项,获取其对应的条件模式基(conditional pattern base)。条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径。
按照从下往上的顺序,考虑两个例子。
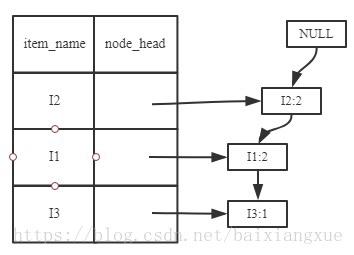
(1)考虑I5,得到条件模式基{(I2 I1:1), (I2 I1 I3)}, 构造条件FP树如下,然后递归调用FP-growth,模式后缀为I5。这个条件FP树是单路径的,在FP-growth中直接列举{I2:2,I1:2,I3:1}的所有组合,之后和模式后缀I5取并集得到支持度大于2的所有模式:{ I2 I5:2, I1 I5:2, I2 I1 I5:2}
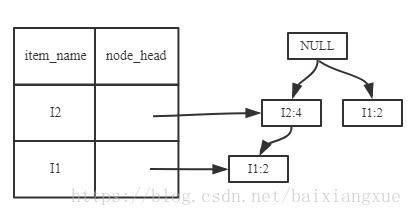
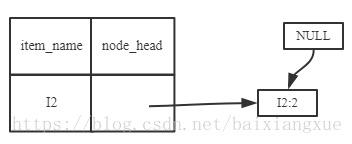
(2)I5的情况是比较简单的,因为I5对应的条件FP-树是单路径的。下面考虑I3,I3的条件模式基是{(I2 I1:2), (I2:2), (I1:2)},生成的条件FP-树如左下图,然后递归调用FP-growth,模式前缀为I3。I3的条件FP-树仍然是一个多路径树,首先把模式后缀I3和条件FP树中的项头表中的每一项取并集,得到一组模式{I2 I3:4, I1 I3:4},但是这一组模式不是后缀为I3的所有模式。还需要递归调用FP-growth,模式后缀为{I1,I3},{I1,I3}的条件模式基为{I2:2},其生成的条件FP-树如右下图所示。这是一个单路径的条件FP-树,在FP-growth中把I2和模式后缀{I1,I3}取并得到模式{I1 I2 I3:2}。理论上还应该计算一下模式后缀为{I2,I3}的模式集,但是{I2,I3}的条件模式基为空,递归调用结束。最终模式后缀I3的支持度大于2的所有模式为:{ I2 I3:4, I1 I3:4, I1 I2 I3:2}
根据FP-growth算法,最终得到的支持度大于2频繁模式如下:
| item | 条件模式基 | 条件FP树 | 产生的频繁模式 |
| I5 | {(I2 I1:1),(I2 I1 I3:1)} | (I2:2, I1:2) | I2 I5:2, I1 I5:2, I2 I1 I5:2 |
| I4 | {(I2 I1:1), (I2:1)} | (I2:2) | I2 I4:2 |
| I3 | {(I2 I1:2), (I2:2), (I1:2)} | (I2:4, I1:2), (I1:2) | I2 I3:4, I1 I3:4, I2 I1 I3:2 |
| I1 | {(I2:4)} | (I2:4) | I2 I1:4 |
FP-growth算法实现
1. FP树的类定义
根据FP-growth算法,最终得到的支持度大于2频繁模式如下:
class treeNode: def __init__(self, nameValue, numOccur, parentNode): self.name = nameValue #节点名字 self.count = numOccur #节点计数值 self.nodeLink = None #用于链接相似的元素项 self.parent = parentNode #needs to be updated self.children = {} #子节点
def inc(self, numOccur): ''' 对count变量增加给定值 ''' self.count += numOccur
def disp(self, ind=1): ''' 将树以文本形式展示 ''' print (' '*ind, self.name, ' ', self.count) for child in self.children.values(): child.disp(ind+1) |
2. FP树构建函数
def createTree(dataSet, minSup=1): ''' 创建FP树 ''' headerTable = {} #第一次扫描数据集 for trans in dataSet:#计算item出现频数 for item in trans: headerTable[item] = headerTable.get(item, 0) + dataSet[trans] headerTable = {k:v for k,v in headerTable.items() if v >= minSup} freqItemSet = set(headerTable.keys()) #print ('freqItemSet: ',freqItemSet) if len(freqItemSet) == 0: return None, None #如果没有元素项满足要求,则退出 for k in headerTable: headerTable[k] = [headerTable[k], None] #初始化headerTable
#print ('headerTable: ',headerTable) #第二次扫描数据集 retTree = treeNode('Null Set', 1, None) #创建树 for tranSet, count in dataSet.items(): localD = {} for item in tranSet: #put transaction items in order if item in freqItemSet: localD[item] = headerTable[item][0]
if len(localD) > 0: orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] updateTree(orderedItems, retTree, headerTable, count)#将排序后的item集合填充的树中
return retTree, headerTable #返回树型结构和头指针表 def updateTree(items, inTree, headerTable, count): if items[0] in inTree.children:#检查第一个元素项是否作为子节点存在 inTree.children[items[0]].inc(count) #存在,更新计数 else: #不存在,创建一个新的treeNode,将其作为一个新的子节点加入其中 inTree.children[items[0]] = treeNode(items[0], count, inTree) if headerTable[items[0]][1] == None: #更新头指针表 headerTable[items[0]][1] = inTree.children[items[0]] else: updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
if len(items) > 1:#不断迭代调用自身,每次调用都会删掉列表中的第一个元素 updateTree(items[1::], inTree.children[items[0]], headerTable, count) def updateHeader(nodeToTest, targetNode): ''' this version does not use recursion Do not use recursion to traverse a linked list! 更新头指针表,确保节点链接指向树中该元素项的每一个实例 '''
while (nodeToTest.nodeLink != None): nodeToTest = nodeToTest.nodeLink nodeToTest.nodeLink = targetNode |
3. 抽取条件模式基
def ascendTree(leafNode, prefixPath): #迭代上溯整棵树 if leafNode.parent != None: prefixPath.append(leafNode.name) ascendTree(leafNode.parent, prefixPath) def findPrefixPath(basePat, treeNode): #treeNode comes from header table condPats = {} while treeNode != None: prefixPath = [] ascendTree(treeNode, prefixPath) if len(prefixPath) > 1: condPats[frozenset(prefixPath[1:])] = treeNode.count treeNode = treeNode.nodeLink
return condPats |
4. 递归查找频繁项集
def mineTree(inTree, headerTable, minSup, preFix, freqItemList): bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1][0])]# 1.排序头指针表 for basePat in bigL: #从头指针表的底端开始 newFreqSet = preFix.copy() newFreqSet.add(basePat) print ('finalFrequent Item: ',newFreqSet) #添加的频繁项列表 freqItemList.append(newFreqSet) condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) print ('condPattBases :',basePat, condPattBases)
# 2.从条件模式基创建条件FP树 myCondTree, myHead = createTree(condPattBases, minSup) # print ('head from conditional tree: ', myHead) if myHead != None: # 3.挖掘条件FP树 print ('conditional tree for: ',newFreqSet) myCondTree.disp(1) mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) |
5. 测试结果
def loadSimpDat(): simpDat=[ ['I1','I2','I5'], ['I2','I4'], ['I2','I3'], ['I1','I2','I4'], ['I1','I3'], ['I2','I3'], ['I1','I3'], ['I1','I2','I3','I5'], ['I1','I2','I3'] ]
return simpDat def createInitSet(dataSet): retDict = {} for trans in dataSet: retDict[frozenset(trans)] = retDict.get(frozenset(trans), 0) + 1 #若没有相同事项,则为1;若有相同事项,则加1 return retDict |
minSup=2 simpDat = loadSimpDat() initSet = createInitSet(simpDat) myFPtree, myHeaderTab = createTree(initSet, minSup) myFPtree.disp() myFreqList = [] mineTree(myFPtree, myHeaderTab, minSup, set([]), myFreqList) |
| myFreqList |


