在数学中经常会看到矩阵，而在程序中常用的是数组，可以简单理解为，矩阵是数学的概念，而数组是计算机程序设计领域的概念。在NumPy中，矩阵是数组的分支，数组和矩阵有些时候是通用的，二维数组也称为矩阵。

一、创建矩阵NumPy

函数库中存在两种不同的数据类型（矩阵matrix和数组array），它们都可以用于处理行列表示的数组元素，虽然它们看起来很相似，但是在这两个数据类型上执行相同的数学运算时，可能得到不同的结果。

在NumPy中，矩阵应用十分广泛。例如，每个图像可以被看作为像素值矩阵。假设一个像素值仅为0和1，那么5×5大小的图像就是一个5×5的矩阵，如图6.25所示，而3×3大小的图像就是一个3×3的矩阵，如图6.26所示。

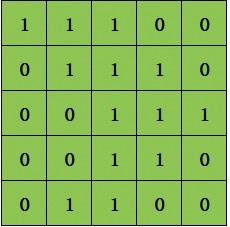
图  5×5矩阵示意图

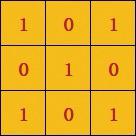
图  3×3矩阵示意图

关于矩阵就简单了解到这里，下面介绍如何在NumPy中创建矩阵。

快速示例43  创建简单的矩阵

使用mat函数创建矩阵，程序代码如下：

01 import numpy as np

02 a = np.mat('5 6;7 8')

03 b = np.mat([[1, 2], [3, 4]])

04 print(a)

05 print(b)

06 print(type(a))

07 print(type(b))

08 n1 = np.array([[1, 2], [3, 4]])

09 print(n1)

10 print(type(n1))

从运行结果得知：mat函数创建的是矩阵类型，array函数创建的是数组类型，而用mat函数创建的矩阵才能进行一些线性代数的操作。

快速示例44  使用mat函数创建常见的矩阵

下面使用mat函数创建常见的矩阵。

（1）创建一个3*3的0（零）矩阵，程序代码如下：

01 import numpy as np

02 #创建一个3*3的零矩阵

03 data1 = np.mat(np.zeros((3,3)))

04 print(data1)

（2）创建一个2*4的1矩阵，程序代码如下：

01 import numpy as np

02 #创建一个2*4的1矩阵

03 data1 = np.mat(np.ones((2,4)))

04 print(data1)

（3）使用random模块的rand函数创建一个3*3在0~1之间随机产生的二维数组，并将其转换为矩阵，程序代码如下：

01 import numpy as np

02 data1 = np.mat(np.random.rand(3,3))

03 print(data1)

（4）创建一个1~8之间的随机整数矩阵，程序代码如下：

01 import numpy as np

02 data1 = np.mat(np.random.randint(1,8,size=(3,5)))

03 print(data1)

（5）创建对角矩阵，程序代码如下：

01 import numpy as np

02 data1 = np.mat(np.eye(2,2,dtype=int)) #2*2对角矩阵

03 print(data1)

04 data1 = np.mat(np.eye(4,4,dtype=int)) #4*4对角矩阵

05 print(data1)

（6）创建对角线矩阵，程序代码如下：

01 import numpy as np

02 a = [1,2,3]

03 data1 = np.mat(np.diag(a))  #对角线1、2、3矩阵

04 print(data1)

05 b = [4,5,6]

06 data1 = np.mat(np.diag(b))  #对角线4、5、6矩阵

07 print(data1)

说明：mat函数只适用于二维矩阵，当维数超过2后，mat就不适用了，从这一点来看array函数更具有通用性。

二、矩阵运算

如果两个矩阵的大小相同，我们可以使用算术运算符“＋”“－”“*”和“/”对矩阵进行加、减、乘、除的运算。

快速示例45  实现矩阵的加法运算

创建两个矩阵data1和data2，实现矩阵的加法运算，效果如图6.27所示。

图  矩阵运算示意图

程序代码如下：

01 import numpy as np

02 #创建矩阵

03 data1= np.mat([[1, 2], [3, 4],[5,6]])

04 data2=np.mat([1,2])

05 print(data1+data2)    #矩阵加法运算

快速示例46  矩阵减法、乘法和除法运算

除了加法运算，还可以实现矩阵的减法、乘法和除法运算。接下来实现矩阵的减法和除法运算，程序代码如下：

01 import numpy as np

02 #创建矩阵

03 data1= np.mat([[1, 2], [3, 4],[5,6]])

04 data2=np.mat([1,2])

05 print(data1-data2)    #矩阵减法运算

06 print(data1/data2)    #矩阵除法运算

当我们对上述矩阵实现乘法运算时，程序出现了错误，原因是矩阵的乘法运算，要求左边矩阵的列和右边矩阵的行数要一致。由于上述矩阵data2是一行，所以导致程序出错。

快速示例47  修改矩阵并进行乘法运算

将矩阵中的data2改为2×2矩阵，再进行矩阵的乘法运算，程序代码如下：

01 import numpy as np

02 #创建矩阵

03 data1= np.mat([[1, 2], [3, 4],[5,6]])

04 data2=np.mat([[1,2],[3,4]])

05 print(data1*data2)    #矩阵乘法运算

上述举例，是两个矩阵直接相乘，称之为矩阵相乘。矩阵相乘是第一个矩阵中与该元素行号相同的元素与第二个矩阵与该元素列号相同的元素，两两相乘后再求和，运算过程如图所示。例如，1×1+2×3=7，是第一个矩阵第1行元素与第二个矩阵第1列元素经过两两相乘求和得到的。

图  矩阵相乘运算过程示意图

数组运算和矩阵运算的一个关键区别是，矩阵相乘使用的是点乘。点乘，也称点积，是数组中元素对应位置一一相乘之后求和的操作，在NumPy中专门提供了点乘方法，即dot方法，该方法返回的是两个数组的点积。

快速示例48  比较数组相乘与数组点乘

比较数组相乘与数组点乘运算，程序代码如下：

01 import numpy as np

02 #创建数组

03 n1 = np.array([1, 2, 3])

04 n2= np.array([[1, 2, 3], [1, 2, 3], [1, 2, 3]])

05 print('数组相乘结果为：','\n',n1*n2)  #数组相乘

06 print('数组点乘结果为：','\n',np.dot(n1, n2))  #数组点乘

快速示例49  实现矩阵元素之间的相乘运算

而要实现矩阵对应元素之间的相乘可以使用multiply函数，程序代码如下：

01 import numpy as np

02 n1 = np.mat('1 3 3;4 5 6;7 12 9') #创建矩阵，使用分号隔开数据

03 n2 = np.mat('2 6 6;8 10 12;14 24 18')

04 print('矩阵相乘结果为：\n',n1*n2)   #矩阵相乘

05 print('矩阵对应元素相乘结果为：\n',np.multiply(n1,n2))

三、矩阵转换

3.1 矩阵转置

快速示例50  使用T属性实现矩阵转置

矩阵转置与数组转置一样需要使用T属性，程序代码如下：

01 import numpy as np

02 n1 = np.mat('1 3 3;4 5 6;7 12 9')  #创建矩阵，使用分号隔开数据

03 print('矩阵转置结果为：\n',n1.T)   #矩阵转置

3.2  矩阵求逆

快速示例51  实现矩阵逆运算

矩阵要可逆，否则意味着该矩阵为奇异矩阵（即矩阵的行列式的值为0）。矩阵求逆主要使用I属性，程序代码如下：

01 import numpy as np

02 n1 = np.mat('1 3 3;4 5 6;7 12 9')  #创建矩阵，使用分号隔开数据

03 print('矩阵的逆矩阵结果为：\n',n1.I)   #逆矩阵

四、NumPy常用统计分析函数

4.1  数学运算函数

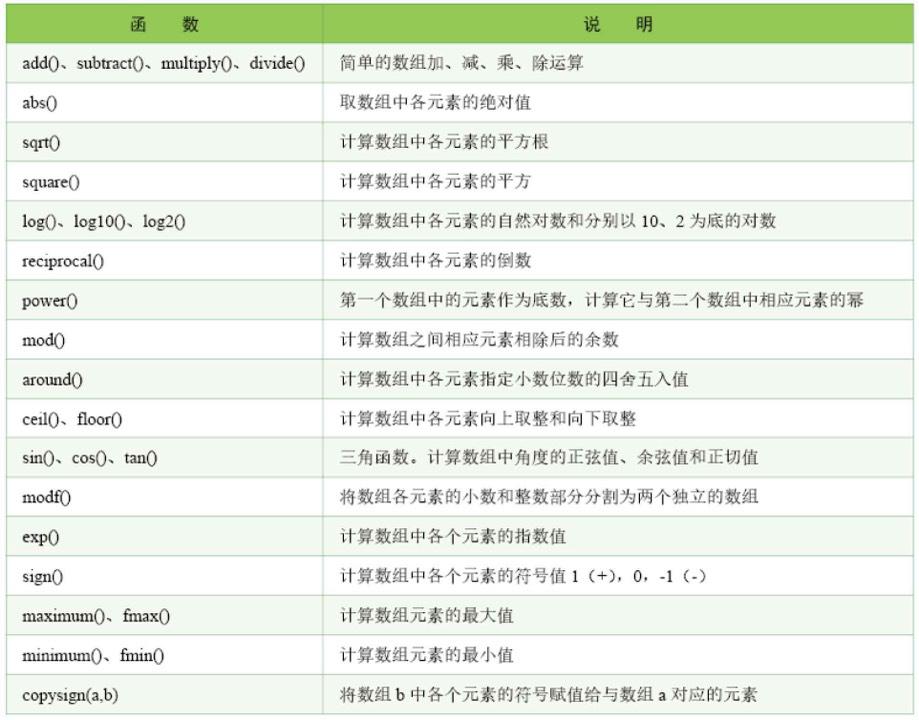
NumPy中包含大量的各种数学运算的函数，包括三角函数、算术运算函数、复数处理函数等，如表所示。

表  数学运算函数及说明

4.1.1  算术函数

（1）加、减、乘、除

NumPy算术函数包含简单的加、减、乘、除，如add函数、subtract函数、multiply函数和divide函数。这里要注意的是数组必须具有相同的形状或符合数组的广播规则。

快速示例52  实现数组加、减、乘、除运算

设置数组加、减、乘、除运算，程序代码如下：

01 import numpy as np

02 n1 = np.array([[1,2,3],[4,5,6],[7,8,9]])  #创建数组

03 n2 = np.array([10, 10, 10])

04 print('两个数组相加：')

05 print(np.add(n1, n2))

06 print('两个数组相减：')

07 print(np.subtract(n1, n2))

08 print('两个数组相乘：')

09 print(np.multiply(n1, n2))

10 print('两个数组相除：')

11 print(np.divide(n1, n2))

（2）倒数

reciprocal函数用于返回数组中各个元素的倒数，如4/3的倒数是3/4。

快速示例53  计算数组元素的倒数

计算数组元素的倒数，程序代码如下：

01 import numpy as np

02 a = np.array([0.25, 1.75, 2, 100])

03 print(np.reciprocal(a))

（3）求幂

power函数将第一个数组中的元素作为底数，计算它与第二个数组中相应元素的幂。

快速示例54  实现数组元素的幂运算

对数组元素进行幂运算，程序代码如下：

01 import numpy as np

02 n1 = np.array([10, 100, 1000])

03 print(np.power(n1, 3))

04 n2= np.array([1, 2, 3])

05 print(np.power(n1, n2))

（4）取余

mod函数用于计算数组之间相应元素相除后的余数。

快速示例55  对数组元素进行取余

对数组元素进行取余，程序代码如下： 

01 import numpy as np

02 n1 = np.array([10, 20, 30])

03 n2 = np.array([4, 5, -8])

04 print(np.mod(n1, n2))

知识胶囊：

下面重点介绍一下Numpy负数取余的算法，公式如下：

r=a-n*[a//n]

其中r为余数，a是被除数，n是除数，“//”为运算取商时保留整数的下界，即偏向于较小的整数。下面针对负数取余的三种不同情况进行举例：

● 余数=30-(-8)*(30//(-8))=30-(-8)*(-4)=30-32=-2

● 余数=-30-(-8)*(-30//(-8))=-30-(-8)*(3)=-30-24=-6

● 余数=-30-(8)*(-30//(8))=-30-(8)*(-4)=-30+32=2

4.1.2  舍入函数

（1）四舍五入around函数

四舍五入在NumPy中应用比较多，主要使用around函数，该函数返回指定小数位数的四舍五入值，语法如下：

numpy.around(a,decimals)

参数说明：■ a：数组。■ decimals：舍入的小数位数，默认值为0，如果为负，整数将四舍五入到小数点左侧的位置。

快速示例56  将数组中的一组数字进行四舍五入

将数组中的一组数字进行四舍五入，程序代码如下：

01 import numpy as np

02 n = np.array([1.55, 6.823,100,0.1189,3.1415926,-2.345]) #创建数组

03 print(np.around(n))   #四舍五入取整

04 print(np.around(n, decimals=2))  #四舍五入保留小数点的后两位

05 print(np.around(n, decimals=-1)) #四舍五入取整到小数点的左侧

（2）向上取整ceil函数

ceil函数用于返回大于或者等于指定表达式的最小整数，即向上取整。

快速示例57  对数组元素进行向上取整

现在对数组元素进行向上取整，程序代码如下：

01 import numpy as np

02 n = np.array([-1.8, 1.66, -0.2, 0.888, 15])  #创建数组

03 print(np.ceil(n))  #向上取整

（3）向下取整floor函数floor函数用于返回小于或者等于指定表达式的最大整数，即向下取整。

快速示例58  对数组元素进行向下取整

对数组元素进行向下取整，程序代码如下：

01 import numpy as np

02 n = np.array([-1.8, 1.66, -0.2, 0.888, 15]) #创建数组

03 print(np.floor(n))  #向下取整

4.1.3  三角函数

NumPy中提供了标准的三角函数：sin函数、cos函数和tan函数。

快速示例59  计算数组的正弦值、余弦值和正切值

计算数组元素的正弦值、余弦值和正切值，程序代码如下：

01 import numpy as np

02 n= np.array([0, 30, 45, 60, 90])

03 print('不同角度的正弦值：')

04 #通过乘pi/180转换为弧度

05 print(np.sin(n * np.pi / 180))

06 print('数组中角度的余弦值：')

07 print(np.cos(n * np.pi / 180))

08 print('数组中角度的正切值：')

09 print(np.tan(n * np.pi / 180))

arcsin函数、arccos函数和arctan函数用于返回给定角度的sin、cos和tan的反三角函数。这些函数的结果可以通过degrees函数将弧度转换为角度。

快速示例60  将弧度转换为角度

首先计算不同角度的正弦值，然后使用arcsin函数计算角度的反正弦，返回值以弧度为单位，最后使用degrees函数将弧度转换为角度来验证结果，程序代码如下：

01 import numpy as np

02 n = np.array([0, 30, 45, 60, 90])

03 print('不同角度的正弦值：')

04 sin = np.sin(n * np.pi / 180)

05 print(sin)

06 print('计算角度的反正弦，返回值以弧度为单位：')

07 inv = np.arcsin(sin)

08 print(inv)

09 print('弧度转换为角度：')

10 print(np.degrees(inv))

4.2  统计分析函数

统计分析函数是指对整个NumPy数组或某条轴的数据进行统计运算，函数介绍如表所示。

表  统计分析函数及说明

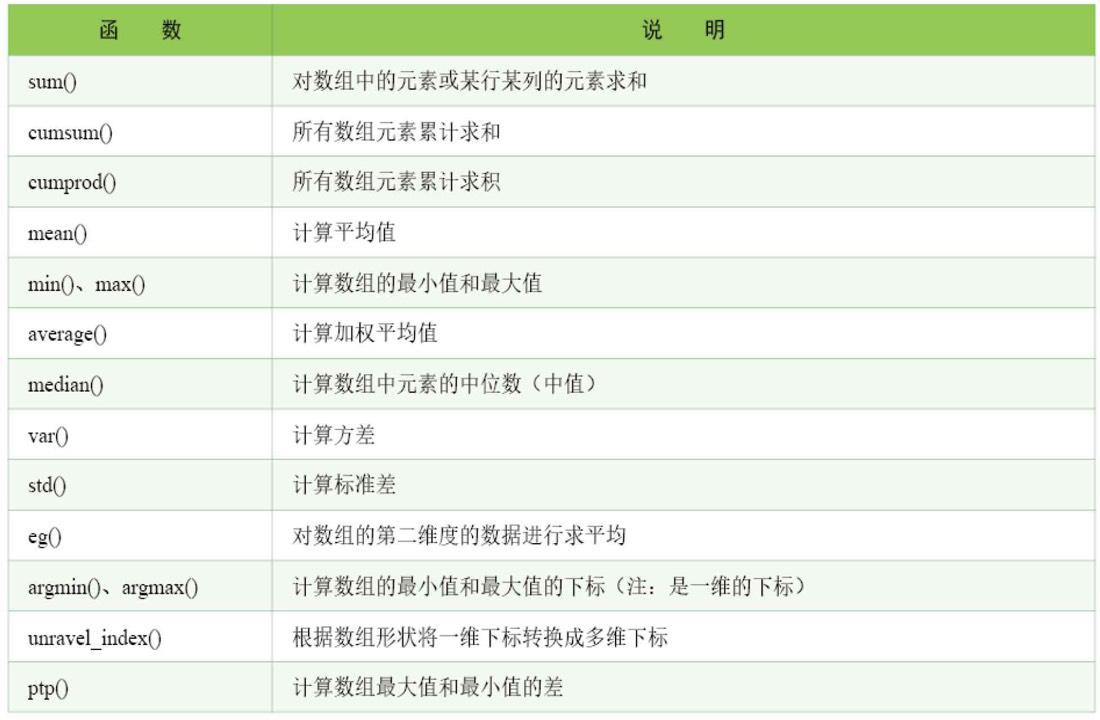
首先创建一个数组，如图所示。

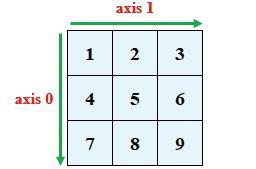
图  数组示意图

4.2.1  求和sum函数

快速示例61  对数组元素及按行列进行求和

对数组元素求和、对数组元素按行和按列求和，程序代码如下：

01 import numpy as np

02 n=np.array([[1,2,3],[4,5,6],[7,8,9]])

03 print('对数组元素求和：')

04 print(n.sum())

05 print('对数组元素按行求和：')

06 print(n.sum(axis=0))

07 print('对数组元素按列求和：')

08 print(n.sum(axis=1))

4.2.2  求平均值mean函数

快速示例62  对数组元素及按行列求平均值

对数组元素求平均值、对数组元素按行求平均值和按列求平均值，关键代码如下：

01 print('对数组元素求平均值：')

02 print(n.mean())

03 print('对数组元素按行求平均值：')

04 print(n.mean(axis=0))

05 print('对数组元素按列求平均值：')

06 print(n.mean(axis=1))

4.2.3  最大值和最小值

快速示例63  对数组元素求最大值和最小值

下面对数组元素求最大值和最小值，关键代码如下：

01 print('数组元素最大值：')

02 print(n.max())

03 print('数组中每一行的最大值：')

04 print(n.max(axis=0))

05 print('数组中每一列的最大值：')

06 print(n.max(axis=1))

07 print('数组元素最小值：')

08 print(n.min())

09 print('数组中每一行的最小值：')

10 print(n.min(axis=0))

11 print('数组中每一列的最小值：')

12 print(n.min(axis=1))

对二维数组求最大值在实际应用中非常广泛。例如，统计销售冠军时就可以使用该方法。

4.2.4  加权平均average函数

在日常生活中，常用平均数表示一组数据的“平均水平”。在一组数据里，一个数据出现的次数称为权。将一组数据与出现的次数相乘再平均计算就是“加权平均”。加权平均能够反映一组数据中的各个数据的重要程度，以及对整体趋势的影响。加权平均在日常生活应用非常广泛，例如考试成绩、股票价格、竞技比赛等。

快速示例64  计算电商各个活动中销售的加权平均价

某电商在开学季、6.18、双十一、双十二等活动的价格都不同，下面计算加权平均价，程序代码如下：

01 import numpy as np

02 price=np.array([34.5,36,37.8,39,39.8,33.6])  #创建“单价”数组

03 number=np.array([900,580,230,150,120,1800])  #创建“销售数量”数组

04 print('加权平均价：')

05 print(np.average(price,weights=number))

4.2.5  中位数median函数

中位数用来衡量数据取值的中等水平或一般水平，可以避免极端值的影响。在数据处理过程中，当数据中存在少量异常值时，它不受其影响，基于这一特点，一般使用中位数来评价分析结果。

那么，什么是中位数？将各个变量值按大小顺序排列起来，形成一个数列，居于数列中间位置的那个数即为中位数。例如，1、2、3、4、5这5个数，中位数就是中间的数字3；而1、2、3、4、5、6这6个数，中位数则是中间两个数即3和4的平均值，即3.5。知识胶囊：

中位数与平均数不同，它不受异常值的影响。例如，将1、2、3、4、5、6改为1、2、3、4、5、288，中位数依然是3.5。

快速示例65  计算电商活动价格的中位数

计算电商在开学季、6.18、双十一、双十二等活动价格的中位数，程序代码如下：

01 import numpy as np

02 n=np.array([34.5,36,37.8,39,39.8,33.6])  #创建“单价”数组

03 # 数组排序后，查找中位数

04 sort_n = np.msort(n)

05 print('数组排序：')

06 print(sort_n)

07 print('数组中位数为：')

08 print(np.median(sort_n))

4.2.6  方差、标准差

快速示例66  求数组的方差和标准差

在NumPy中实现计算数组的方差和标准差，程序代码如下：

01 import numpy as np

02 n=np.array([34.5,36,37.8,39,39.8,33.6])  #创建“单价”数组

03 print('数组方差：')

04 print(np.var(n))

05 print('数组标准差：')

06 print(np.std(n))

4.3  数组的排序

数组的排序即是对数组元素进行排序。

4.3.1  sort函数

使用sort函数进行排序，直接改变原数组，参数axis指定按行排序还是按列排序。

快速示例67  对数组元素按行和列排序

对数组元素按行和列排序，程序代码如下：

01 import numpy as np

02 n=np.array([[4,7,3],[2,8,5],[9,1,6]])

03 print('数组排序：')

04 print(np.sort(n))

05 print('按行排序：')

06 print(np.sort(n,axis=0))

07 print('按列排序：')

08 print(np.sort(n,axis=1))

4.3.2  argsort函数

使用argsort函数对数组进行排序，返回升序排序之后的数组值为从小到大的索引值。

快速示例68  对数组元素升序排序

对数组元素进行升序排序，程序代码如下：

01 import numpy as np

02 x=np.array([4,7,3,2,8,5,1,9,6])

03 print('升序排序后的索引值')

04 y = np.argsort(x)05 print(y)

06 print('排序后的顺序重构原数组')

07 print(x[y])

4.3.3  lexsort函数

lexsort函数用于对多个序列进行排序。可以把它当作是对电子表格进行排序，每一列代表一个序列，排序时会优先照顾靠后的列。

快速示例69  通过排序解决成绩相同学生的录取问题

某重点高中，精英班录取学生按照总成绩录取。由于名额有限，在总成绩相同时，数学成绩高的学生会被优先录取，总成绩和数学成绩都相同时，按照英语成绩高的学生进行优先录取。下面使用lexsort函数对学生成绩进行排序，程序代码如下：

01 import numpy as np

02 math=np.array([101,109,115,108,118,118])      #创建数学成绩

03 en=np.array([117,105,118,108,98,109])         #创建英语成绩

04 total=np.array([621,623,620,620,615,615])     #创建总成绩

05 sort_total=np.lexsort((en,math,total))

06 print('排序后的索引值')

07 print(sort_total)

08 print ('通过排序后的索引获取排序后的数组：')

09 print(np.array([[en[i],math[i],total[i]] for i in sort_total]))

上述举例，按照数学、英语和总成绩进行升序排序，总成绩为620分的2名同学，按照数学成绩高的优先录取原则进行第一轮排序，总成绩为615分的2名同学，同时如果他们的数学成绩也相同，则按照英语成绩高的优先录取原则进行第二轮排序。

五、综合应用

案例1：NumPy实现正态分布

首先简单了解一下什么是正态分布。正态分布，也称为“常态分布”，又名高斯分布，它在数据分析的许多方面有着重大的影响力。正态分布是应用最广泛、常见的一种数据分布的形式。正态分布像一口倒扣的钟表，两头低，中间高，左右对称，大部分数据会集中在平均值，小部分分布在两端。例如，对于学生成绩的分布，高分和低分的成绩一般是少数，分布在两端，而大部分成绩则集中在中间，如图所示。

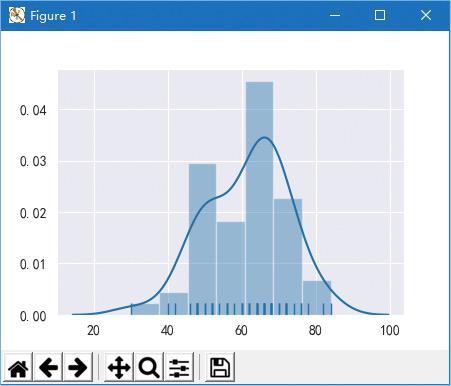
图  学生成绩正态分布示意图

图  正态分布图

下面使用NumPy生成均值为0，标准差为0.1的一维正态分布样本1000个，并用图表显示出来，效果如图6.31所示。程序代码如下：

01 import numpy as np

02 import matplotlib.pyplot as plt

03 import seaborn as sns

04 plt.rcParams['axes.unicode_minus'] = False#用来正常显示负号

05 sns.set_style('darkgrid')

06 n = np.random.normal(0, 0.1, 1000)    #生成均值为0，标准差为0.1的一维正态分布样本1000个

07 print(n)

08 sns.distplot(n)                       #直方图

09 plt.show() #显示

案例2：NumPy用于图像灰度处理

首先了解一下图像，图像其实是由若干像素组成，每一个像素都有明确的位置和被分配的颜色值，因此一张图像也就构成了一个像素矩阵。例如，一张灰度图片的像素块，如图所示。

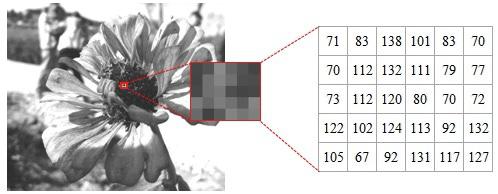
图  灰度图片像素矩阵示意图

从图得知：灰度图片的数据是一个二维数组，颜色取值为0~255。其中，0为黑色，255为白色。从0~255逐渐由暗色变为亮色。由此可见，图像灰度处理是不是就可以通过数组计算来实现呢？

接下来了解一个公式，RGB转换成灰度图像的常用公式：

Gray = R*0.299 + G*0.587 + B*0.114

其中，Gray表示灰度值，R、G、B表示红、绿、蓝颜色值，0.299、0.587、0.114表示灰度公式的固定值。

下面使用NumPy结合Matplotlib实现图像的灰度处理，程序代码如下：

01 import numpy as np

02 import matplotlib.pyplot as plt

03 n1=plt.imread("flower.jpg")    #读取图片

04 plt.imshow(n1)    #传入数组显示对应颜色

05 #n1为三维的数组,最高维是图像的高，次高维是图像的宽，最低维[R,G,B]是颜色值

06 n2=np.array([0.299,0.587,0.114]) #灰度公式的固定值

07 x=np.dot(n1,n2) #将数组n1（RGB颜色值）和数组n2（灰度公式的固定值）中的每个元素进行点乘运算

08 plt.imshow(x,cmap="gray")    #传入数组显示灰度

09 plt.show()   #显示图像

上述代码，在显示灰度图时，需要在imshow中设置参数'cmap="gray"'。

运行程序，对比效果如图所示。

图  原图

图  灰度图像