一、数据探索

根据观测、调查收集到初步的样本数据集后，接下来要考虑的问题是：样本数据集的数量和质量是否满足模型构建的要求？是否出现从未设想过的数据状态？其中有没有什么明显的规律和趋势？各因素之间有什么样的关联性？

通过检验数据集的数据质量、绘制图表、计算某些特征量等手段，对样本数据集的结构和规律进行分析的过程就是数据探索。数据探索有助于选择合适的数据预处理和建模方法，甚至可以完成一些通常由数据挖掘解决的问题。

1.1 数据质量分析

数据质量分析是数据挖掘中数据准备过程的重要一环，是数据预处理的前提，也是数据挖掘分析结论有效性和准确性的基础，没有可信的数据，数据挖掘构建的模型将是空中楼阁。

数据质量分析的主要任务是检查原始数据中是否存在脏数据，脏数据一般是指不符合要求，以及不能直接进行相应分析的数据。在常见的数据挖掘工作中，脏数据包括如下内容。

□　缺失值。

□　异常值。

□　不一致的值。

□　重复数据及含有特殊符号（如#、￥、*）的数据。

1.1.1 缺失值分析

数据的缺失主要包括记录的缺失和记录中某个字段信息的缺失，两者都会造成分析结果的不准确，以下从缺失值产生的原因及影响等方面展开分析。

（1）缺失值产生的原因

有些信息暂时无法获取，或者获取信息的代价太大。

有些信息是被遗漏的。可能是因为输入时认为不重要、忘记填写或对数据理解错误等一些人为因素而遗漏，也可能是由于数据采集设备的故障、存储介质的故障、传输媒体的故障等非人为原因而丢失。

属性值不存在。在某些情况下，缺失值并不意味着数据有错误。对一些对象来说某些属性值是不存在的，如一个未婚者的配偶姓名、一个儿童的固定收入等。

（2）缺失值的影响

数据挖掘建模将丢失大量的有用信息。

数据挖掘模型所表现出的不确定性更加显著，模型中蕴涵的规律更难把握。

包含空值的数据会使建模过程陷入混乱，导致不可靠的输出。

（3）缺失值的分析

使用简单的统计分析，可以得到含有缺失值的属性的个数，以及每个属性的未缺失数、缺失数与缺失率等。

从总体上来说，缺失值的处理分为删除存在缺失值的记录、对可能值进行插补和不处理3种情况。

1.1.2　异常值分析

异常值分析是检验数据是否有录入错误以及含有不合常理的数据。忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会产生不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。

异常值是指样本中的个别值，其数值明显偏离其余的观测值。异常值也称为离群点，异常值的分析也称为离群点分析。

（1）简单统计量分析

可以先对变量做一个描述性统计，进而查看哪些数据是不合理的。最常用的统计量是最大值和最小值，用来判断这个变量的取值是否超出了合理的范围。如客户年龄的最大值为199岁，则该变量的取值存在异常。

（2）3σ原则

如果数据服从正态分布，在3σ原则下，异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。在正态分布的假设下，距离平均值3σ之外的值出现的概率为P（｜x-μ｜>3σ）≤0.003，属于极个别的小概率事件。

如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

（3）箱型图分析

箱型图提供了识别异常值的一个标准：异常值通常被定义为小于QL－1.5IQR或大于QU＋1.5IQR的值。QL称为下四分位数，表示全部观察值中有四分之一的数据取值比它小；QU称为上四分位数，表示全部观察值中有四分之一的数据取值比它大；IQR称为四分位数间距，是上四分位数QU与下四分位数QL之差，其间包含了全部观察值的一半。

箱型图依据实际数据绘制，没有对数据作任何限制性要求（如服从某种特定的分布形式），它只是真实直观地表现数据分布的本来面貌；另一方面，箱型图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的鲁棒性：多达25％的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响。由此可见，箱型图识别异常值的结果比较客观，在识别异常值方面有一定的优越性，如图所示。

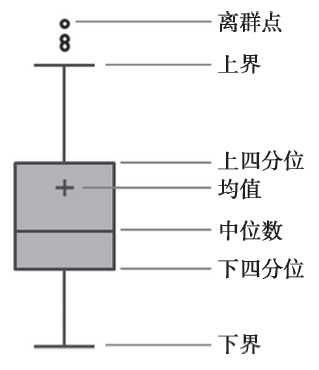
图　箱型图检测异常值

在餐饮系统中的销量额数据可能出现缺失值和异常值，如表中数据所示。

表　餐饮日销额数据示例

分析餐饮系统日销量额数据可以发现，其中有部分数据是缺失的，但是如果数据记录和属性较多，使用人工分辨的方法就不切合实际，所以这里需要编写程序来检测出含有缺失值的记录和属性以及缺失率个数和缺失率等。

在Python的Pandas库中，只需要读入数据，然后使用describe（）函数就可以查看数据的基本情况。

import pandas as pd catering_sale = '../data/catering_sale.xls' #餐饮数据 data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据，指定“日期”列为索引列 data.describe()

运行结果如下：

销量 count　 200.000000 mean　 2755.214700 std　　 751.029772 min　　　22.000000 25％　　2451.975000 50％　　2655.850000 75％　　3026.125000 max　　9106.440000

其中count是非空值数，通过len（data）可以知道数据记录为201条，因此缺失值数为1。另外，提供的基本参数还有平均值（mean）、标准差（std）、最小值（min）、最大值（max）以及1/4、1/2、3/4分位数（25％、50％、75％）。更直观地展示这些数据，并且可以检测异常值的方法是使用箱线图。其Python检测代码如代码清单3-1所示。

代码清单3-1　餐饮销额数据异常值检测代码

import matplotlib.pyplot as plt                        # 导入图像库 plt.rcParams['font.sans-serif'] = ['SimHei']        # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False          # 用来正常显示负号 plt.figure()                                          # 建立图像 p = data.boxplot(return_type='dict')                  # 画箱型图，直接使用DataFrame的方法 x = p['fliers'][0].get_xdata()                          # 'flies'即为异常值的标签 y = p['fliers'][0].get_ydata() y.sort()                                                  # 从小到大排序，该方法直接改变原对象 ''' 用annotate添加注释 其中有些相近的点，注释会出现重叠，难以看清，需要一些技巧来控制 以下参数都是经过调试的，需要具体问题具体调试 ''' for i in range(len(x)):     if i>0:         plt.annotate(y[i], xy=(x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]), y[i]))     else:         plt.annotate(y[i], xy=(x[i],y[i]), xytext=(x[i]+0.08,y[i])) plt.show()                                          # 展示箱型图

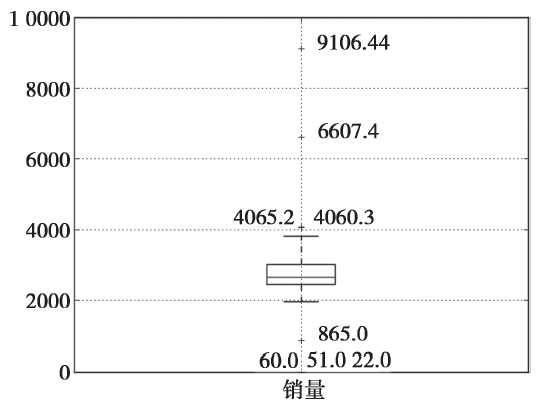
图  异常值检测箱型图

可以看出，箱型图中超过上下界的7个日销售额数据可能为异常值。结合具体业务可以把865.0、4060.3、4065.2归为正常值，将22.0、51.0、60.0、6607.4、9106.44归为异常值。最后确定过滤规则为日销额在400元以下或5000元以上则属于异常数据，编写过滤程序，进行后续处理。

1.1.3　一致性分析

数据不一致性是指数据的矛盾性、不相容性。直接对不一致的数据进行挖掘，可能会产生与实际相违背的挖掘结果。

在数据挖掘过程中，不一致数据的产生主要发生在数据集成的过程中，这可能是由于被挖掘数据是来自于从不同的数据源、对于重复存放的数据未能进行一致性更新造成的。例如，两张表中都存储了用户的电话号码，但在用户的电话号码发生改变时只更新了一张表中的数据，那么这两张表中就有了不一致的数据。

1.2　数据特征分析

对数据进行质量分析以后，接下来可通过绘制图表、计算某些特征量等手段进行数据的特征分析。

1.2.1　分布分析

分布分析能揭示数据的分布特征和分布类型。对于定量数据，欲了解其分布形式是对称的还是非对称的，发现某些特大或特小的可疑值，可通过绘制频率分布表、绘制频率分布直方图、绘制茎叶图进行直观地分析；对于定性分类数据，可用饼图和条形图直观地显示分布情况。

（1）定量数据的分布分析

对于定量变量而言，选择“组数”和“组宽”是做频率分布分析时最主要的问题，一般按照以下步骤进行：

求极差。

决定组距与组数。

决定分点。

列出频率分布表。

绘制频率分布直方图。

遵循的主要原则如下：

各组之间必须是相互排斥的。

各组必须将所有的数据包含在内。

各组的组宽最好相等。

表是描述菜品“捞起生鱼片”在2014年第二个季度的销售数据，通过表中数据绘制销售量的频率分布表、频率分布图，对该定量数据做出相应的分析。

表“捞起生鱼片”的销售情况

求极差

极差＝最大值－最小值＝3960－45＝3915

分组

这里根据业务数据的含义，可取组距为500。

组数＝极差/组距＝3915/500＝7.838

决定分点

分布区间如表所示。

表　分布区间

绘制频率分布直方图

根据分组区间得到如表所示的频率分布表。其中，第1列将数据所在的范围分成若干组段，第1个组段要包括最小值，最后一个组段要包括最大值。习惯上将各组段设为左闭右开的半开区间，如第一个分组为[0，500）。第2列组中值是各组段的代表值，由本组段的上、下限相加除以2得到。第3列和第4列分别为频数和频率。第5列是累计频率，是否需要计算该列视情况而定。

表　频率分布表

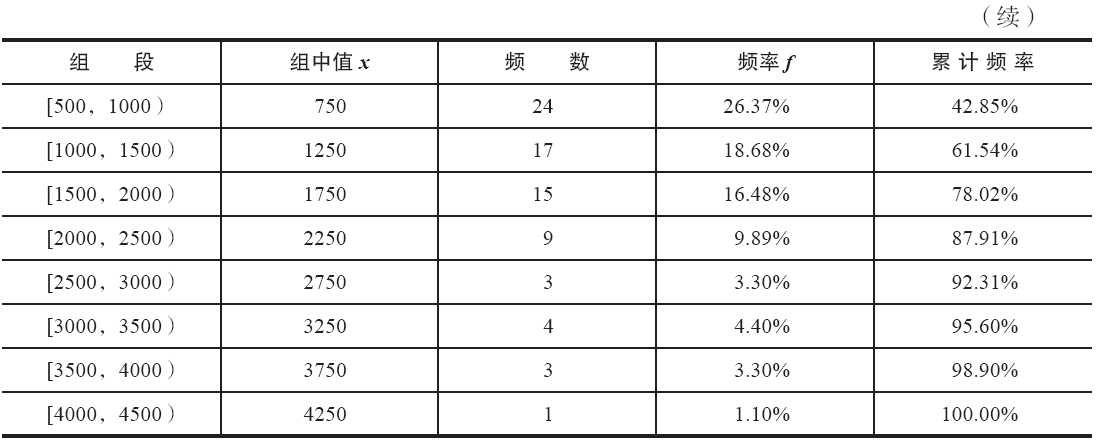
绘制频率分布直方图

若以2014年第二季度“捞起生鱼片”每天的销售额为横轴，以各组段的频率密度（频率与组距之比）为纵轴，表34的数据可绘制成频率分布直方图，如图所示。

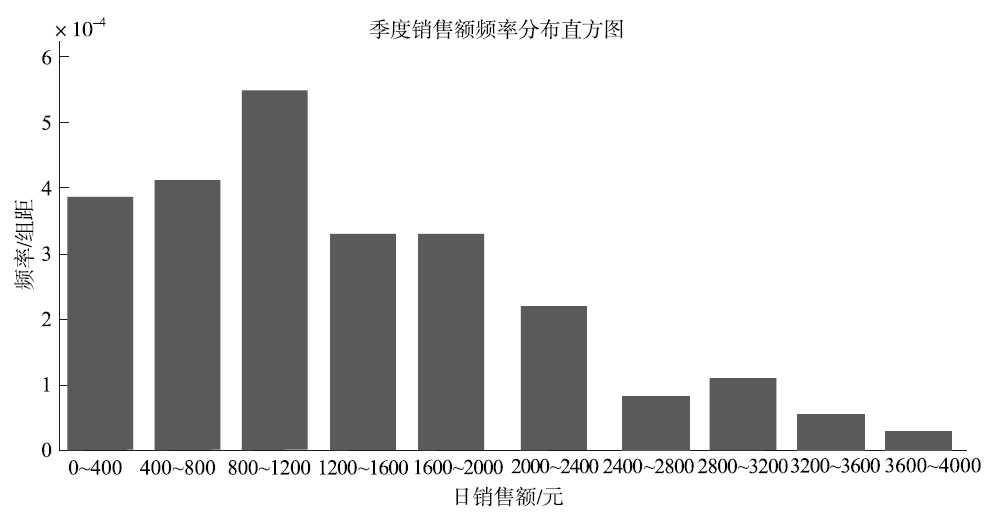
图　销售额的频率分布直方图

（2）定性数据的分布分析

对于定性变量，常常根据变量的分类类型来分组，可以采用饼图和条形图来描述定性变量的分布。

饼图的每一个扇形部分代表每一类型的百分比或频数，根据定性变量的类型数目将饼图分成几个部分，每一部分的大小与每一类型的频数成正比；条形图的高度代表每一类型的百分比或频数，条形图的宽度没有意义。

图是菜品A、B、C在某段时间的销售量的分布图。

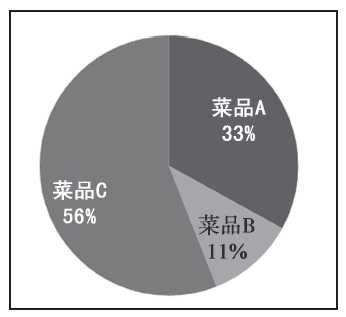
图　菜品销售量分布（饼图）

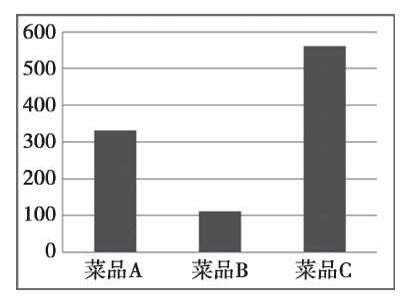
图　菜品的销售量分布（条形图）

1.2.2　对比分析

对比分析是指把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小，水平的高低，速度的快慢，以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中，选择合适的对比标准是十分关键的步骤，只有选择合适，才能做出客观的评价，选择不合适，评价可能得出错误的结论。

对比分析主要有以下两种形式。

（1）绝对数比较

绝对数比较是利用绝对数进行对比，从而寻找差异的一种方法。

（2）相对数比较

相对数比较是由两个有联系的指标对比计算的，用以反映客观现象之间数量联系程度的综合指标，其数值表现为相对数。由于研究目的和对比基础不同，相对数可以分为以下几种。

结构相对数：将同一总体内的部分数值与全部数值对比求得比重，用以说明事物的性质、结构或质量。如居民食品支出额占消费支出总额比重、产品合格率等。

比例相对数：将同一总体内不同部分的数值进行对比，表明总体内各部分的比例关系。如人口性别比例、投资与消费比例等。

比较相对数：将同一时期两个性质相同的指标数值进行对比，说明同类现象在不同空间条件下的数量对比关系。如不同地区商品价格对比，不同行业、不同企业间某项指标对比等。

强度相对数：将两个性质不同但有一定联系的总量指标进行对比，用以说明现象的强度、密度和普遍程度。如人均国内生产总值用“元/人”表示，人口密度用“人/平方公里”表示，也有用百分数或千分数表示的，如人口出生率用壉硎尽？

计划完成程度相对数：是某一时期实际完成数与计划数的对比，用以说明计划完成程度。

动态相对数：将同一现象在不同时期的指标数值进行对比，用以说明发展方向和变化的速度。如发展速度、增长速度等。

就各菜品的销售数据来看，从时间的维度上分析，可以看到甜品部A、海鲜部B、素菜部C三个部门之间的销售金额随时间的变化趋势，可以了解在此期间哪个部门的销售金额较高，趋势比较平稳，如图所示。

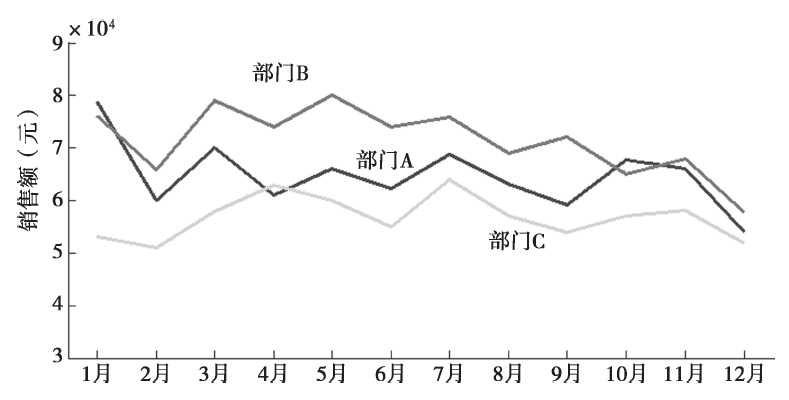
图　部门之间销售金额的比较

从总体来看，三个部门的销售金额呈递减趋势；A部门和C部门的递减趋势比较平稳；B部门的销售金额下降的趋势比较明显，可以进一步分析造成这种现象的原因，可能是原材料不足造成的。

我们也可以对单一部门（如海鲜部）做分析，了解各月份的销售对比情况，如图3-7所示。

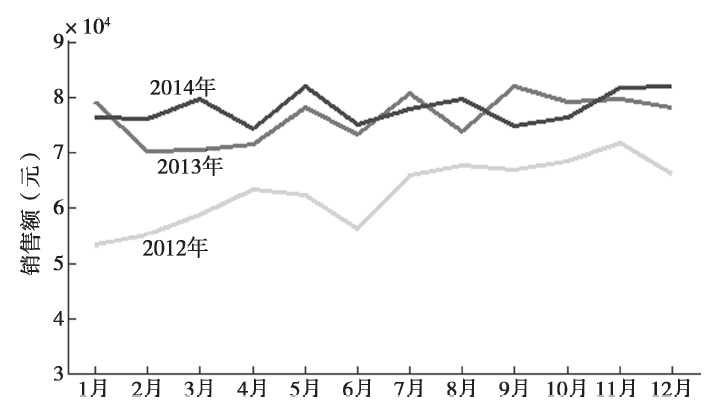
图　海鲜部各年份之间月销售金额的比较

1.2.3　统计量分析

用统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析。

平均水平的指标是对个体集中趋势的度量，使用最广泛的是均值和中位数；反映变异程度的指标则是对个体离开平均水平的度量，使用较广泛的是标准差（方差）、四分位间距。

（1）集中趋势度量

均值

均值是所有数据的平均值。

如果求n个原始观察数据的平均数，计算公式为：

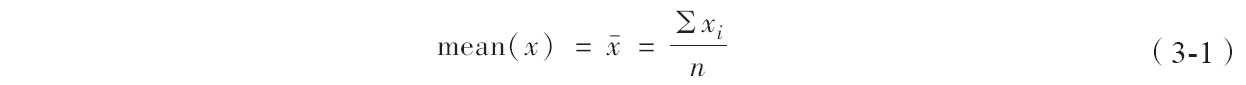
有时，为了反映在均值中不同成分所占的不同重要程度，为数据集中的每一个xi赋予wi，这就得到了加权均值的计算公式：

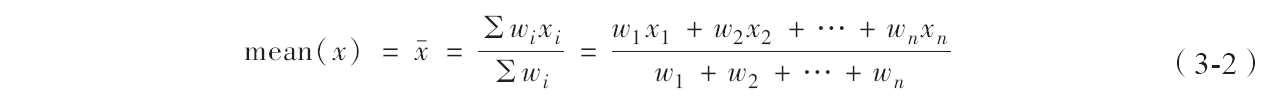
类似地，频率分布表（见表3-4）的平均数可以使用下式计算：

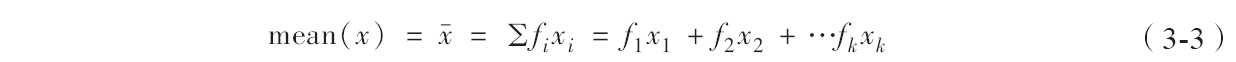
式中，x1，x2，…，xk分别为k个组段的组中值；f1，f2，…，fk分别为k个组段的频率。这里的fi起了权重的作用。

作为一个统计量，均值的主要问题是对极端值很敏感。如果数据中存在极端值或者数据是偏态分布的，那么均值就不能很好地度量数据的集中趋势。为了消除少数极端值的影响，可以使用截断均值或者中位数来度量数据的集中趋势。截断均值是去掉高、低极端值之后的平均数。

中位数

中位数是将一组观察值按从小到大的顺序排列，位于中间的那个数。即在全部数据中，小于和大于中位数的数据个数相等。

将某一数据集x：{x1，x2，…，xn}按从小到大排序：{x（1），x（2），…，x（n）}。

当n为奇数时

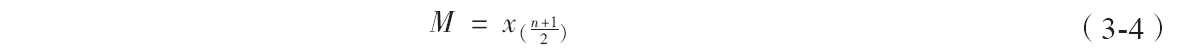
当n为偶数时

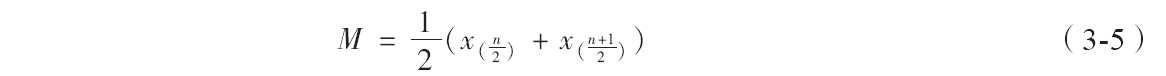
众数

众数是指数据集中出现最频繁的值。众数并不经常用来度量定性变量的中心位置，更适用于定性变量。众数不具有唯一性。当然，众数一般用于离散型变量而非连续型变量。

（2）离中趋势度量

极差

极差＝最大值－最小值

极差对数据集的极端值非常敏感，并且忽略了位于最大值与最小值之间的数据的分布情况。

标准差

标准差度量数据偏离均值的程度，计算公式为：



变异系数

变异系数度量标准差相对于均值的离中趋势，计算公式为：



变异系数主要用来比较两个或多个具有不同单位或不同波动幅度的数据集的离中趋势。

四分位数间距

四分位数包括上四分位数和下四分位数。将所有数值由小到大排列并分成四等份，处于第一个分割点位置的数值是下四分位数，处于第二个分割点位置（中间位置）的数值是中位数，处于第三个分割点位置的数值是上四分位数。

四分位数间距，是上四分位数QU与下四分位数QL之差，其间包含了全部观察值的一半。其值越大，说明数据的变异程度越大；反之，说明变异程度越小。

代码清单3-2　餐饮销量数据统计量分析代码

#-*- coding：utf-8 -*- #餐饮销量数据统计量分析 from __future__ import print_function import pandas as pd catering_sale = '../data/catering_sale.xls' #餐饮数据 data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据，指定“日期”列为索引列 data = data[(data[u'销量'] > 400)&(data[u'销量'] < 5000)] #过滤异常数据 statistics = data.describe() #保存基本统计量 statistics.loc['range'] = statistics.loc['max']-statistics.loc['min'] #极差 statistics.loc['var'] = statistics.loc['std']/statistics.loc['mean'] #变异系数 statistics.loc['dis'] = statistics.loc['75％']-statistics.loc['25％'] #四分位数间距 print(statistics)

运行上面的程序，可以得到下面的结果，此结果为餐饮销量数的统计量情况。

销量 count　 195.000000 mean　 2744.595385 std　　 424.739407 min　　 865.000000 25％　　2460.600000 50％　　2655.900000 75％　　3023.200000 max　　4065.200000 range　3200.200000 var　　　 0.154755 dis　　 562.600000

1.2.4　周期性分析

周期性分析是探索某个变量是否随着时间变化而呈现出某种周期变化趋势。时间尺度相对较长的周期性趋势有年度周期性趋势、季节性周期趋势，相对较短的有月度周期性趋势、周度周期性趋势，甚至更短的天、小时周期性趋势。

例如，要对某单位用电量进行预测，可以先分析该用电单位日用电量的时序图来直观地估计其用电量变化趋势。

图是某用电单位A在2014年9月日用电量的时序图，图3-9是用电单位A在2013年9月日用电量的时序图。

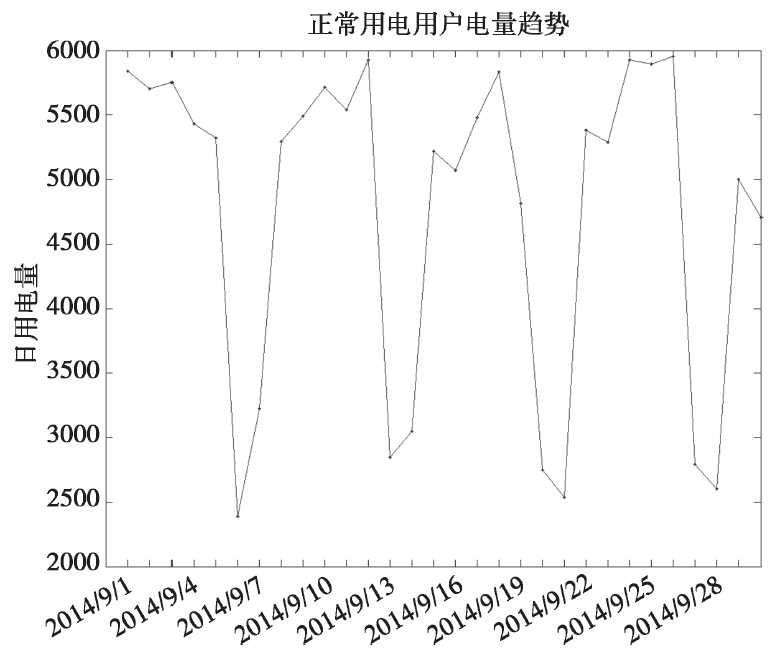
图　2014年9月日用电量时序图

总体来看，用电单位A的2014年9月日用电量呈现出周期性，以周为周期，因为周六周日不上班，所以周末用电量较低。工作日和非工作日的用电量比较平稳，没有太大的波动。而2013年9月日用电量总体呈现出递减的趋势，同样周末的用电量是最低的。

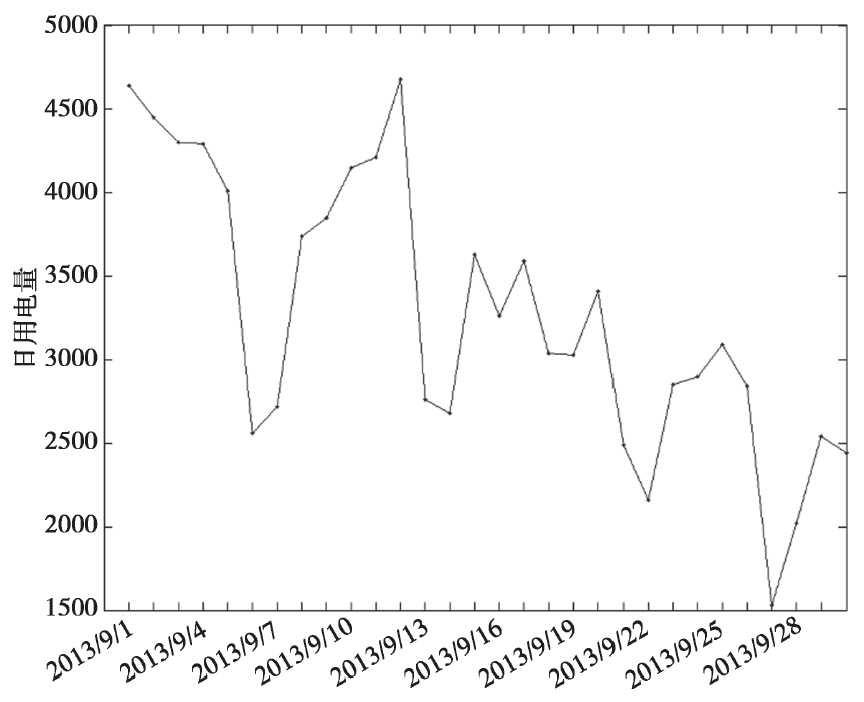
图　2013年9月日用电量时序图

1.2.5　贡献度分析

贡献度分析又称帕累托分析，它的原理是帕累托法则，又称20/80定律。同样的投入放在不同的地方会产生不同的效益。例如，对一个公司来讲，80％的利润常常来自于20％最畅销的产品，而其他80％的产品只产生了20％的利润。

对餐饮企业来讲，应用贡献度分析可以重点改善某菜系盈利最高的前80％的菜品，或者重点发展综合影响最高的80％的部门。这种结果可以通过帕累托图直观地呈现出来。图是海鲜系列的10个菜品A1～A10某个月的盈利额（已按照从大到小排序）。

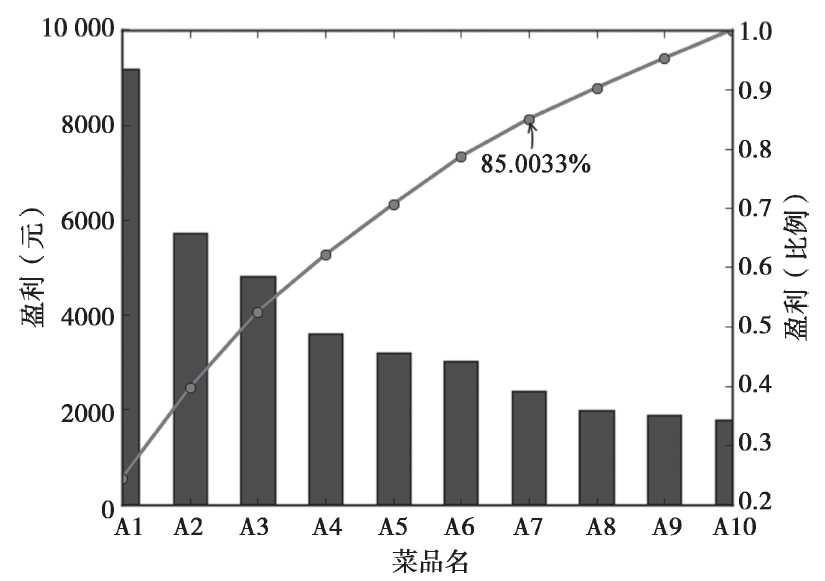
图　帕累托图

由上图可知，菜品A1～A7共7个菜品，占菜品种类数的70％，总盈利额占该月盈利额的85.0033％。根据帕累托法则，应该增加对菜品A1～A7的成本投入，减少对菜品A8～A10的投入以获得更高的盈利额。

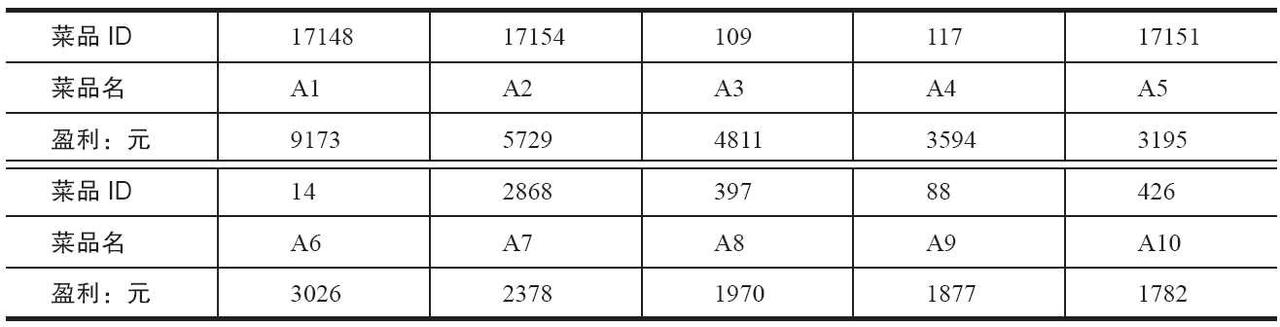
表3-5是餐饮系统对应的菜品盈利数据。

表　餐饮系统菜品盈利数据

其Python代码如代码如下：

代码清单3-3　菜品盈利帕累托图代码

#-*- coding：utf-8 -*- #菜品盈利数据 帕累托图 from __future__ import print_function import pandas as pd #初始化参数 dish_profit = '../data/catering_dish_profit.xls' #餐饮菜品盈利数据 data = pd.read_excel(dish_profit, index_col = u'菜品名') data = data[u'盈利'].copy() data.sort(ascending = False) import matplotlib.pyplot as plt #导入图像库 plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 plt.figure() data.plot(kind='bar') plt.ylabel(u'盈利（元）') p = 1.0*data.cumsum()/data.sum() p.plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2) plt.annotate(format(p[6], '.4％'), xy = (6, p[6]), xytext=(6*0.9, p[6]*0.9), arro 　　wprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) #添加注释，即85％处 　的标记。这里包括了指定箭头样式。 plt.ylabel(u'盈利（比例）') plt.show()

1.2.6　相关性分析

分析连续变量之间线性相关程度的强弱，并用适当的统计指标表示出来的过程称为相关分析。

（1）直接绘制散点图

判断两个变量是否具有线性相关关系的最直观的方法是直接绘制散点图，如图所示。

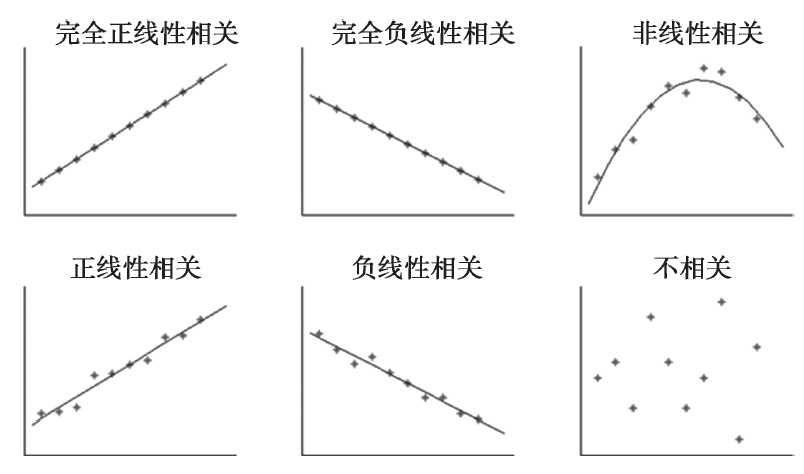
图　相关关系的图示

（2）绘制散点图矩阵

需要同时考察多个变量间的相关关系时，一一绘制它们间的简单散点图是十分麻烦的。此时可利用散点图矩阵同时绘制各变量间的散点图，从而快速发现多个变量间的主要相关性，这在进行多元线性回归时显得尤为重要。

散点图矩阵如图所示。

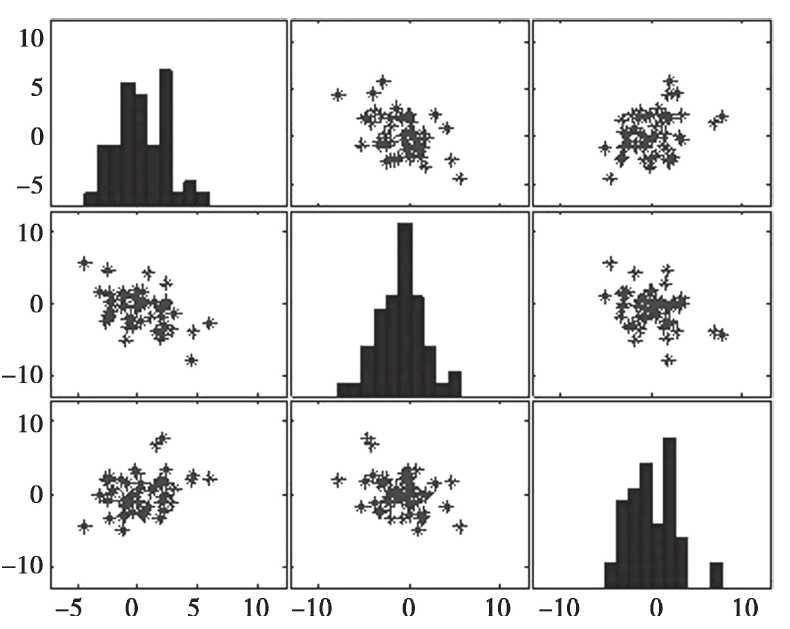
图　散点图矩阵

（3）计算相关系数

为了更加准确地描述变量之间的线性相关程度，可以通过计算相关系数来进行相关分析。在二元变量的相关分析过程中比较常用的有Pearson相关系数、Spearman秩相关系数和判定系数。

Pearson相关系数

一般用于分析两个连续性变量之间的关系，其计算公式如下。

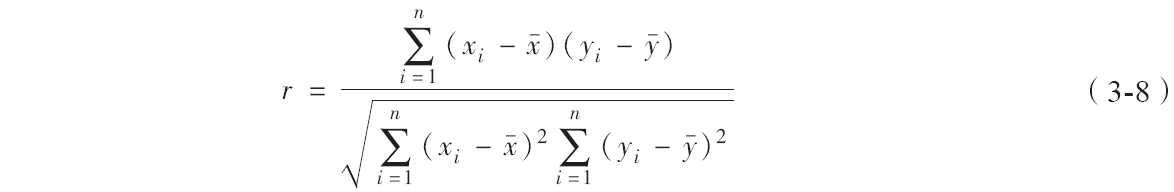
相关系数r的取值范围：-1≤r≤1

0<|r|<1表示存在不同程度线性相关：

Spearman秩相关系数

Pearson线性相关系数要求连续变量的取值服从正态分布。不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数，也称等级相关系数来描述。

其计算公式如下。

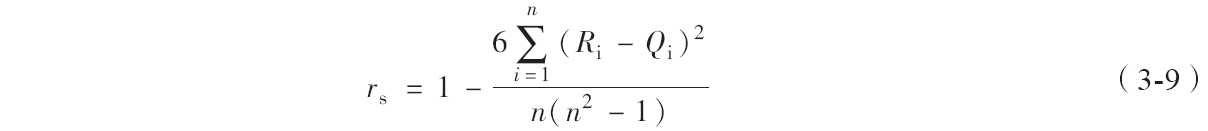
对两个变量成对的取值分别按照从小到大（或者从大到大小）顺序编秩，Ri代表xi的秩次，Qi代表yi的秩次，Ri-Qi为xi、yi的秩次之差。

表给出一个变量x（x1，x2，…xi，…xn）秩次的计算过程。

表　变量x秩次计算过程

因为一个变量的相同的取值必须有相同的秩次，所以在计算中采用的秩次是排序后所在位置的平均值。

只要两个变量具有严格单调的函数关系，那么它们就是完全Spearman相关的，这与Pearson相关不同，Pearson相关只有在变量具有线性关系时才是完全相关的。

在实际应用计算中，上述两种相关系数都要对其进行假设检验，使用t检验方法检验其显著性水平以确定其相关程度。研究表明，在正态分布假定下，Spearman秩相关系数与Pearson相关系数在效率上是等价的，而对于连续测量数据，更适合用Pearson相关系数来进行分析。

（3）判定系数

判定系数是相关系数的平方，用r2表示；用来衡量回归方程对y的解释程度。判定系数取值范围：0≤r2≤1。r2越接近于1，表明x与y之间的相关性越强；r2越接近于0，表明两个变量之间几乎没有直线相关关系。

餐饮系统中可以统计得到不同菜品的日销量数据，数据示例如表所示。

表　菜品日销量数据

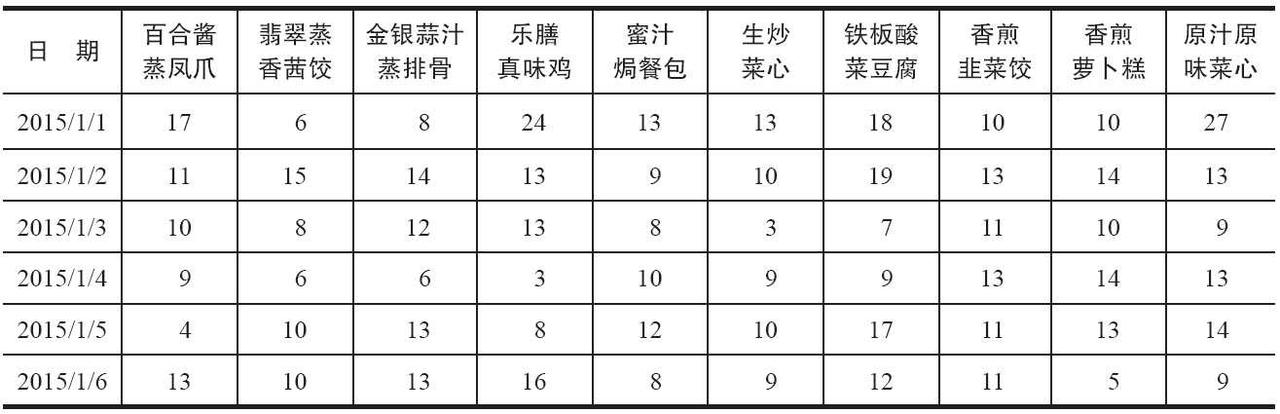
分析这些菜品销售量之间的相关性可以得到不同菜品之间的关系，比如是替补菜品、互补菜品或者没有关系，为原材料采购提供参考。其Python代码如代码清单3-4所示。

代码清单3-4　餐饮销量数据相关性分析

#-*- coding：utf-8 -*- #餐饮销量数据相关性分析 from __future__ import print_function import pandas as pd catering_sale = '../data/catering_sale_all.xls' #餐饮数据，含有其他属性 data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据，指定“日期”列为索引列 data.corr() #相关系数矩阵，即给出了任意两款菜式之间的相关系数 data.corr()[u'百合酱蒸凤爪'] #只显示“百合酱蒸凤爪”与其他菜式的相关系数 data[u'百合酱蒸凤爪'].corr(data[u'翡翠蒸香茜饺']) #计算“百合酱蒸凤爪”与“翡翠蒸香茜饺”的相关系数

上面的代码给出了3种不同形式的求相关系数的运算。运行代码，可以得到任意两款菜式之间的相关系数，如运行“data.corr（）[u'百合酱蒸凤爪']”可以得到下面的结果。

>>> data.corr()[u'百合酱蒸凤爪'] 百合酱蒸凤爪　　 1.000000 翡翠蒸香茜饺　　 0.009206 金银蒜汁蒸排骨　　0.016799 乐膳真味鸡　　　0.455638 蜜汁焗餐包　　　0.098085 生炒菜心　　　 0.308496 铁板酸菜豆腐　　 0.204898 香煎韭菜饺　　　0.127448 香煎萝卜糕　　 -0.090276 原汁原味菜心　　 0.428316 Name：百合酱蒸凤爪, dtype：float64

从上面的结果可以看到，如果顾客点了“百合酱蒸凤爪”，则和点“翡翠蒸香茜饺”“金银蒜汁蒸排骨”“香煎萝卜糕”“铁板酸菜豆腐”“香煎韭菜饺”等主食类的相关性比较低，反而点“乐膳真味鸡”“生炒菜心”“原汁原味菜心”的相关性比较高。

1.3　Python主要数据探索函数

Python中用于数据探索的库主要是Pandas（数据分析）和Matplotlib（数据可视化）。其中，Pandas提供了大量的与数据探索相关的函数，这些数据探索函数可大致分为统计特征函数与统计作图函数，而作图函数依赖于Matplotlib，所以往往又会跟Matplotlib结合在一起使用。本节对Pandas中主要的统计特征函数与统计作图函数进行介绍，并举例以方便理解。

1.3.1　基本统计特征函数

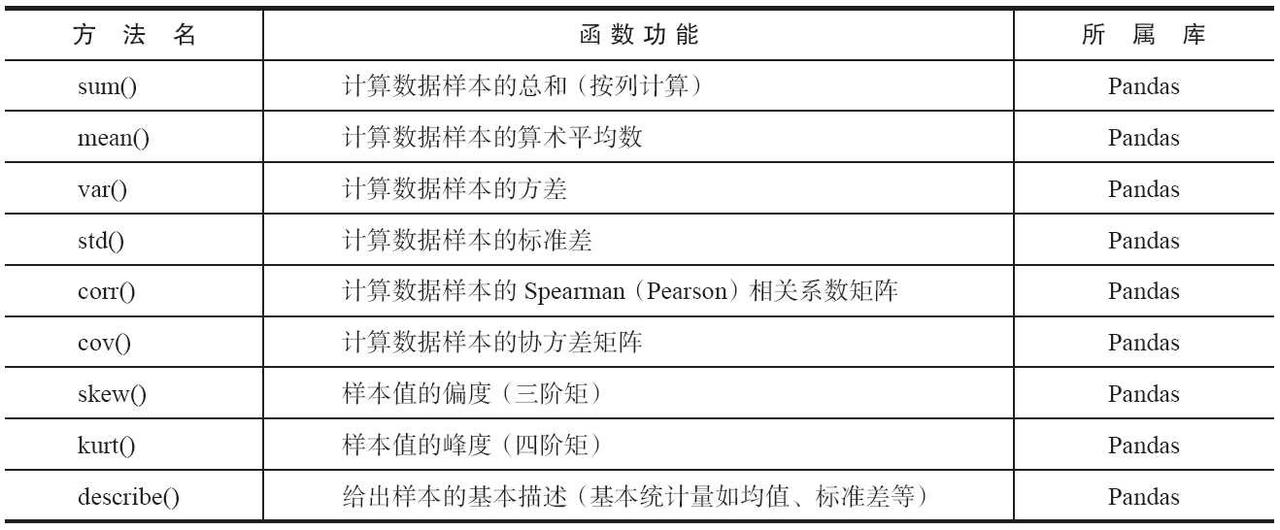
统计特征函数用于计算数据的均值、方差、标准差、分位数、相关系数和协方差等，这些统计特征能反映出数据的整体分布。本小节所介绍的统计特征函数如表3-8所示，它们主要作为Pandas的对象DataFrame或Series的方法出现。

表　Pandas主要统计特征函数

sum

□　功能：计算数据样本的总和（按列计算）。

□　使用格式：D.sum（）

按列计算样本D的总和，样本D可为DataFrame或者Series。

mean

□　功能：计算数据样本的算术平均数。

□　使用格式：D.mean（）

按列计算样本D的均值，样本D可为DataFrame或者Series。

var

□　功能：计算数据样本的方差。

□　使用格式：D.var（）

按列计算样本D的均值，样本D可为DataFrame或者Series。

std

□　功能：计算数据样本的标准差。

□　使用格式：D.std（）

按列计算样本D的均值，样本D可为DataFrame或者Series。

corr

□　功能：计算数据样本的Spearman（Pearson）相关系数矩阵。

□　使用格式：D.corr（method='pearson'）

样本D可为DataFrame，返回相关系数矩阵，method参数为计算方法，支持pearson（皮尔森相关系数，默认选项）、kendall（肯德尔系数）、spearman（斯皮尔曼系数）；

S1.corr（S2，method='pearson'）S1、S2均为Series，这种格式指定计算两个Series之间的相关系数。

□　实例：计算两个列向量的相关系数，采用Spearman方法。

D = pd.DataFrame([range(1, 8), range(2, 9)]) #生成样本D，一行为1～7，一行为2～8 D.corr(method='spearson') #计算相关系数矩阵 S1 = D.loc[0] #提取第一行 S2 = D.loc[1] #提取第二行 S1.corr(S2, method='pearson') #计算S1、S2的相关系数

cov

□　功能：计算数据样本的协方差矩阵。

□　使用格式：D.cov（）

样本D可为DataFrame，返回协方差矩阵；

S1.cov（S2）S1、S2均为Series，这种格式指定计算两个Series之间的协方差。

□　实例：计算6×5随机矩阵的协方差矩阵。

import numpy as np D = pd.DataFrame(np.random.randn(6, 5)) #产生6×5随机矩阵 D.cov() #计算协方差矩阵 D[0].cov(D[1]) #计算第一列和第二列的协方差

结果

0　　　　 1　　　　 2　　　　 3　　　　 4 0　1.745257 -0.299968　0.850216 -0.484931　1.068187 1 -1.453670　1.460928　0.347299　1.585089　0.595347 2 -0.751128　0.504498 -1.244944 -0.672183 -0.595296 3 -0.423802 -1.086470　0.637264　0.873043 -0.506736 4　0.969907　0.721997 -0.550993　1.033300 5 -0.705159　0.385077　0.120580　0.347470　2.036798 0.5

skew/kurt

□　功能：计算数据样本的偏度（三阶矩）/峰度（四阶矩）。

□　使用格式：D.skew（）/D.kurt（）

计算样本D的偏度（三阶矩）/峰度（四阶矩）。样本D可为DataFrame或Series。

□　实例：计算6×5随机矩阵的偏度（三阶矩）/峰度（四阶矩）。

import numpy as np D = pd.DataFrame(np.random.randn(6, 5)) #产生6×5随机矩阵 D.skew() D.kurt()

结果

0　 -0.210246 1　 -0.348367 2　 -1.152183 3　 -0.378802 4　 -0.859889 dtype：float64 0　 -0.191062 1　 -1.831973 2　　1.171797 3　 -1.529854 4　　1.494526 dtype：float64

describe

□　功能：直接给出样本数据的一些基本的统计量，包括均值、标准差、最大值、最小值、分位数等。

□　使用格式：D.describe（）

括号里可以带一些参数，比如percentiles=[0.2，0.4，0.6，0.8]就是指定只计算0.2、0.4、0.6、0.8分位数，而不是默认的1/4、1/2、3/4分位数。

□　实例：给出6×5随机矩阵的describe。

import numpy as np D = pd.DataFrame(np.random.randn(6, 5)) #产生6×5随机矩阵 D.describe()

结果

0　　　　 1　　　　 2　　　　 3　　　　 4 count　6.000000　6.000000　6.000000　6.000000　6.000000 mean　 0.006958 -0.069822　0.113711 -0.168115 -0.584493 std　　1.224979　1.017829　0.939980　1.173083　0.539911 min　 -1.777763 -1.330542 -1.512842 -1.674685 -1.507229 25％　 -0.669088 -0.937504 -0.202329 -1.109370 -0.721853 50％　　0.176010　0.130924　0.472093　0.115791 -0.537366 75％　　0.578993　0.650975　0.516907　0.538483 -0.305514 max　　1.704960　1.119084　1.146215　1.272789　0.086585

1.3.2　拓展统计特征函数

除了上述基本的统计特征外，Pandas还提供了一些非常方便实用的计算统计特征的函数，主要有累积计算（cum）和滚动计算（pd.rolling_），见表。

表　Pandas累积统计特征函数

表　Pandas累积统计特征函数

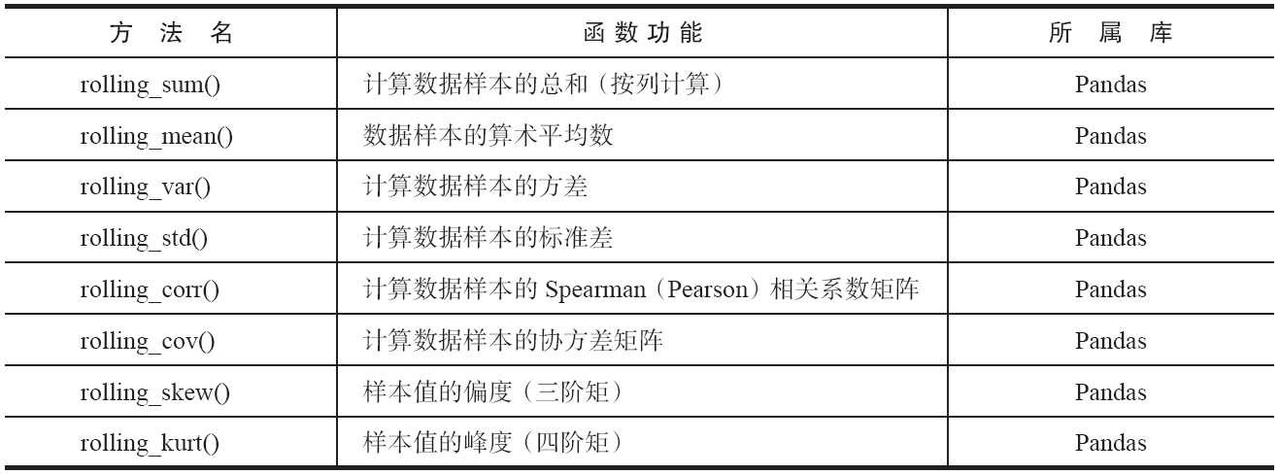
其中，cum系列函数是作为DataFrame或Series对象的方法而出现的，因此命令格式为D.cumsum（），而rolling_系列是pandas的函数，不是DataFrame或Series对象的方法，因此，它们的使用格式为pd.rolling_mean（D，k），意思是每k列计算一次均值，滚动计算。

实例：

D=pd.Series(range(0, 20)) #构造Series，内容为0～19共20个整数 D.cumsum() #给出前n项和 D.rolling(2).sum()#依次对相邻两项求和

结果

0　　　 0 1　　　 1 2　　　 3 3　　　 6…… 19　　190 dtype：int32 0　　NaN 1　　　1 2　　　3 3　　　5…… 19　　37 dtype：float64

1.3.3　统计作图函数

通过统计作图函数绘制的图表可以直观地反映出数据及统计量的性质及其内在规律，如盒图可以表示多个样本的均值，误差条形图能同时显示下限误差和上限误差，最小二乘拟合曲线图能分析两变量间的关系。

Python的主要作图库是Matplotlib，在第2章中已经进行了初步的介绍，而Pandas基于Matplotlib并对某些命令进行了简化，因此作图通常是Matplotlib和Pandas相互结合着使用。本小节仅对一些基本的作图函数做一下简介，而真正灵活地使用应当参考书中所给出的各个作图代码清单。我们要介绍的统计作图函数如表所示。

表　Python主要统计作图函数

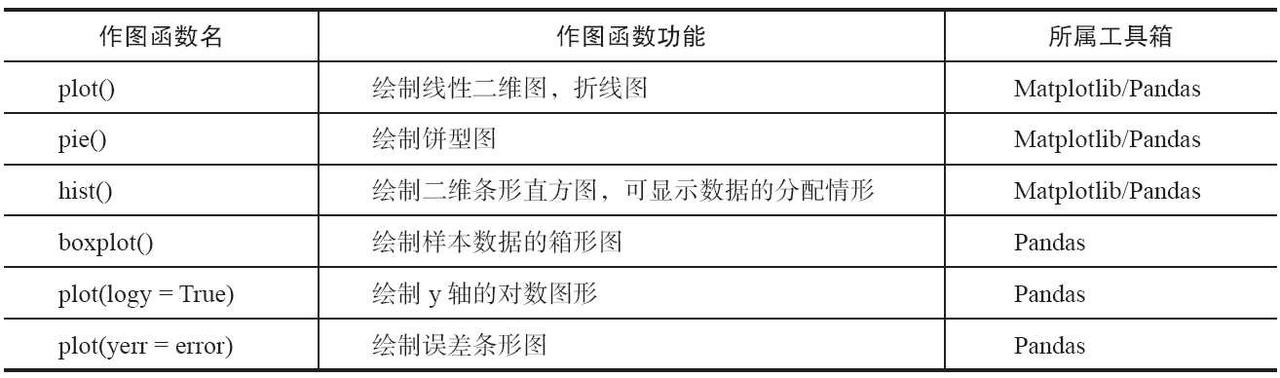
在作图之前，通常要加载以下代码。

import matplotlib.pyplot as plt #导入作图库 plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 plt.figure(figsize = (7, 5)) #创建图像区域，指定比例

作图完成后，一般通过plt.show（）来显示作图结果。

（1）plot

□　功能：绘制线性二维图、折线图。

□　使用格式：plt.plot（x，y，S）

这是Matplotlib通用的绘图方式，绘制y对于x（即以x为横轴的二维图形），字符串参量S指定绘制时图形的类型、样式和颜色，常用的选项有：'b'为蓝色、'r'为红色、'g'为绿色、'o'为圆圈、'+'为加号标记、'-'为实线、'——'为虚线。当x、y均为实数同维向量时，则描出点（x（i），y（i）），然后用直线依次相连。

D.plot（kind='box'）

这里使用的是DataFrame或Series对象内置的方法作图，默认以Index为横坐标，每列数据为纵坐标自动作图，通过kind参数指定作图类型，支持line（线）、bar（条形）、barh、hist（直方图）、box（箱线图）、kde（密度图）和area、pie（饼图）等，同时也能够接受plt.plot（）中接受的参数。因此，如果数据已经被加载为Pandas中的对象，那么以这种方式作图是比较简洁的。

□　实例：在区间（0≤x≤2π）绘制一条蓝色的正弦虚线，并在每个坐标点标上五角星。绘制图形如图所示。

import numpy as np x = np.linspace(0,2*np.pi,50) #x坐标输入 y = np.sin(x) #计算对应x的正弦值 plt.plot(x, y, 'bp——') #控制图形格式为蓝色带星虚线，显示正弦曲线 plt.show()

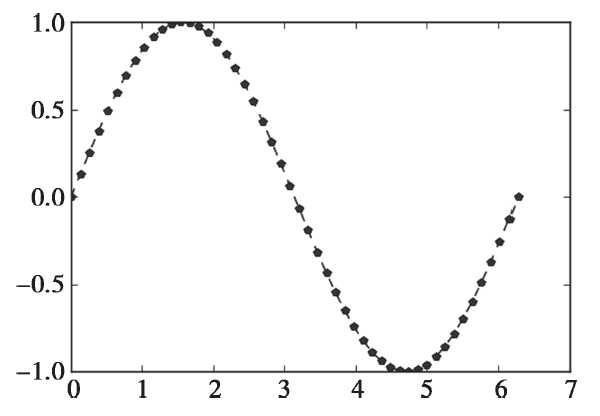
图　正弦曲线图

（2）pie

□　功能：绘制饼型图。

□　使用格式：plt.pie（size）

使用Matplotlib绘制饼图，其中size是一个列表，记录各个扇形的比例。pie有丰富的参数，详情请参考下面的实例。

□　实例：通过向量[15，30，45，10]画饼图，注上标签，并将第2部分分离出来。绘制结果如图所示。

import matplotlib.pyplot as plt # The slices will be ordered and plotted counter-clockwise. labels = 'Frogs', 'Hogs', 'Dogs', 'Logs' #定义标签 sizes = [15, 30, 45, 10] #每一块的比例 colors = ['yellowgreen', 'gold', 'lightskyblue', 'lightcoral'] #每一块的颜色 explode = (0, 0.1, 0, 0) #突出显示，这里仅仅突出显示第二块（即'Hogs'） plt.pie(sizes, explode=explode, labels=labels, colors=colors, autopct='％1.1f％％',  　　shadow=True, startangle=90) plt.axis('equal') #显示为圆（避免比例压缩为椭圆） plt.show()

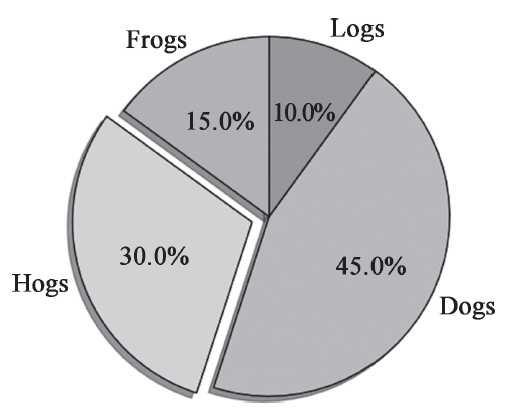
图　饼形图

（3）hist

□　功能：绘制二维条形直方图，可显示数据的分布情形。

□　使用格式：Plt.hist（x，y）

其中，x是待绘制直方图的一维数组，y可以是整数，表示均匀分为n组；也可以是列表，列表各个数字为分组的边界点（即手动指定分界点）。

□　实例：绘制二维条形直方图，随机生成有1000个元素的服从正态分布的数组，分成10组绘制直方图。绘制结果如图所示。

import matplotlib.pyplot as plt import numpy as np x = np.random.randn(1000) #1000个服从正态分布的随机数 plt.hist(x, 10) #分成10组进行绘制直方图 plt.show()

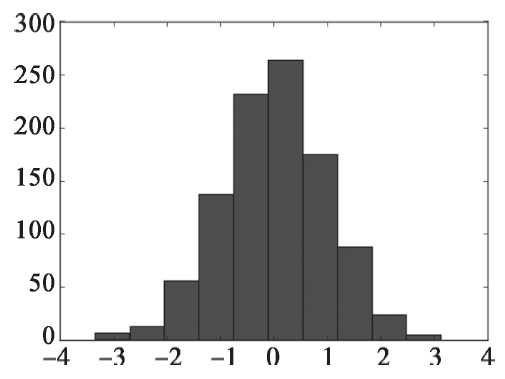
图　二维条形直方图

（4）boxplot

□　功能：绘制样本数据的箱形图。

□　使用格式：D.boxplot（）/D.plot（kind='box'）

有两种比较简单的方式绘制D的箱形图，其中一种是直接调用DataFrame的boxplot（）方法；另外一种是调用Series或者DataFrame的plot（）方法，并用kind参数指定箱形图（box）。其中，盒子的上、下四分位数和中值处有一条线段。箱形末端延伸出去的直线称为须，表示盒外数据的长度。如果在须外没有数据，则在须的底部有一点，点的颜色与须的颜色相同。

□　实例：绘制样本数据的箱形图，样本由两组正态分布的随机数据组成。其中，一组数据均值为0，标准差为1，另一组数据均值为1，标准差为1。绘制结果如图所示。

import matplotlib.pyplot as plt import numpy as np import pandas as pd x = np.random.randn(1000) #1000个服从正态分布的随机数 D = pd.DataFrame([x, x+1]).T #构造两列的DataFrame D.plot(kind = 'box') #调用Series内置的作图方法画图，用kind参数指定箱形图box plt.show()

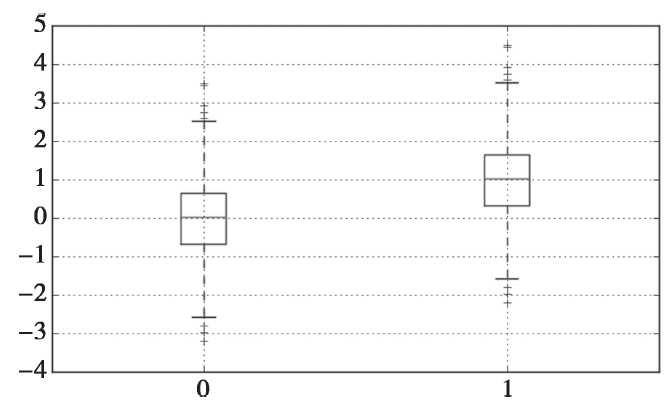
图　箱形图

（5）plot（logx=True）/plot（logy=True）

□　功能：绘制x或y轴的对数图形。

□　使用格式：D.plot（logx=True）/D.plot（logy=True）

对x轴（y轴）使用对数刻度（以10为底），y轴（x轴）使用线性刻度，进行plot函数绘图，D为Pandas的DataFrame或者Series。

□　实例：构造指数函数数据使用plot（logy=True）函数进行绘图，绘制结果如图所示。

import matplotlib.pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 import numpy as np import pandas as pd x = pd.Series(np.exp(np.arange(20))) #原始数据 x.plot(label = u'原始数据图', legend = True) plt.show() x.plot(logy = True, label = u'对数数据图', legend = True) plt.show()

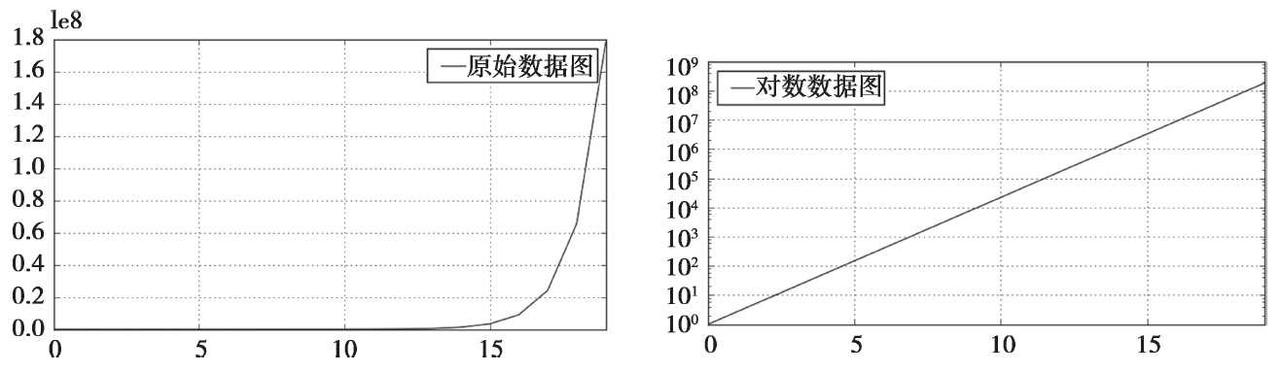
图　y轴的对数图形对比图

（6）plot（yerr=error）

□　功能：绘制误差条形图。

□　使用格式：D.plot（yerr=error）

绘制误差条形图。D为Pandas的DataFrame或Series，代表着均值数据列，而error则是误差列，此命令在y轴方向画出误差棒图；类似地，如果设置参数xerr=error，则在x轴方向画出误差棒图。

□　实例：绘制误差棒图。绘制结果如图所示。

import matplotlib.pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 import numpy as np import pandas as pd error = np.random.randn(10) #定义误差列 y = pd.Series(np.sin(np.arange(10))) #均值数据列 y.plot(yerr = error) #绘制误差图 plt.show()

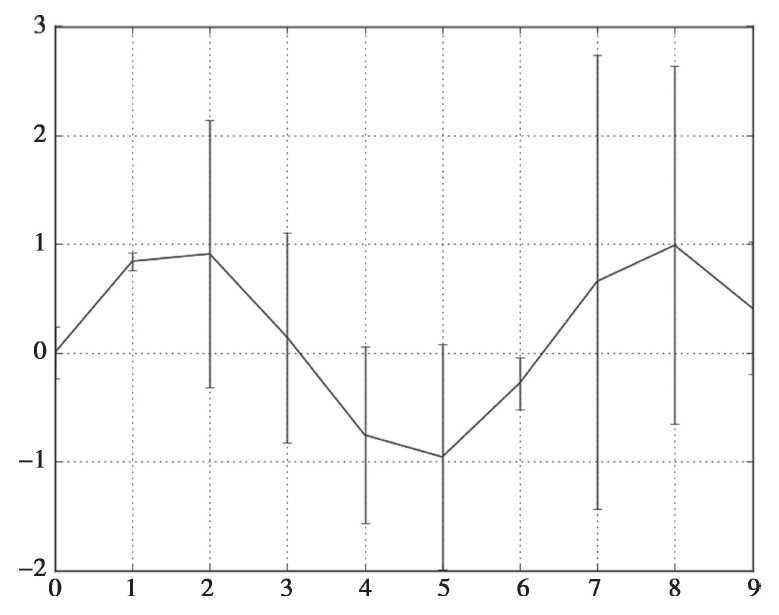
图　误差条形图

二、数据预处理

在数据挖掘中，海量的原始数据中存在着大量不完整（有缺失值）、不一致、有异常的数据，严重影响到数据挖掘建模的执行效率，甚至可能导致挖掘结果的偏差，所以进行数据清洗就显得尤为重要，数据清洗完成后接着进行或者同时进行数据集成、转换、归约等一系列处理，该过程就是数据预处理。数据预处理的目的一方面是提高数据的质量，另一方面是让数据更好地适应特定的挖掘技术或工具。统计发现，在数据挖掘过程中，数据预处理工作量占到了整个过程的60%。

数据预处理的主要内容包括数据清洗、数据集成、数据变换和数据归约。处理过程如图4-1所示。

2.1　数据清洗

数据清洗主要是删除原始数据集中的无关数据、重复数据，平滑噪声数据，筛选掉与挖掘主题无关的数据，处理缺失值、异常值等。

2.1.1　缺失值处理

处理缺失值的方法可分为3类：删除记录、数据插补和不处理。其中常用的数据插补方法如表所示。

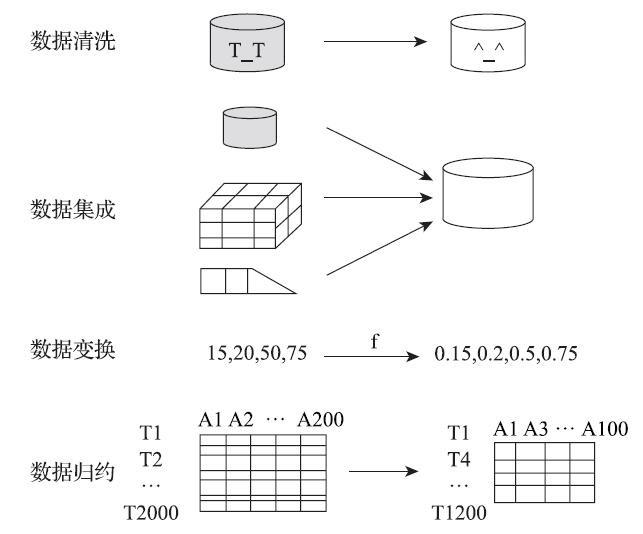
图　数据预处理过程示意图

表　常用的数据插补方法

如果简单地删除小部分记录就能达到既定的目标，那么删除含有缺失值的记录这种方法是最有效的。然而，这种方法却有很大的局限性。它是以减少历史数据来换取数据的完备，会造成资源的大量浪费，丢弃了大量隐藏在这些记录中的信息。尤其在数据集本来就包含很少记录的情况下，删除少量记录就可能严重影响分析结果的客观性和正确性。一些模型可以将缺失值视作一种特殊的取值，允许直接在含有缺失值的数据上进行建模。

（1）拉格朗日插值法

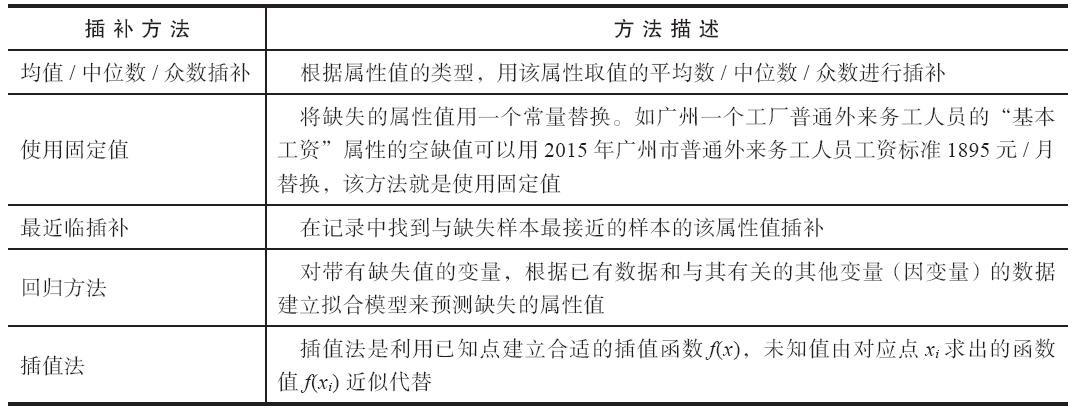
根据数学知识可知，对于平面上已知的n个点（无两点在一条直线上）可以找到一个n-1次多项式

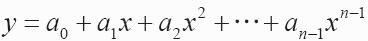
使此多项式曲线过这n个点。

求已知的过n个点的n-1次多项式如式所示。

将n个点的坐标（x1，y1），（x2，y2），…，（xn，yn）代入多项式函数，得式：

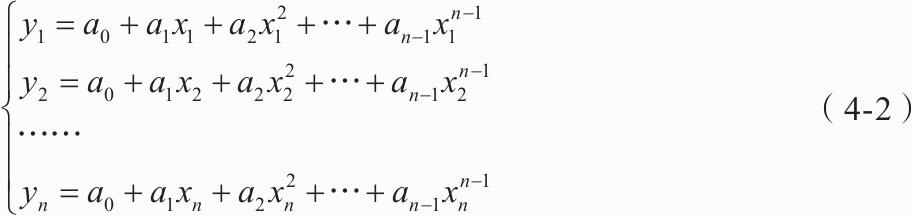
解得拉格朗日插值多项式为式（4-3）。

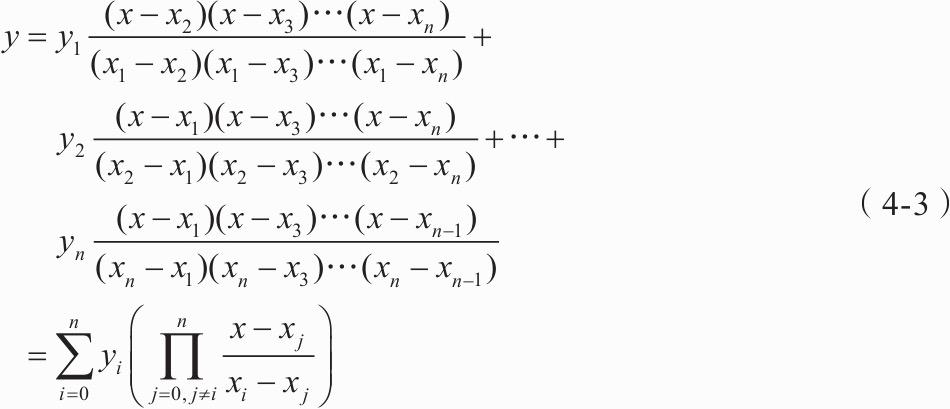
将缺失的函数值对应的点x代入插值多项式得到缺失值的近似值L(x)。

拉格朗日插值公式结构紧凑，在理论分析中使用方便，但是当插值节点增减时，插值多项式就会随之变化，这在实际计算中很不方便，为了克服这一缺点，提出了牛顿插值法。

（2）牛顿插值法

在区间[a，b]上，函数f(x)关于一个节点xi的零阶差商定义如式（4-4）所示，f(x)关于两个节点xi和xj的一阶差商定义见式（4-5）。一般地，k阶差商就是阶差商的差商，称式（4-6）为f(x)关于个节点x1，x2，…，xk的k阶差，具体可以按照表4-2的格式有规律地计算差商。

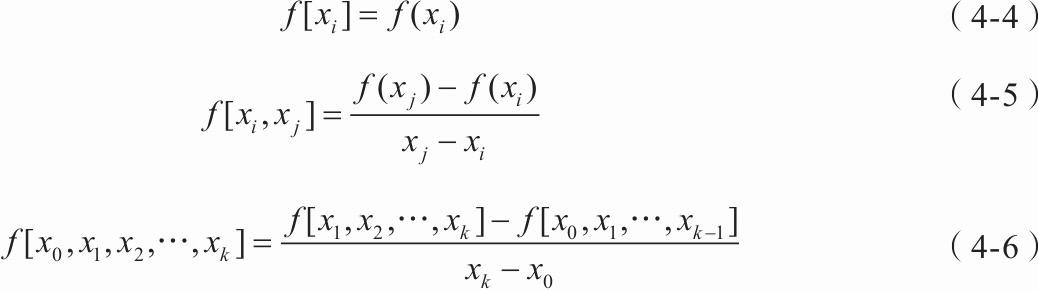
表4-2　差商表

借助差商的定义，牛顿插值多项式可以表示为式（4-7）

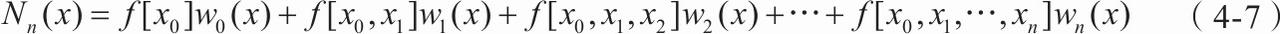
牛顿插值多项式的余项公式可以表示为式（4-8）。

其中，

对于区间[a，b]上的任一点x，则有。

牛顿插值法也是多项式插值，但采用了另一种构造插值多项式的方法，与拉格朗日插值相比，具有承袭性和易于变动节点的特点。本质上来说，两者给出的结果是一样的（相同次数、相同系数的多项式），只不过表示的形式不同。因此，在Python的SciPy库中，只提供了拉格朗日插值法的函数（因为比较容易实现）。如果需要牛顿插值法，则需要自行编写函数。

案例介绍拉格朗日插值法。

餐饮系统中的销量数据可能会出现缺失值，表4-3为某餐厅一段时间内的销量数据，其中2015年2月14日的数据缺失，用拉格朗日插值法对缺失值进行插补，如代码清单4-1所示。

表　某餐厅一段时间的销量数据

代码清单4-1　用拉格朗日插值法对缺失值进行插补

import pandas as pd                                           # 导入数据分析库pandas from scipy.interpolate import lagrange                        # 导入拉格朗日插值函数 inputfile = '../data/catering_sale.xls'                       # 销量数据路径 outputfile = '../tmp/sales.xls'                               # 输出数据路径 data = pd.read_excel(inputfile)                               # 读入数据 # 过滤异常值，将其变为空值 data['销量'][(data['销量'] < 400) | (data['销量'] > 5000)] = None # 自定义列向量插值函数 # s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5 def ployinterp_column(s, n, k=5):     y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))]        # 取数     y = y[y.notnull()]                                          # 剔除空值     return lagrange(y.index, list(y))(n)                        # 插值并返回插值结果 # 逐个元素判断是否需要插值 for i in data.columns:     for j in range(len(data)):         if (data[i].isnull())[j]:                               # 如果为空即插值             data[i][j] = ployinterp_column(data[i], j) data.to_excel(outputfile)                                       # 输出结果，写入文件

用拉格朗日插值法对表中的缺失值进行插补，使用缺失值前后各5个未缺失的数据参与建模，得到的插值结果如表所示。

表　数据插值结果

在进行插值之前会对数据进行异常值检测，发现2015年2月21日的数据是异常的（数据大于5000），所以也把该数据定义为空缺值，进行补数。利用拉格朗日插值法对2015年2月21和2015年2月14日的数据进行插补，结果分别是4275.255和4156.86，这两天都是周末，而周末的销售额一般要比周一到周五多，所以插值结果符合实际情况。

2.1.2　异常值处理

在数据预处理时，异常值是否剔除需视具体情况而定，因为有些异常值可能蕴含着有用的信息。异常值处理的常用方法见表。

表　异常值处理的常用方法

将含有异常值的记录直接删除，这种方法简单易行，但缺点也很明显，在观测值很少的情况下，直接删除会造成样本量不足，可能会改变变量的原有分布，从而造成分析结果的不准确。缺失值处理的好处是可以利用现有变量的信息，对异常值（缺失值）进行填补。

很多情况下，要先分析异常值出现的可能原因，再判断异常值是否应该舍弃。如果是正确的数据，可以直接在具有异常值的数据集上进行挖掘建模。

2.2　数据集成

数据挖掘需要的数据往往分布在不同的数据源中，数据集成就是将多个数据源合并存放在一个一致的数据存储位置（如数据仓库）中的过程。

在数据集成时，来自多个数据源的现实世界实体的表达形式是不一样的，有可能不匹配，要考虑实体识别问题和属性冗余问题，从而将源数据在最底层上加以转换、提炼和集成。

2.2.1　实体识别

实体识别是从不同数据源识别出现实世界的实体，它的任务是统一不同源数据的矛盾之处，常见的实体识别如下：

（1）同名异义

数据源A中的属性ID和数据源B中的属性ID分别描述的是菜品编号和订单编号，即描述的是不同的实体。

（2）异名同义

数据源A中的sales_dt和数据源B中的sales_date都是描述销售日期的，即A.sales_dt=B.sales_date。

（3）单位不统一

描述同一个实体时分别用的是国际单位和中国传统的计量单位。

检测和解决这些冲突就是实体识别的任务。

2.2.2　冗余属性识别

数据集成往往导致数据冗余，例如：

1）同一属性多次出现；

2）同一属性命名不一致导致重复。

仔细整合不同源数据能减少甚至避免数据冗余与不一致，从而提高数据挖掘的速度和质量。对于冗余属性要先进行分析，检测后再将其删除。

有些冗余属性可以用相关分析检测。给定两个数值型的属性A和属性B，根据其属性值，用相关系数度量一个属性在多大程度上蕴含另一个属性，相关系数介绍见3.2.6节。

2.3　数据变换

数据变换主要是对数据进行规范化处理，将数据转换成“适当的”形式，以适用于挖掘任务及算法的需要。

2.3.1　简单函数变换

简单函数变换是对原始数据进行某些数学函数变换，常用的包括平方、开方、取对数、差分运算等，分别如式（4-9）至式（4-12）所示。

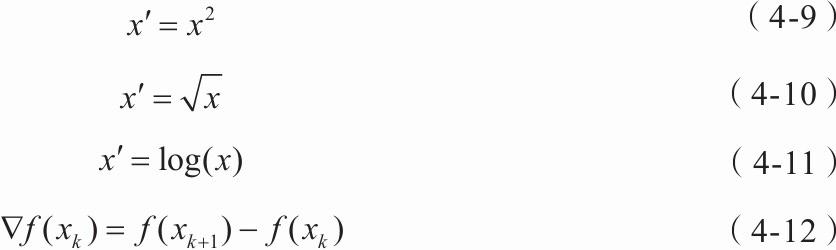
简单函数变换常用来将不具有正态分布的数据变换成具有正态分布的数据；在时间序列分析中，有时简单的对数变换或者差分运算就可以将非平稳序列转换成平稳序列。在数据挖掘中，简单函数变换可能更有必要，如个人年收入的取值范围为10000元到10亿元，这是一个很大的区间，使用对数变换对其进行压缩是常用的一种变换处理。

2.3.2　规范化

数据标准化（归一化）处理是数据挖掘的一项基础工作。不同评价指标往往具有不同的量纲，数值间的差别可能很大，不进行处理可能会影响数据分析的结果。为了消除指标之间的量纲和取值范围差异的影响，需要进行标准化处理，将数据按照比例进行缩放，使之落入一个特定的区域，便于进行综合分析。如将工资收入属性值映射到[-1，1]或者[0，1]内。

数据规范化对于基于距离的挖掘算法尤为重要。

（1）最小-最大规范化

最小-最大规范化也称为离差标准化，是对原始数据的线性变换，将数值映射到[0，1]之间。其转换公式如式（4-13）所示。

其中，max为样本数据的最大值，min为样本数据的最小值。max-min为极差。离差标准化保留了原来数据中存在的关系，是消除量纲和数据取值范围影响的最简单的方法。这种处理方法的缺点是：若数值集中且某个数值很大，则规范化后各值会接近于0，并且相差不大。若将来遇到超过目前属性[min，max]取值范围的时候，会引起系统出错，需要重新确定min和max。

（2）零-均值规范化

零-均值规范化也叫标准差标准化，经过处理的数据的均值为0，标准差为1。其转化公式如式（4-14）所示。

其中，为原始数据的均值，σ为原始数据的标准差。零-均值规范化是当前用得最多的数据标准化方法。

（3）小数定标规范化

通过移动属性值的小数位数，将属性值映射到[-1，1]之间，移动的小数位数取决于属性值绝对值的最大值。其转化公式如式（4-15）所示。

对于一个含有n个记录p个属性的数据集，就分别对每一个属性的取值进行规范化。对原始的数据矩阵分别用最小-最大规范化、零-均值规范化、小数定标规范化进行规范化，对比结果，如代码清单4-2所示。

代码清单4-2　数据规范化

import pandas as pd import numpy as np datafile = '../data/normalization_data.xls'          # 参数初始化 data = pd.read_excel(datafile, header=None)          # 读取数据 print(data) (data - data.min()) / (data.max() - data.min())      # 最小-最大规范化 (data - data.mean()) / data.std()                    # 零-均值规范化 data / 10 ** np.ceil(np.log10(data.abs().max()))     # 小数定标规范化 *代码详见：demo/code/data_normalization.py。

执行代码清单4-2后，得到的结果如下：

>>> print(data)      0    1    2     3 0   78  521  602  2863 1  144 -600 -521  2245 2   95 -457  468 -1283 3   69  596  695  1054 4  190  527  691  2051 5  101  403  470  2487 6  146  413  435  2571 >>> (data - data.min())/(data.max() - data.min())       # 最小-最大规范化           0         1         2         3 0  0.074380  0.937291  0.923520  1.000000 (data - data.min()) / (data.max() - data.min())      # 最小-最大规范化 (data - data.mean()) / data.std()                    # 零-均值规范化 data / 10 ** np.ceil(np.log10(data.abs().max()))     # 小数定标规范化 *代码详见：demo/code/data_normalization.py。 执行代码清单4-2后，得到的结果如下： >>> print(data)      0    1    2     3 0   78  521  602  2863 1  144 -600 -521  2245 2   95 -457  468 -1283 3   69  596  695  1054 4  190  527  691  2051 5  101  403  470  2487 6  146  413  435  2571 >>> (data - data.min())/(data.max() - data.min())       # 最小-最大规范化           0         1         2         3 0  0.074380  0.937291  0.923520  1.000000 1  0.619835  0.000000  0.000000  0.850941 2  0.214876  0.119565  0.813322  0.000000 3  0.000000  1.000000  1.000000  0.563676 4  1.000000  0.942308  0.996711  0.804149 5  0.264463  0.838629  0.814967  0.909310 6  0.636364  0.846990  0.786184  0.929571 >>> (data - data.mean())/data.std()                     # 零-均值规范化           0         1         2         3 0 -0.905383  0.635863  0.464531  0.798149 1  0.604678 -1.587675 -2.193167  0.369390 2 -0.516428 -1.304030  0.147406 -2.078279 3 -1.111301  0.784628  0.684625 -0.456906 4  1.657146  0.647765  0.675159  0.234796 5 -0.379150  0.401807  0.152139  0.537286 6  0.650438  0.421642  0.069308  0.595564 >>> data/10**np.ceil(np.log10(data.abs().max()))        # 小数定标规范化        0      1      2       3 0  0.078  0.521  0.602  0.2863 1  0.144 -0.600 -0.521  0.2245 2  0.095 -0.457  0.468 -0.1283 3  0.069  0.596  0.695  0.1054 4  0.190  0.527  0.691  0.2051 5  0.101  0.403  0.470  0.2487 6  0.146  0.413  0.435  0.2571

2.3.3　连续属性离散化

一些数据挖掘算法，特别是某些分类算法，如ID3算法、Apriori算法等，要求数据是分类属性形式。这样，常常需要将连续属性变换成分类属性，即连续属性离散化。

（1）离散化的过程

连续属性离散化就是在数据的取值范围内设定若干个离散的划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表落在每个子区间中的数据值。所以，离散化涉及两个子任务：确定分类数以及如何将连续属性值映射到这些分类值。

（2）常用的离散化方法

常用的离散化方法有等宽法、等频法和（一维）聚类。

等宽法

将属性的值域分成具有相同宽度的区间，区间的个数由数据本身的特点决定或者用户指定，类似于制作频率分布表。

等频法

将相同数量的记录放进每个区间。

这两种方法简单，易于操作，但都需要人为规定划分区间的个数。同时，等宽法的缺点在于它对离群点比较敏感，倾向于不均匀地把属性值分布到各个区间。有些区间包含许多数据，而另外一些区间的数据极少，这样会严重损坏建立的决策模型。等频法虽然避免了上述问题的产生，却可能将相同的数据值分到不同的区间，以满足每个区间中固定的数据个数。

基于聚类分析的方法

一维聚类方法包括两个步骤：首先将连续属性的值用聚类算法（如K-Means算法）进行聚类，然后再将聚类得到的簇进行处理，合并到一个簇的连续属性值做同一标记。聚类分析的离散化方法也需要用户指定簇的个数，从而决定产生的区间数。

下面使用上述3种离散化方法对“医学中中医证型的相关数据”进行连续属性离散化的对比，该属性的示例数据如表所示。

表　医学中中医证型的相关数据

对医学中中医证型的相关数据进行离散化，如代码清单4-3所示。

代码清单4-3　数据离散化

import pandas as pd import numpy as np datafile = '../data/discretization_data.xls'        # 参数初始化 data = pd.read_excel(datafile)        # 读取数据 data = data['肝气郁结证型系数'].copy() k = 4 d1 = pd.cut(data, k, labels=range(k))                  # 等宽离散化，各个类别依次命名为0,1,2,3 #等频率离散化 w = [1.0*i/k for i in range(k+1)] w = data.describe(percentiles=w)[4:4+k+1]          # 使用describe函数自动计算分位数 w[0] = w[0]*(1-1e-10) d2 = pd.cut(data, w, labels=range(k)) from sklearn.cluster import KMeans                  # 引入KMeans kmodel = KMeans(n_clusters=k, n_jobs=4)          # 建立模型，n_jobs是并行数，一般等 于CPU数较好 kmodel.fit(np.array(data).reshape((len(data), 1)))        # 训练模型 c = pd.DataFrame(kmodel.cluster_centers _).sort_values(0)                                                         # 输出聚类中心，并且排序（默认是随机排序的） w = c.rolling(2).mean()                                  # 相邻两项求中点，作为边界点 w = w.dropna() w = [0] + list(w[0]) + [data.max()]                  # 把首末边界点加上 d3 = pd.cut(data, w, labels=range(k)) def cluster_plot(d, k):                                  # 自定义作图函数来显示聚类结果     import matplotlib.pyplot as plt     plt.rcParams['font.sans-serif'] = ['SimHei']        # 用来正常显示中文标签     plt.rcParams['axes.unicode_minus'] = False          # 用来正常显示负号     plt.figure(figsize=(8, 3))     for j in range(0, k):         plt.plot(data[d==j], [j for i in d[d==j]], 'o')     plt.ylim(-0.5, k-0.5) return plt cluster_plot(d1, k).show() cluster_plot(d2, k).show() cluster_plot(d3, k).show()

运行代码清单4-3，可以得到图所示的结果。

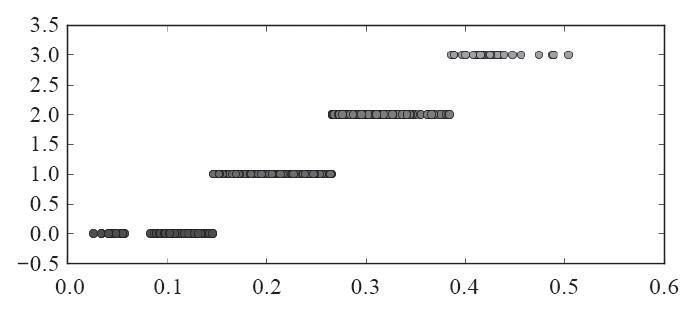
图　等宽离散化结果

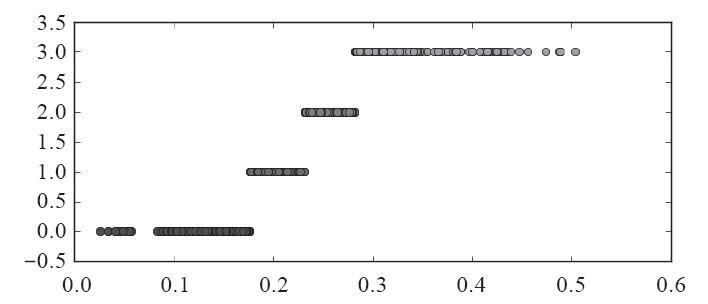
图　等频离散化结果

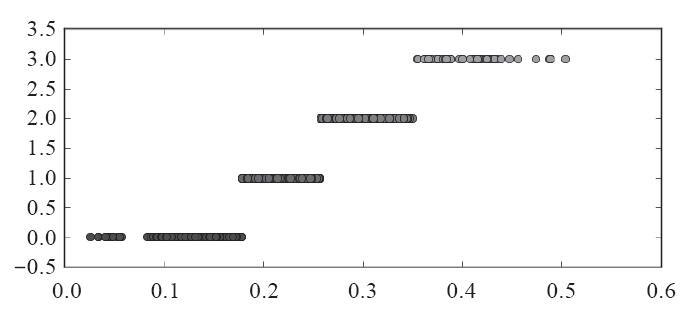
图　（一维）聚类离散化结果

分别用等宽法、等频法和（一维）聚类对数据进行离散化，将数据分成4类，然后将每一类记为同一个标识，如分别记为A1、A2、A3、A4，再进行建模。

2.3.4　属性构造

在数据挖掘过程中，为了帮助用户提取更有用的信息，挖掘更深层次的模式，提高挖掘结果的精度，需要利用已有的属性集构造出新的属性，并加入到现有的属性集合中。

例如，进行防窃漏电诊断建模时，已有的属性包括供入电量、供出电量（线路上各大用户用电量之和）。理论上供入电量和供出电量应该是相等的，但是由于在传输过程中存在电能损耗，使得供入电量略大于供出电量，如果该条线路上的一个或多个大用户存在窃漏电行为，会使得供入电量明显大于供出电量。反过来，为了判断是否有大用户存在窃漏电行为，可以构造出一个新的指标——线损率，该过程就是构造属性。新构造的属性线损率按式（4-16）计算。

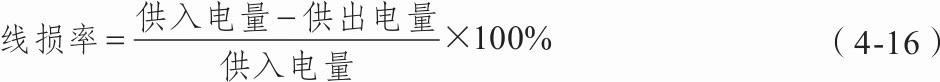
线损率的正常范围一般为3%～15%，如果远远超过该范围，那么就可以认为该条线路的大用户很可能存在窃漏电等异常用电行为。

根据线损率的计算公式，由供入电量、供出电量进行线损率的属性构造，如代码清单4-4所示。

代码清单4-4　线损率属性构造

import pandas as pd # 参数初始化 inputfile= '../data/electricity_data.xls'        # 供入供出电量数据 outputfile = '../tmp/electricity_data.xls'        # 属性构造后数据文件 data = pd.read_excel(inputfile)                          # 读入数据 data['线损率'] = (data['供入电量'] - data['供出电量']) / data['供入电量'] data.to_excel(outputfile, index=False)                # 保存结果

2.3.5　小波变换

小波变换是一种新型的数据分析工具，是近年来兴起的信号分析手段。小波分析的理论和方法在信号处理、图像处理、语音处理、模式识别、量子物理等领域得到了越来越广泛的应用，它被认为是近年来在工具及方法上的重大突破。小波变换具有多分辨率的特点，在时域和频域都具有表征信号局部特征的能力，通过伸缩和平移等运算过程对信号进行多尺度聚焦分析，提供了一种非平稳信号的时频分析手段，可以由粗及细地逐步观察信号，从中提取有用信息。

能够刻画某个问题的特征量往往隐含在一个信号中的某个或者某些分量中，小波变换可以把非平稳信号分解为表达不同层次、不同频带信息的数据序列，即小波系数，选取适当的小波系数，即完成了信号的特征提取。

（1）基于小波变换的特征提取方法

基于小波变换的特征提取方法主要有：基于小波变换的多尺度空间能量分布特征提取、基于小波变换的多尺度空间中模极大值特征提取、基于小波包变换的特征提取、基于适应性小波神经网络的特征提取，详见表。

表　基于小波变换的特征提取方法

（2）小波基函数

小波基函数是一种具有局部支集的函数，并且平均值为0。小波基函数满足。常用的小波基有Haar小波基、db系列小波基等。Haar小波基函数如图4-5所示。

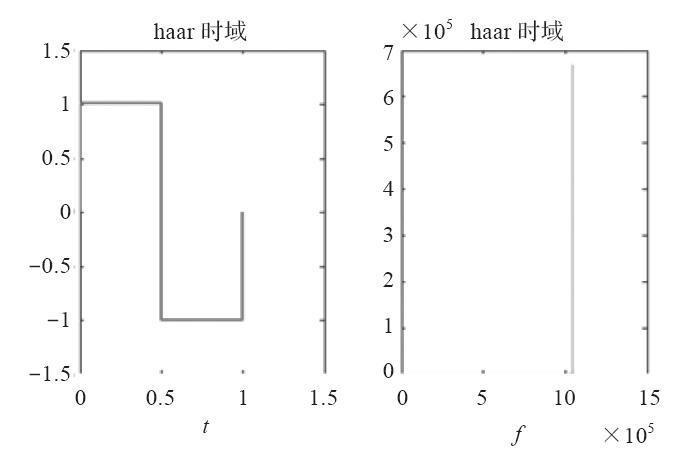
图　Haar小波基函数

（3）小波变换

对小波基函数进行伸缩和平移变换，如式（4-17）所示。

式（4-17）中，a为伸缩因子，b为平移因子。

任意函数f(t)的连续小波变换（CWT）为式（4-18）。

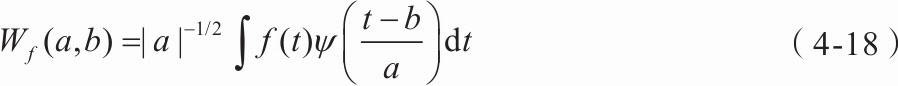
可知，连续小波变换为f(t)→Wf(a，b)的映射，对小波基函数ψ(t)增加约束条件

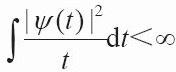
就可以由Wf(a，b)逆变换得到f(t)。其中ψ'(t)为ψ(t)的傅里叶变换。

其逆变换为式（4-19）。

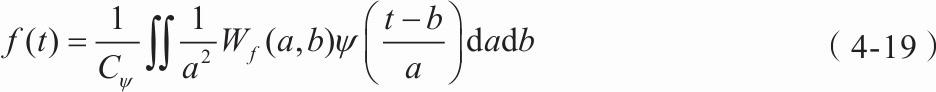
（4）基于小波变换的多尺度空间能量分布特征提取方法

应用小波分析技术可以把信号在各频率波段中的特征提取出来，基于小波变换的多尺度空间能量分布特征提取方法是对信号进行频带分析，再分别计算所得的各个频带的能量作为特征向量。

信号f(t)的二进小波分解可表示为式（4-20）。

式（4-20）中，A是近似信号，为低频部分；D是细节信号，为高频部分，此时信号的频带分布见图4-6。

信号的总能量为式（4-21）。

选择第j层的近似信号和各层的细节信号的能量作为特征，构造特征向量，如式（4-22）所示。

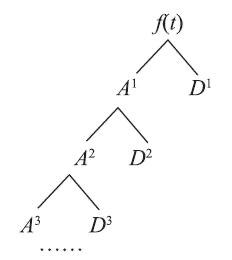
图　多尺度分解的信号频带分布

利用小波变换可以对声波信号进行特征提取，提取出可以代表声波信号的向量数据，即完成从声波信号到特征向量数据的变换。本例利用小波函数对声波信号数据进行分解，得到5个层次的小波系数。利用这些小波系数求得各个能量值，这些能量值即可作为声波信号的特征数据。

在Python中，SciPy本身提供了一些信号处理函数，但不够全面，而更好的信号处理库是PyWavelets。使用PyWavelets库进行小波变换，提取特征，如代码清单4-5所示。

代码清单4-5　小波变换特征提取代码

# 利用小波分析进行特征分析 # 参数初始化 inputfile= '../data/leleccum.mat'        # 提取自Matlab的信号文件 from scipy.io import loadmat          # mat是Python专用格式，需要用loadmat读取它 mat = loadmat(inputfile) signal = mat['leleccum'][0] import pywt  # 导入PyWavelets coeffs = pywt.wavedec(signal, 'bior3.7', level=5) # 返回结果为level+1个数字，第一个数组为逼近系数数组，后面的依次是细节系数数组

2.4　数据归约

在大数据集上进行复杂的数据分析和挖掘需要很长时间。数据归约产生更小且保持原数据完整性的新数据集，在归约后的数据集上进行分析和挖掘将提高效率。

数据归约的意义在于：

1）降低无效、错误数据对建模的影响，提高建模的准确性。

2）少量且具有代表性的数据将大幅缩减数据挖掘所需的时间。

3）降低储存数据的成本。

2.4.1　属性归约

属性归约通过属性合并创建新属性维数，或者通过直接删除不相关的属性（维）来减少数据维数，从而提高数据挖掘的效率，降低计算成本。属性归约的目标是寻找最小的属性子集并确保新数据子集的概率分布尽可能接近原来数据集的概率分布。属性归约常用方法见表。

表　属性归约常用方法

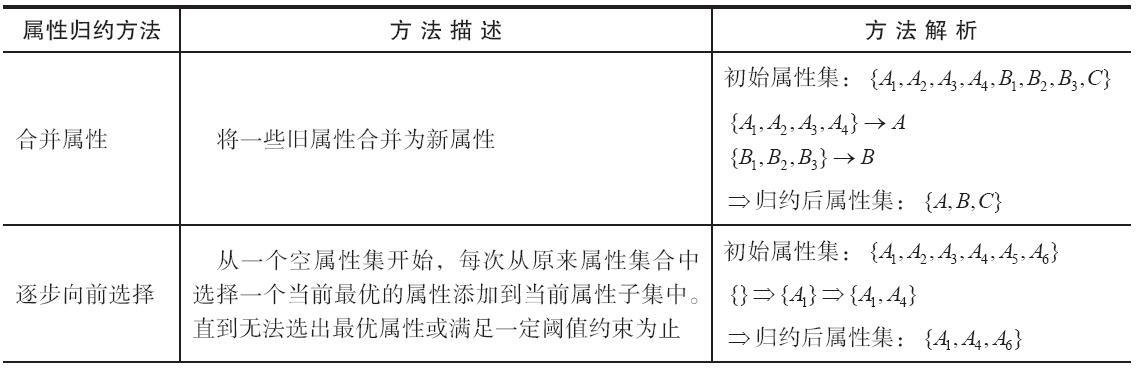
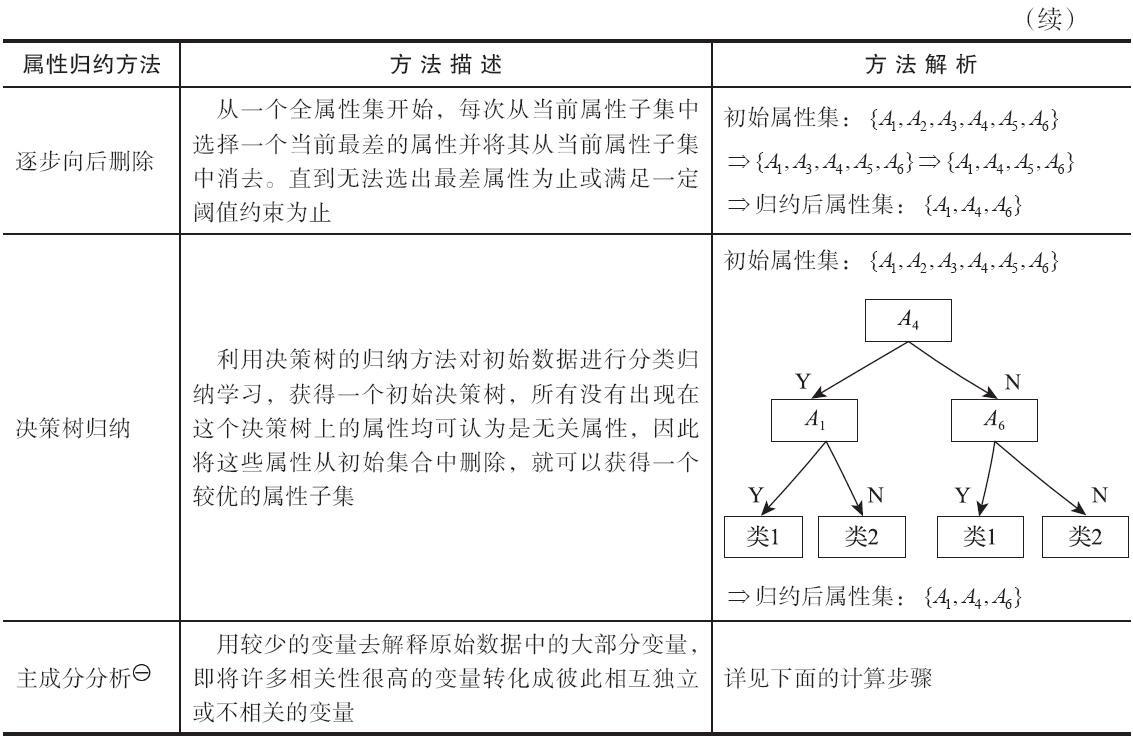
逐步向前选择、逐步向后删除和决策树归纳是属于直接删除不相关属性（维）的方法。主成分分析是一种用于连续属性的数据降维方法，它构造了原始数据的一个正交变换，新空间的基底去除了原始空间基底下数据的相关性，只需使用少数新变量就能够解释原始数据中的大部分变异。在应用中，通常是选出比原始变量个数少、能解释大部分数据中的变量的几个新变量，即所谓主成分，来代替原始变量进行建模。

主成分分析的计算步骤如下：

1）设原始变量X1，X2，…，Xp的n次观测数据矩阵为式（4-23）。

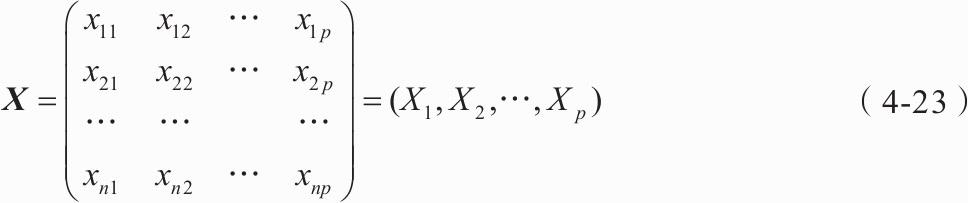
2）将数据矩阵按列进行中心标准化。为了方便，将标准化后的数据矩阵仍然记为X。

3）求相关系数矩阵R，

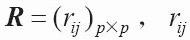
2）将数据矩阵按列进行中心标准化。为了方便，将标准化后的数据矩阵仍然记为X。

3）求相关系数矩阵R，

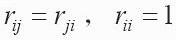
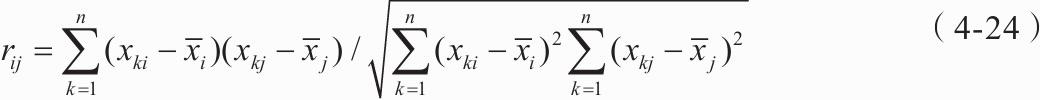
4）求R的特征方程det(R-λE)=0的特征根。

5）确定主成分个数m：

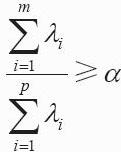
α根据实际问题确定，一般取80%。

6）计算m个相应的单位特征向量，如式（4-25）所示。

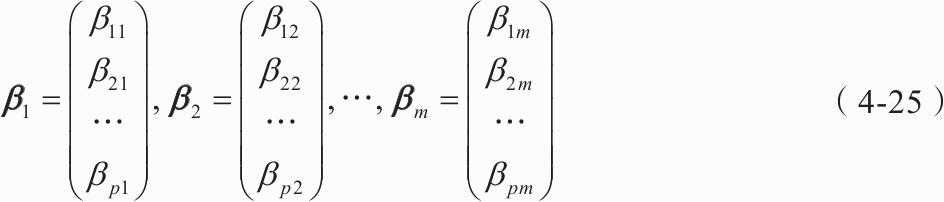
7）计算主成分，如式（4-26）所示。

在Python中，主成分分析的函数位于scikit-learn库下，其使用格式如下，参数说明如表4-9所示。

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)

表　PCA函数的参数说明

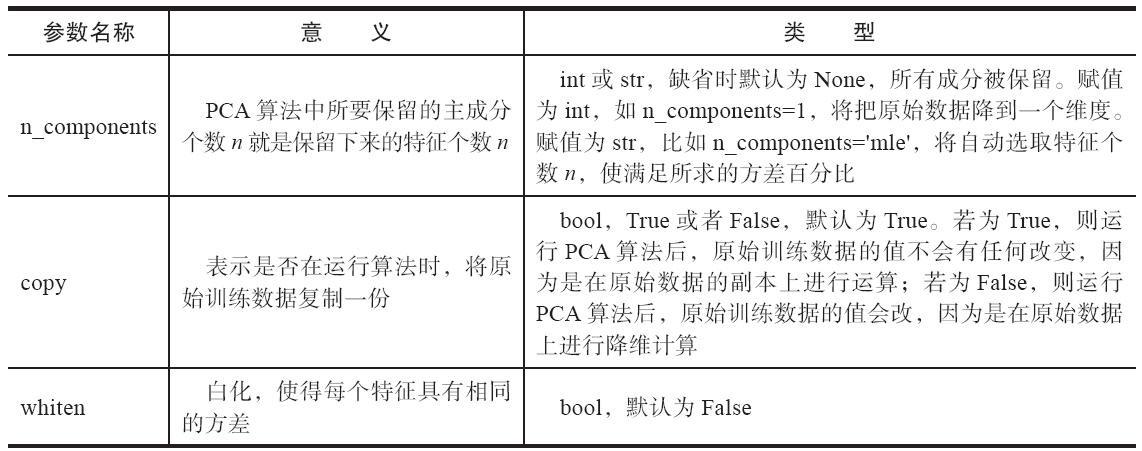
使用主成分分析法进行降维，如代码清单4-6所示。

代码清单4-6　主成分分析法降维

import pandas as pd # 参数初始化 inputfile = '../data/principal_component.xls' outputfile = '../tmp/dimention_reducted.xls'          # 降维后的数据 data = pd.read_excel(inputfile, header=None)          # 读入数据 from sklearn.decomposition import PCA pca = PCA() pca.fit(data) pca.components_                                        # 返回模型的各个特征向量 pca.explained_variance_ratio_                          # 返回各个成分各自的方差百分比

运行代码清单4-6得到的结果如下：

>>> pca.components_                  # 返回模型的各个特征向量 array([[-0.56788461, -0.2280431 , -0.23281436, -0.22427336, -0.3358618 ,         -0.43679539, -0.03861081, -0.46466998],        [-0.64801531, -0.24732373,  0.17085432,  0.2089819 ,  0.36050922,          0.55908747, -0.00186891, -0.05910423],        [-0.45139763,  0.23802089, -0.17685792, -0.11843804, -0.05173347,  -0.20091919, -0.00124421,  0.80699041],        [-0.19404741,  0.9021939 , -0.00730164, -0.01424541,  0.03106289,          0.12563004,  0.11152105, -0.3448924 ],        [ 0.06133747,  0.03383817, -0.12652433, -0.64325682,  0.3896425 ,          0.10681901, -0.63233277, -0.04720838],        [-0.02579655,  0.06678747, -0.12816343,  0.57023937,  0.52642373,         -0.52280144, -0.31167833, -0.0754221 ],        [ 0.03800378, -0.09520111, -0.15593386, -0.34300352,  0.56640021,         -0.18985251,  0.69902952, -0.04505823],        [ 0.10147399, -0.03937889, -0.91023327,  0.18760016, -0.06193777,          0.34598258,  0.02090066, -0.02137393]]) >>> pca.explained_variance_ratio_        # 返回各个成分各自的方差百分比（贡献率） array([  7.74011263e-01,   1.56949443e-01,   4.27594216e-02,          2.40659228e-02,   1.50278048e-03,   4.10990447e-04,          2.07718405e-04,   9.24594471e-05])

从上面的结果可以得到特征方程det(R-λE)=0有8个特征根、对应的8个单位特征向量以及各个成分各自的方差百分比（也叫贡献率）。其中方差百分比越大说明向量的权重越大。

当选取前4个主成分时，累计贡献率已达到97.37%，说明选取前3个主成分进行计算已经相当不错了，因此可以重新建立PCA模型，设置n_components=3，计算出成分结果，如代码清单4-7所示。

代码清单4-7　计算成分结果

pca = PCA(3) pca.fit(data) low_d = pca.transform(data)                  # 用它来降低维度 pd.DataFrame(low_d).to_excel(outputfile)     # 保存结果 pca.inverse_transform(low_d)                 # 必要时可以用inverse_transform()函数来复原数据

运行代码清单4-7得到的结果如下：

>>> low_d array([[ -8.19133694, -16.90402785,   3.90991029],        [ -0.28527403,   6.48074989,  -4.62870368],        [ 23.70739074,   2.85245701,  -0.4965231 ],        [ 14.43202637,  -2.29917325,  -1.50272151],        [ -5.4304568 , -10.00704077,   9.52086923],        [-24.15955898,   9.36428589,   0.72657857],        [  3.66134607,   7.60198615,  -2.36439873],        [-13.96761214, -13.89123979,  -6.44917778],        [-40.88093588,  13.25685287,   4.16539368],        [  1.74887665,   4.23112299,  -0.58980995],        [ 21.94321959,   2.36645883,   1.33203832],        [ 36.70868069,   6.00536554,   3.97183515],        [ -3.28750663,  -4.86380886,   1.00424688],        [ -5.99885871,  -4.19398863,  -8.59953736]])

原始数据从8维被降维到了3维，关系式由式（4-26）确定，同时这3维数据占了原始数据95%以上的信息。

2.4.2　数值归约

数值归约通过选择替代的、较小的数据来减少数据量，包括有参数方法和无参数方法两类。有参数方法是使用一个模型来评估数据，只需存放参数，而不需要存放实际数据，例如回归（线性回归和多元回归）和对数线性模型（近似离散属性集中的多维概率分布）。无参数方法就需要存放实际数据，例如直方图、聚类、抽样（采样）。

（1）直方图

直方图使用分箱来近似数据分布，是一种流行的数据归约形式。属性A的直方图将A的数据分布划分为不相交的子集或桶。如果每个桶只代表单个属性值/频率对，则该桶称为单桶。通常，桶表示给定属性的一个连续区间。

这里结合实际案例来说明如何使用直方图做数值归约。某餐饮企业菜品的单价（按人民币取整）从小到大排序为：3，3，5，5，5，8，8，10，10，10，10，15，15，15，22，22，22，22，22，22，22，22，22，25，25，25，25，25，25，25，25，25，30，30，30，30，30，35，35，35，35，35，39，39，40，40，40。使用单桶显示这些数据的直方图如图4-7所示。为进一步压缩数据，通常让每个桶代表给定属性的一个连续值域。在图4-8中，每个桶代表长度为13元（人民币）的价值区间。

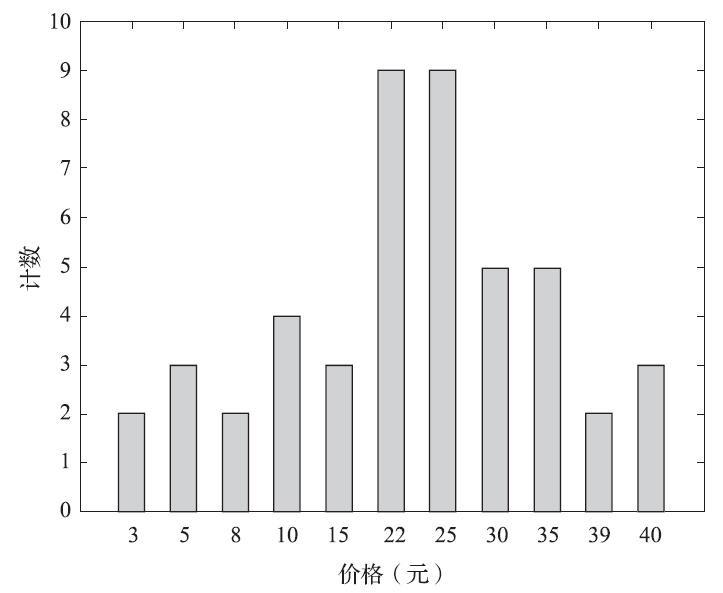
图　使用单桶的价格直方图——每个单桶代表一个价值/频率对

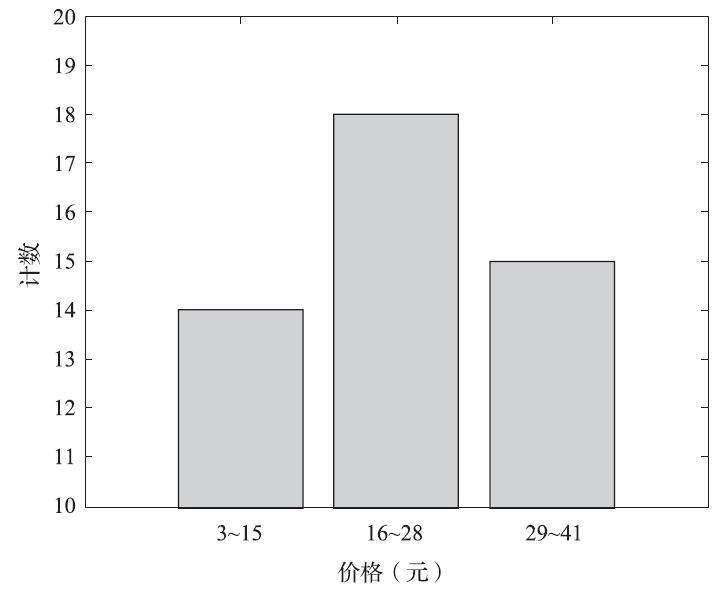
图　价格的等宽直方图——每个桶代表一个价格区间/频率对

（2）聚类

聚类技术将数据元组（即记录，数据表中的一行）视为对象。它将对象划分为簇，使一个簇中的对象彼此“相似”，而与其他簇中的对象“相异”。在数据归约中，用数据的簇替换实际数据。该技术的有效性依赖于簇的定义是否符合数据的分布性质。

（3）抽样

抽样也是一种数据归约技术，它用比原始数据小得多的随机样本（子集）表示原始数据集。假定原始数据集D包含n个元组，可以采用抽样方法对原始数据集D进行抽样。下面介绍常用的抽样方法。

s个样本无放回简单随机抽样

从原始数据集D的n个元组中抽取s个样本（s＜n），其中D中任意元组被抽取的概率均为1/N，即所有元组的抽取是等可能的。

s个样本有放回地简单随机抽样

该方法类似于无放回简单随机抽样，不同之处在于每次从原始数据集D中抽取一个元组后，做好记录，然后放回原处。

聚类抽样

如果原始数据集D中的元组分组放入m个互不相交的“簇”，则可以得到s个簇的简单随机抽样，其中s＜m。例如，数据库中的元组通常一次检索一页，这样每页就可以视为一个簇。

分层抽样

如果原始数据集D划分成互不相交的部分，称作层，则通过对每一层的简单随机抽样就可以得到D的分层样本。例如，按照顾客的每个年龄组创建分层，可以得到关于顾客数据的一个分层样本。

使用数据归约时，抽样最常用来估计聚集查询的结果。在指定的误差范围内，可以确定（使用中心极限定理）一个给定的函数所需的样本大小。通常样本的大小s相对于n非常小。而通过简单地增加样本大小，这样的集合可以进一步求精。

参数回归

简单线性模型和对数线性模型可以用来近似给定的数据。用（简单）线性模型对数据建模，使之拟合一条直线。下面介绍一个简单线性模型的例子，对对数线性模型只做简单介绍。

例如，把点（2，5），（3，7），（4，9），（5，12），（6，11），（7，15），（8，18），（9，19），（11，22），（12，25），（13，24），（15，30），（17，35）归约成线性函数。即拟合函数线上对应的点可以近似看作已知点。如图4-9所示。

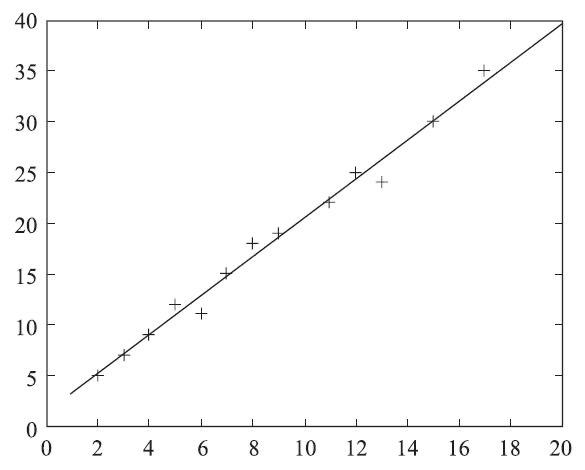
图　将已知点归约成线性函数y=wx+b

其中，y的方差是常量13.44。在数据挖掘中，x和y是数值属性。系数2和1.3（称作回归系数）分别为直线的斜率和y轴截距。系数可以用最小二乘方法求解，可以使数据的实际直线与估计直线之间的误差最小化。多元线性回归是（简单）线性回归的扩充，允许响应变量y建模为两个或多个预测变量的线性函数。

对数线性模型：用来描述期望频数与协变量（指与因变量有线性相关并在探讨自变量与因变量关系时通过统计技术加以控制的变量）之间的关系。考虑期望频数m在正无穷之间，故需要将对数变换为f(m)=ln m，使它的取值在-∞与+∞之间。

对数线性模型为式（4-27）。

对数线性模型一般用来近似离散多维概率分布。在一个n元组的集合中，每个元组可以看作是n维空间中的一个点。可以使用对数线性模型基于维组合的一个较小子集，估计离散化的属性集的多维空间中每个点的概率，这使得高维数据空间可以由较低维空间来构造。因此，对数线性模型也可以用于维归约（由于低维空间的点通常比原来的数据点占据较少的空间）和数据光滑（因为与较高维空间的估计相比，较低维空间的聚集估计较少受抽样方差的影响）。

2.5　Python主要数据预处理函数

表给出了本节要介绍的Python中的插值、数据归一化、主成分分析等与数据预处理相关的函数。下面对它们进行详细介绍。

表　Python主要数据预处理函数

（1）interpolate

功能：interpolate是SciPy的一个子库，下面包含了大量的插值函数，如拉格朗日插值、样条插值、高维插值等。使用之前需要用from scipy.interpolate import*引入相应的插值函数，读者可以根据需要到官网查找对应的函数名。

使用格式：f = scipy.interpolate.lagrange(x, y)

这里仅仅展示了一维数据的拉格朗日插值的命令，其中x，y为对应的自变量和因变量数据。插值完成后，可以通过f(a)计算新的插值结果。类似的还有样条插值、多维数据插值等，此处不一一展示。

（2）unique

功能：去除数据中的重复元素，得到单值元素列表。它既是NumPy库的一个函数（numpy.unique()），也是Series对象的一个方法。

使用格式：numpy.unique(D) 其中D是一维数据，可以是list、array或Series。

D.unique() 其中D是pandas的Series对象。

实例

求向量D中的单值元素，并返回相关索引，如代码清单4-8所示。

代码清单4-8　求向量D中的单值元素，并返回相关索引

import pandas as pd import numpy as np D = pd.Series([1, 1, 2, 3, 5]) D.unique() np.unique(D)

（3）isnull/notnull

功能：判断每个元素是否空值/非空值。

使用格式：D.isnull()/D.notnull()

这里的D要求是Series对象，返回一个布尔Series。可以通过D[D.isnull()]或D[D.notnull()]找出D中的空值/非空值。

（4）random

功能：random是NumPy的一个子库（Python本身也自带了random，但NumPy的random更加强大），可以用该库下的各种函数生成服从特定分布的随机矩阵，抽样时可使用。

使用格式：np.random.rand(k, m, n, ...) 生成一个k×m×n×…随机矩阵，其元素均匀分布在区间(0，1)上。

np.random.randn(k, m, n, ...) 生成一个k×m×n×…随机矩阵，其元素服从标准正态分布。

（5）PCA

功能：对指标变量矩阵进行主成分分析。使用前需要用from scipy.interpolate import*引入相应的插值函数。

使用格式：model = PCA()

注意，scikit-learn下的PCA是一个建模式的对象，也就是说一般的流程是建模，然后是训练model.fit(D)，D为要进行主成分分析的数据矩阵，训练结束后获取模型的参数，如.components_获取特征向量，.explained_variance_ratio_获取各个属性的贡献率等。

实例

使用PCA函数对一个10×4维的随机矩阵进行主成分分析，如代码清单4-9所示。

代码清单4-9　对一个10×4维的随机矩阵进行主成分分析

from sklearn.decomposition import PCA D = np.random.rand(10,4) pca = PCA() pca.fit(D) pca.components_                       # 返回模型的各个特征向量 pca.explained_variance_ratio_         # 返回各个成分各自的方差百分比