聚类概述

一、什么是聚类

聚类是将数据对象的集合分成相似的对象类的过程。使得同一个簇（或类）中的对象之间具有较高的相似性，而不同簇中的对象具有较高的相异性。

二、相似性测度

1、距离相似性度量

曼哈坦距离

欧几里得距离

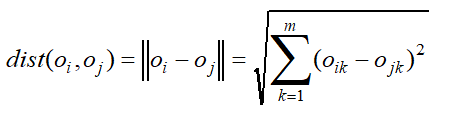
闵可夫斯基距离

2、密度相似性度量

密度是单位区域内的对象个数。密度相似性度量定义为：

density(Ci，Cj)=|di－dj|

其中di、dj表示簇Ci、Cj的密度。其值越小，表示密度越相近，Ci、Cj相似性越高。这样情况下，簇是对象的稠密区域，被低密度的区域环绕。

3、连通性相似性度量

数据集用图表示，图中结点是对象，而边代表对象之间的联系，这种情况下可以使用连通性相似性，将簇定义为图的连通分支，即图中互相连通但不与组外对象连通的对象组。

也就是说，在同一连通分支中的对象之间的相似性度量大于不同连通分支之间对象的相似性度量。

4、概念相似性度量

若聚类方法是基于对象具有的概念，则需要采用概念相似性度量，共同性质（比如最近邻）越多的对象越相似。簇定义为有某种共同性质的对象的集合。 

5、其他相似性度量

（1）夹角余弦

用两个向量oi和oj之间的余弦作为相似系数，取值范围为[0,1]。当两个向量正交时，取值为0，表示两个对象完全不相似。

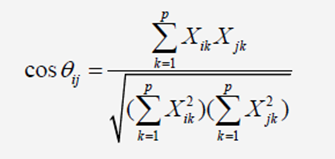
（2）相关系数法

该方法计算两个向量之间的相关系数,取值范围为[-1，1]，其中0表示两个向量互相独立，1表示两个向量正相关，-1表示两个向量负相关。

三、聚类方法的分类

1、按照聚类的尺度，聚类方法可被分为以下三种：

基于距离的聚类算法：用各式各样的距离来衡量数据对象之间的相似度。

基于密度的聚类算法：相对于基于距离的聚类算法，基于密度的聚类方法主要是依据合适的密度函数等。

基于互连性的聚类算法：通常基于图或超图模型。高度连通的对象聚为一类。

2、按照聚类分析方法的主要思路，可以被归纳为如下几种

划分法：基于一定标准构建数据的划分。

层次法：对给定数据对象集合进行层次的分解。

密度法：基于数据对象的相连密度评价。

网格法：将数据空间划分成为有限个单元的网格结构，基于网格结构进行聚类。

模型法：给每一个簇假定一个模型，然后去寻找能够很好的满足这个模型的数据集。