Apriori算法

Apriori算法是由Agrawal等人于1993提出的，它采用逐层搜索策略（层次搜索策略）产生所有的频繁项集。 

一、Apriori性质

Apriori性质：若A是一个频繁项集，则A的每一个子集都是一个频繁项集。

例如，若{beer，diaper，nuts}项集是频繁的，则{beer，diaper}也一定是频繁的，但{apple，beer，diaper，nuts}不一定是频繁的。

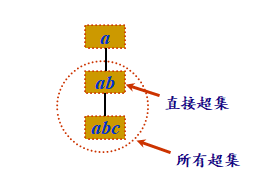
定义5.8 一个项集A的超集C，是指C满足AÌC，且|A|<|C|。也就是说，由A项集添加任意多个其他项构成的项集都是A的超集。

　由项集A仅添加一个项构成的项集C称为A的直接超集。注意这里在A中添加的项默认都是不重复的项。

二、Apriori算法

1. 基本的Apriori算法

Apriori算法的基本思路是采用层次搜索的迭代方法，由候选(k-1)-项集来寻找候选k-项集，并逐一判断产生的候选k-项集是否是频繁的。

　设Ck是长度为k的候选项集的集合，Lk是长度为k的频繁项集的集合。为了简单，设最小支持度阈值min_sup为最小元组数，即采用最小支持度计数。

首先，找出频繁1-项集，用L1表示。

由L1寻找C2，由C2产生L2，即产生频繁2-项集的集合。

由L2寻找C3，由C3产生L3。

以此类推，直至没有新的频繁k-项集被发现。求每个Lk时都要对事务数据库D作一次完全扫描。

【例5.1】对于表5.1所示的事务数据库，设min_sup=2，产生所有频繁项集的过程如图5.1所示，最后L4=Ф，算法结束，产生的所有频繁项集为L1∪L2∪L3。

解体见视频

2. 自连接：由Lk-1构建Ck

为找出Lk，通过Lk-1与自身连接产生候选k-项集的集合，记作Ck。设l1和l2是Lk-1中的项集。li[j]表示li的第j项。假定事务或项集中的项按字典次序排序，使得li[1]<li[2]<...<li[k-1]。执行连接Lk-1       Lk-1；其中Lk-1的元素是可连接的，如它们前（k-2）个项相同，即Lk-1的元素l1和l2是可连接的，如（l1[1]=l2[1]）Ù（l1[2]=l2[2]）Ù...Ù（l1[k-2]＝l2[k-2]）Ù（l1[k-1]<l2[k-1]）。条件l1[k-1]<l2[k-1]是简单地确保不产生重复。连接l1和l2产生的结果项集是｛l1[1]，l1[2]，...l1[k-1]，l2[k-1]｝

例如：由L2生成C3的过程中，L2中的{A,C}和{B,C}只相差一个项目，因此它们可以连接生成{A,B,C}。

但是， L2中的{A,C}和{B,E}无法进行连接。

3. 对Ck进行剪枝操作

对于由Lk-1生成的Ck，从Ck中删除明显不是频繁项集的项集，这称为剪枝操作。这里Lk-1包含所有的(k-1)-频繁项集，也就是说，若某个(k-1)-项集不在Lk-1中，则它一定不是频繁的。

Apriori算法的性质：频繁集的所有非空子集也一定是频繁的。

例如：虽然L2中的{A,C}和{B,C}可以连接生成{A,B,C}，但是由于{A,B,C}的子集{A,B}不是频繁集(不在L2中)，因此，需要从C3中删除{A,B,C} 。

三、由频繁项集产生关联规则

1. 产生关联规则的基本过程

因为由频繁项集的项组成的关联规则的支持度大于等于最小支持度阈值，所以规则产生过程是：

　在由频繁项集的项组成的所有关联规则中，找出所有置信度大于等于最小置信度阈值的强关联规则。

对于形如lu→(l-lu)的规则，其置信度为 

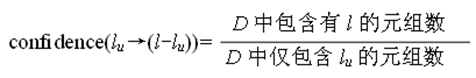
因此，对于每个频繁项集l，求强关联规则的基本步骤如下：

①产生l的所有非空真子集。

②对于l的每个非空真子集lu，如果l的支持度计数除以lu的支持度计数大于等于最小置信度阈值min_conf，则输出强关联规则lu→(l-lu)。其中，因为l是频繁项集，根据Apriori性质，lu与(l-lu)都是频繁项集，所以，其支持计数在频繁项集产生阶段已经计算，在此不必重复计算。

2. 通过剪枝提高效率

对于频繁项集l及其两个非空真子集lu和lv，如果lvÍlu，并且规则lu→(l-lu)不是强关联规则，则规则lv→(l-lv)也不是强关联规则。

生成强关联规则的剪枝原则：

由于lu和lv是l的两个非空真子集，所以lvÍlu等价于(l-lv)Ê(l-lu)，也就是说，若(l-lv)Ê(l-lu)成立，并且规则lu→(l-lu)不是强关联规则，则规则lv→(l-lv)也不是强关联规则。

更简单地说，对于频繁项集l，在产生它的所有强关联规则时，若l的某个真子集la，有(l-la)→la不是强关联规则，则对于后件为la的超集的任何规则均不是强关联规则。

四、非二元属性的关联规则挖掘

现实数据集中的属性通常可以取离散化的多个值，甚至是连续值，无法直接利用上述算法挖掘出关联规则。

　为此可以利用数据预处理方法，将它们转换为二元属性，再应用针对购物篮数据的关联规则挖掘算法。

具体内容见视频