【数据及分析对象】CSV文件——文件名为“Online Retail.xlsx”，数据内容来自“在线零售数据集”，下载地址为https://archive.ics.uci.edu/ml/datasets/online+retail。该数据集记录了2010年12月01日至2011年12月09日的541909条在线交易记录，包含以下8个属性。

· InvoiceNo：订单编号，由6位整数表示，退货单号由字母“C”开头。

· StockCode：产品编号，每个不同的产品由不重复的5位整数表示。

· Description：产品描述。

· Quantity：产品数量，每笔交易的每件产品的数量。

· InvoiceDate：订单日期和时间，表示生成每笔交易的日期和时间。

· UnitPrice：单价，单个产品的英镑价格。

· CustomerID：顾客编号，每位客户由唯一的5位整数表示。

· Country：国家名称，每位客户所在国家/地区的名称。

【目的及分析任务】理解Apriori算法的具体应用。

1）计算最小支持度为0.07的德国客户购买产品的频繁项集。

2）计算最小置信度为0.8且提升度不小于2的德国客户购买产品的关联关系。

【方法及工具】能够实现Aprior算法的Python第三方工具包有mlxtend、kiwi-apriori、apyori、apriori_python、efficient-apriori等，比较常用的是mlxtend、apriori_python、efficient-apriori，本节采用的是mlxtend包。

一、业务理解

本例所涉及的业务为购物篮分析，即计算德国客户购买产品的频繁项集和关联关系，从而判断哪些商品更可能被同时购买。该业务的主要内容是将最小支持度设为0.07，生成德国客户购买产品的频繁项集，并计算德国客户购买产品中具有正相关关系的商品，并将最小置信度设为0.8，筛选出满足最小置信度且提升度不小于2的德国客户购买产品的关联关系。

该业务所涉及的业务术语为购物篮分析，指从单个客户一次购买商品的数据信息中挖掘商品之间的关联关系，进而辅助决策者调整营销策略。

二、数据读入

安装mlxtend的命令：condau install-Cu Condaforgeu mlxtend

首先，导入本案例所需的Python包：

将数据读入并存为dataframe格式，查看前5行数据：

对应输出结果为：

其中unicode_escape编码方式表示在Python的源代码中将unicode的内存编码值直接进行存储。

三、数据理解

调用shape属性查看数据框df_Retails的形状：

对应输出结果为：

可知该数据集共有541909行8列。查看8列的列名称：

对应输出结果为：

接下来对数据框df_Retails进行探索性分析，本例首先调用describe（）方法。

对应输出结果为：

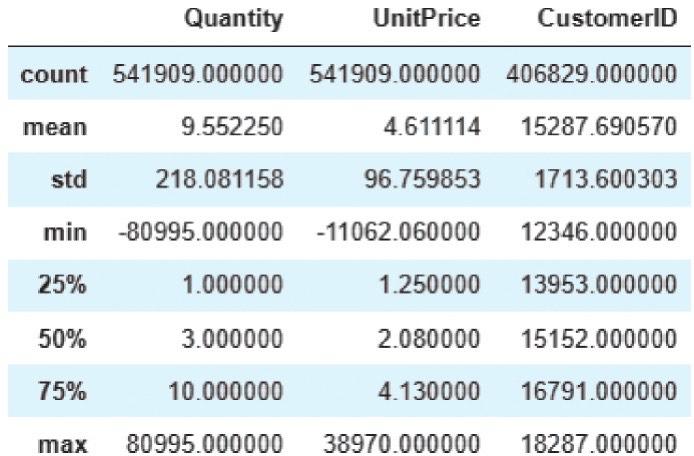
其中，count、mean、std、min、25%、50%、75%和max的含义分别为个数、均值、标准差、最小值、上四分位数、中位数、下四分位数和最大值。

除了describe（）方法，还可以调用info（）方法查看样本数据的相关信息概览：

对应输出结果为：

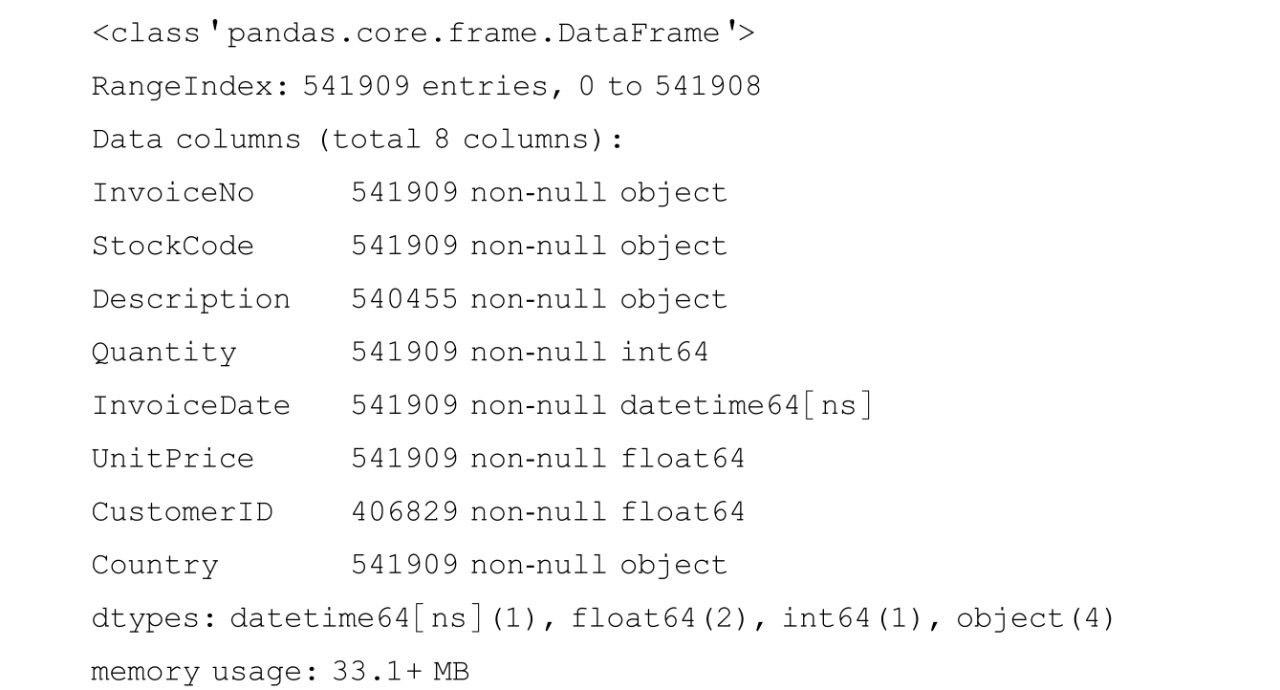
从此输出结果可看出，数据框df_Retails的Description和CustomerID两列有缺失值。

看国家一列的取值：

对应输出结果为：

查看各国家的购物数量：

对应输出结果为：

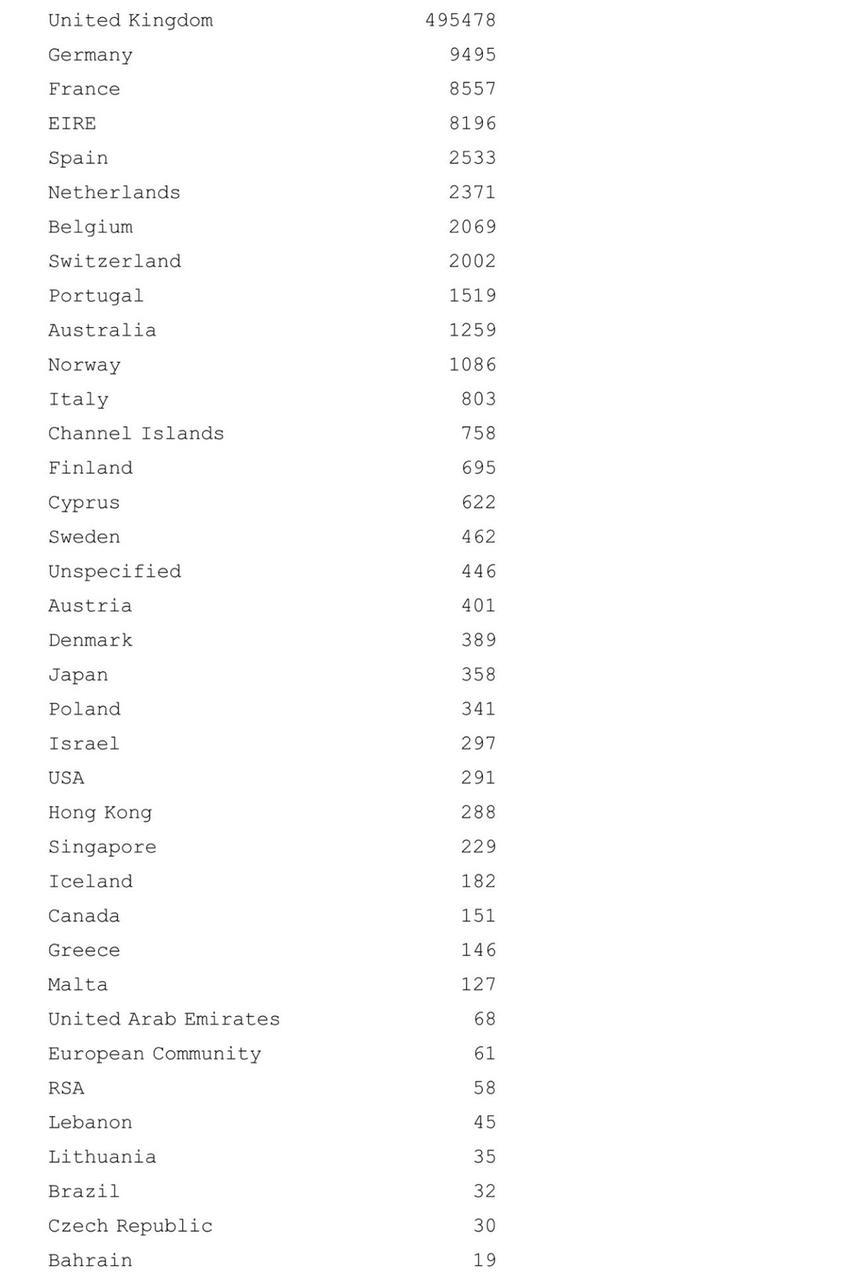
可以看出，英国的客户购买商品数量最多，为495478条记录，其次是德国的客户，为9495条记录。

查看订单编号（InvoiceNo）一列中是否有重复的值：

对应输出结果为：

订单编号有重复表示同一个订单中有多个同时购买的产品，符合Apriori算法的数据要求。

四、数据预处理

查看数据集中是否有缺失值。

对应输出结果为：

可以看出，Description的缺失值有1454条，CustomerID的缺失值有135080条。

将商品名称（Description）一列的字符串头尾的空白字符删除：

再次查看数据集形状：

对应输出结果为：

该数据集仍为541909行8列。查看商品名称（Description）一列的缺失值个数：

对应输出结果为：

在对商品名称（Description）一列进行空白字符处理后，缺失值增加了一个。去除所有的缺失值：

再次查看数据集形状：

对应输出结果为：

经过去除缺失值处理的数据集由541909变为540454行。检查此时的数据集是否还有缺失值：

对应输出结果为：

   可以看出，数据框df_Retails中商品名称（Description）一列的缺失值已全部被删除。由于退货的订单编号由字母“C”开头，删除含有C字母的已取消订单：

再次查看数据集形状：

对应输出结果为：

将数据改为每一行一条购物记录，并考虑到内存限制以及德国（Germany）的购物数量位居第二，因此在本案例中只计算德国客户购买的商品的频繁项集及关联规则，全部计算则计算量太大。

对应输出结果为：

德国的购物记录共有457条，共包含1695件不同的商品。查看df_ShoppingCarts的前5行：

对应输出结果为：

查看订单编号（InvoiceNo）一列是否有重复的值：

对应输出结果为：

订单编号有重复表示同一个订单中有多个同时购买的产品，符合Apriori算法的数据要求。由于apriori方法中df参数允许的值为0/1或True/False，在此将这些项在数据框中转换为0/1的形式，即转换为模型可接受格式的数据即可进行频繁项集和关联度的计算。

五、生成频繁项集

mlxtend.frequent_patterns的apriori（）方法可进行频繁项集的计算，将最小支持度设定为0.07：

对应输出结果为：

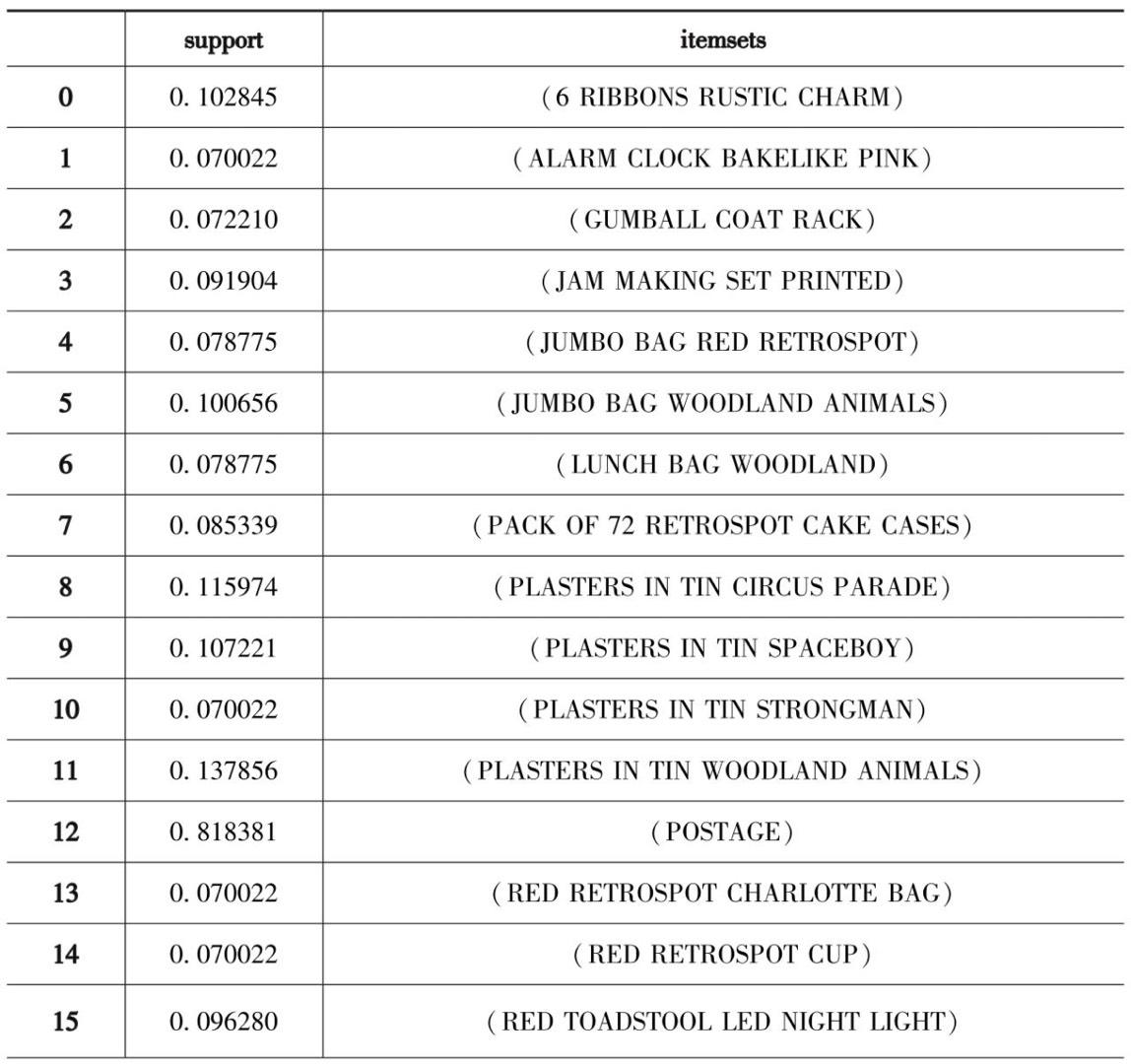
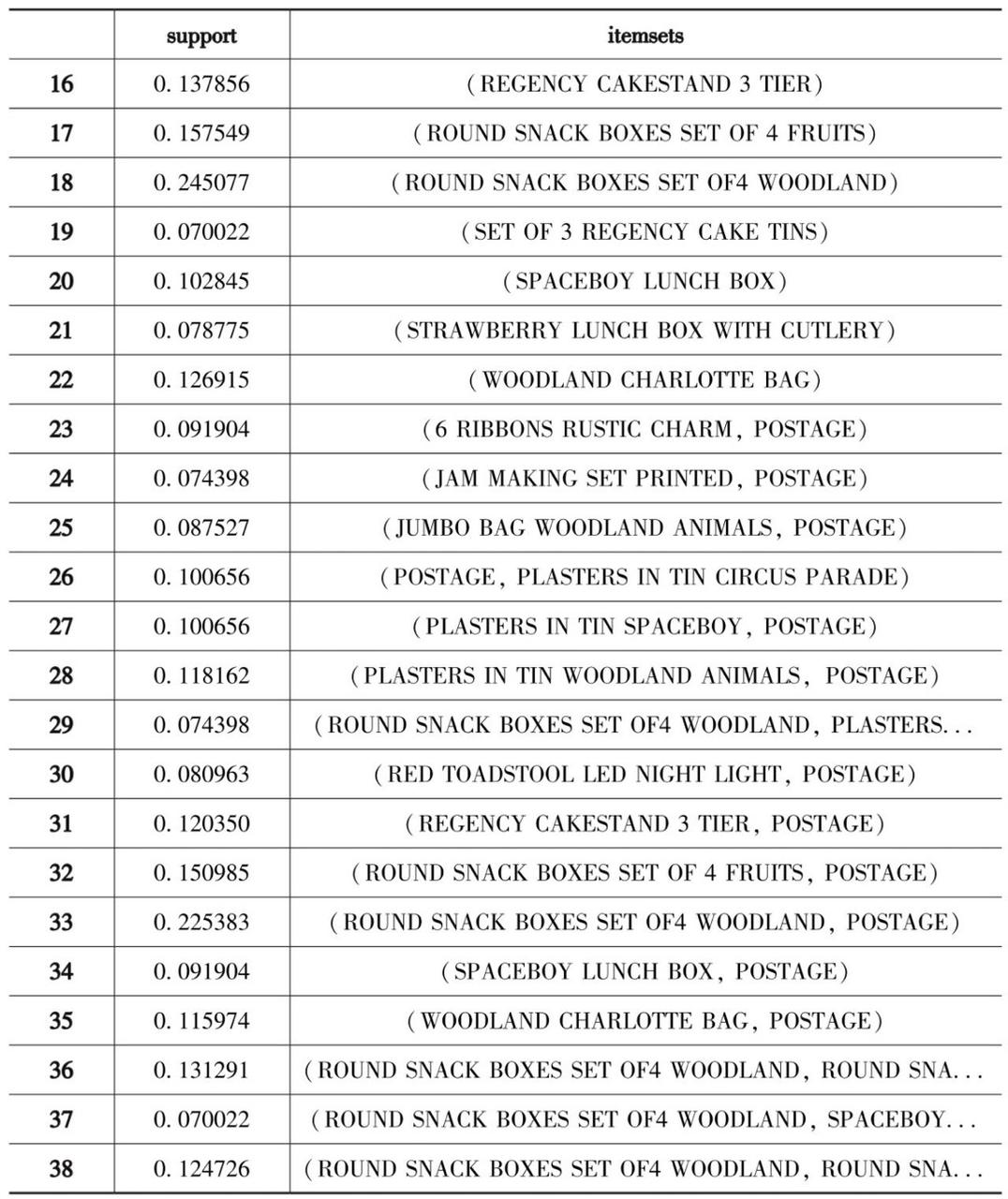
查看数据框df_Frequent_Itemsets的形状：

对应输出结果为：

可以看出，满足最小支持度0.07的频繁项集为38个。

六、计算关联度

将提升度（lift）作为度量计算关联规则，并设置阈值为1，表示计算具有正相关关系的关联规则。该任务由mlxtend.frequent_patterns的association_rules（）方法实现：

对应输出结果为：

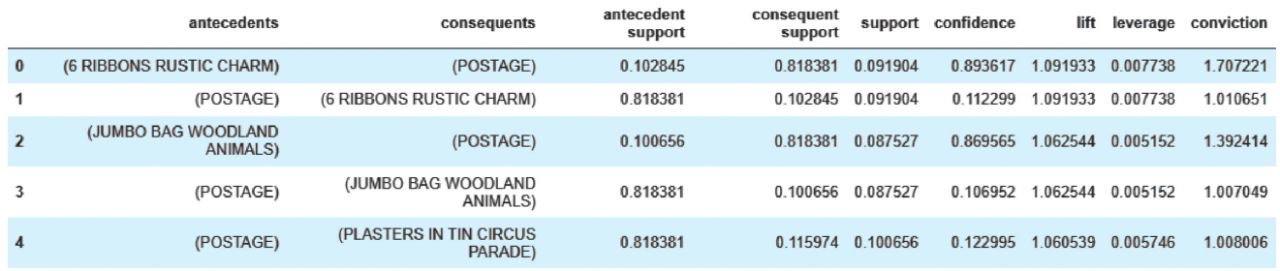
从结果可以看出各项关联规则的详细信息。以第一条关联规则{6 RIBBONS RUSTIC CHARM}→{POSTAGE}为例，{6 RIBBONS RUSTIC CHARM}的支持度为0.102845，{POSTAGE}的支持度为0.818381，项集{6 RIBBONS RUSTIC CHARM，POSTAGE}的支持度为0.091904，客户购买6 RIBBONS RUSTIC CHARM时也购买POSTAGE的置信度为0.893617，提升度为1.091933，规则杠杆率（即当6 RIBBONS RUSTIC CHARM和POSTAGE独立分布时，6 RIBBONS RUSTIC CHARM和POSTAGE一起出现的次数比预期多）为0.007738，规则确信度（与提升度类似，但用差值表示，确信度值越大则6 RIBBONS RUSTIC CHARM和POSTAGE关联关系越强）为1.707221。

查看数据框df_AssociationRules的形状：

对应输出结果为：

可以看出，总共输出了34条关联规则。接着筛选出提升度不小于2且置信度不小于0.8的关联规则：

对应输出结果为：

由此可知提升度不小于2且满足最小置信度0.8的强关联规则有两条，分别为：{ROUND SNACK BOXES SET OF 4 FRUITS}→{ROUND SNACK BOXES SET OF4 WOODLAND}和{ROUND SNACK BOXES SET OF 4 FRUITS，POSTAGE}→{ ROUND SNACK BOXES SET OF4 WOODLAND}。

七、可视化

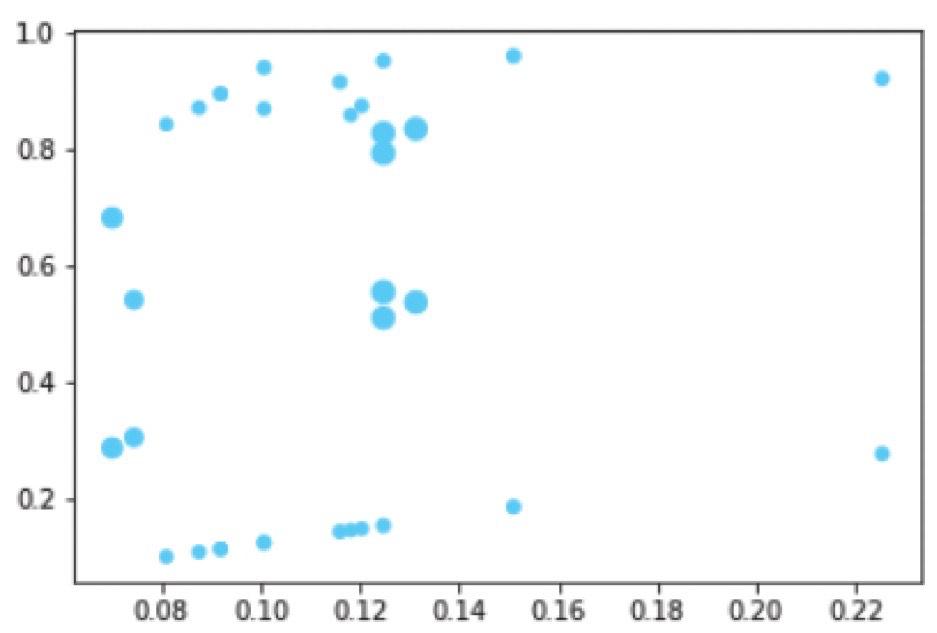
绘制出提升度不小于1的关联规则的散点图，横坐标设置为支持度，纵坐标为置信度，散点的大小表示提升度。该可视化任务由matplotlib.pyplot的scatter函数实现：

对应输出结果如图2-5所示。

八、重点与难点解读

表2-1给出了apriori超参数及其解读，表2-2给出了association_rules超参数及其解读。

表2-1 apriori超参数及其解读

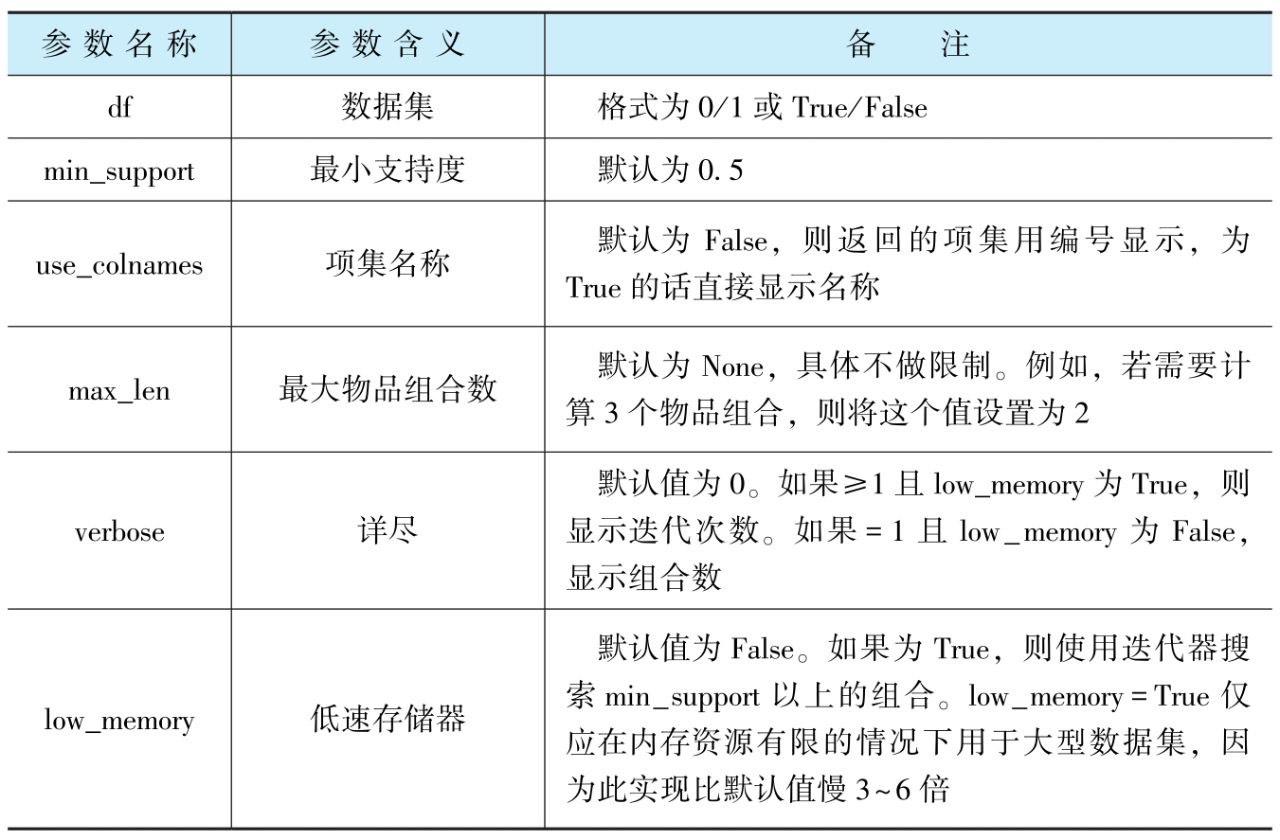
表2-2 association_rules超参数及其解读

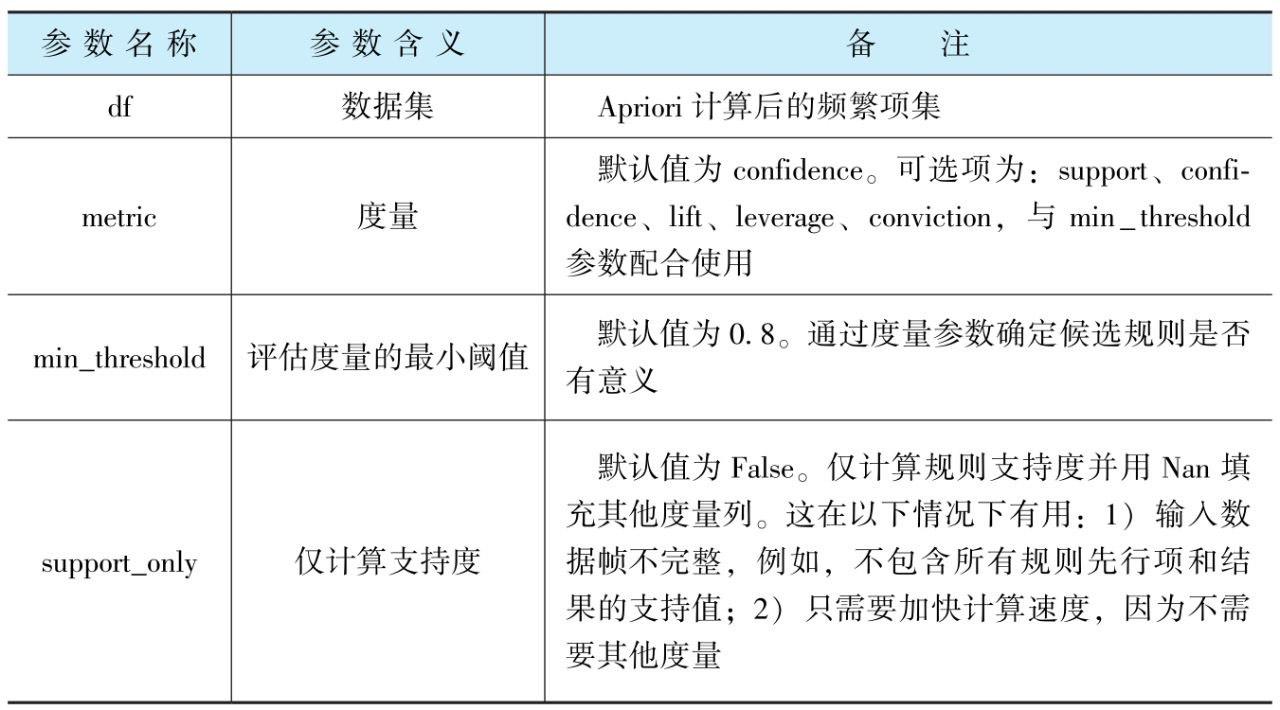
其中，参数metric不同可选值的范围不同，其计算方式及取值范围也不同。对规则A→C而言：