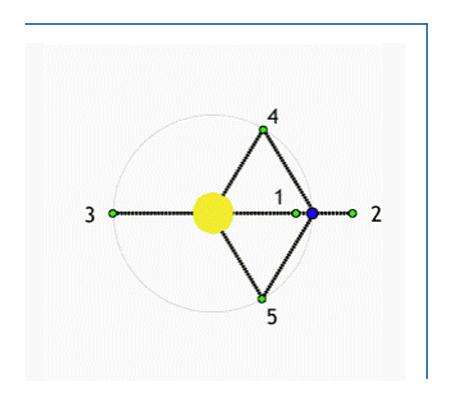
拉格朗日点，又称平动点，在天体力学中是限制性三体问题的五个特解。一个小物体在两个大物体的引力作用下在空间中的一点，在该点处，小物体相对于两大物体基本保持静止。这些点的存在由瑞士数学家欧拉于1767年推算出前三个，法国数学家拉格朗日于1772年推导证明剩下两个。1906年首次发现运动于木星轨道上的小行星（见特洛依群小行星）在木星和太阳的作用下处于拉格朗日点上。在每个由两大天体构成的系统中，按推论有5个拉格朗日点，但只有两个是稳定的，即小物体在该点处即使受外界引力的摄扰，仍然有保持在原来位置处的倾向。每个稳定点同两大物体所在的点构成一个等边三角形。

1906年首次发现运动于木星轨道上的小行星（见特洛依群小行星）在木星和太阳的作用下处于拉格朗日

点上。在每个由两大天体构成的系统中，按推论有5个拉格朗日点，但只有两个是稳定的，即小物体在该点处即使受外界引力的摄扰，仍然有保持在原来位置处的倾向。每个稳定点同两大物体所在的点构成一个等边三角。

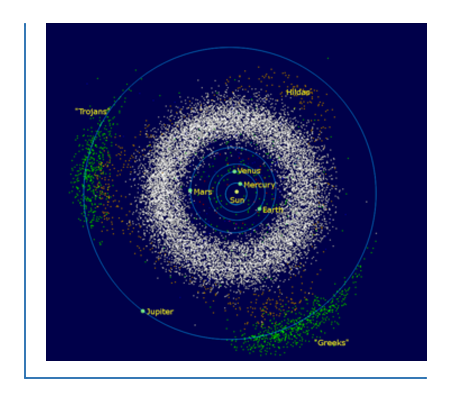
18世纪法国数学家、力学家和天文学家拉格朗日（拉格朗治）在1772年发表的论文“三体问题”中，为了求得三体问题的通解，他用了一个非常特殊的例子作为问题的结果，即：如果某一时刻，三个运动物体恰恰处于等边三角形的三个顶点，那么给定初速度，它们将始终保持等边三角形队形运动。A.D 1906年，天文学家发现了第588号小行星和太阳正好等距离，它同木星几乎在同一轨道上超前60°运动，它们一起构成运动着的等边三角形。同年发现的第617号小行星也在木星轨道上落后60°左右，构成第2个拉格朗日（拉格朗治）正三角形。20世纪80年代，天文学家发现土星和它的大卫星构成的运动系统中也有类似的正三角形。人们进一步发现，在自然界各种运动系统中，都有拉格朗日（拉格朗治）点。