拉普拉斯-龙格-楞次矢量

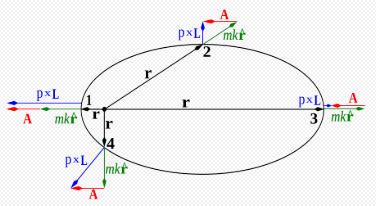
在经典力学里，拉普拉斯-龙格-楞次矢量（简称为LRL 矢量）主要是用来描述，当一个物体环绕着另外一个物体运动时，轨道的形状与取向。典型的例子是行星的环绕着太阳公转。在一个物理系统里，假若两个物体以万有引力相互作用，则 LRL 矢量必定是一个运动常数，不管在轨道的任何位置，计算出来的 LRL 矢量都一样；也就是说， LRL 矢量是一个保守量。更广义地，在开普勒问题里，由于两个物体以有心力相互作用，而有心力遵守平方反比定律，所以，LRL 矢量是一个保守量。

在一个物理系统里，在任意保守的有心力的作用下，一个粒子的运动，都会拥有至少四个运动常数；能量与角动量L的三个分量皆为运动常数。粒子的轨道被限制于一个平面。粒子的动量P和从力中心点的位置到粒子位置的位移r。粒子的运动平面垂直于角动量L。用方程表示，LRL矢量A，也肯定地包含于粒子的运动平面。可是，只有当有心力遵守平方反比定律时，A才是常数矢量。对于别种有心力，A不是常数矢量，其大小与方向都会改变。假若有心力近似地遵守平方反比定律，则A的大小近似常数，而方向会缓慢地转动。对于所有的有心力，可以定义一个广义LRL矢量，但是，这广义矢量通常并没有解析解，假若有，也会是一个非常复杂的函数。

数学定义

 平方反比有心力可以表达为  

其中，k是比例常数，   是单位矢量，r是粒子的位置矢量。

感受到此力的作用，一个粒子的轨道运动，其LRL矢量的数学定义方程为 

其中，m是粒子的质量，p是动量，L是角动量。

由于平方反比有心力为保守力，能量是运动常数：

再者，角动量L也是保守的，可以决定粒子移动平面的取向。因为  与r都垂直于L，所以，LRL矢量A垂直于角动量；A包含于轨道的平面。

这个单独粒子的LRL矢量定义，也可以延伸至像开普勒问题一类的二体问题，只需要设定质量m为二个物体的约化质量，设定位置矢量r为二个物体之间的相对位置矢量。

同样的运动常数可以有很多种不同的表述．最常见的一种牵涉到离心率矢量。定义离心率矢量e为LRL矢量与mk的除商：