开普勒定律

开普勒定律是德国天文学家开普勒提出的关于行星运动的三大定律。第一和第二定律发表于1609年，是开普勒从天文学家第谷观测火星位置所得资料中总结出来的；第三定律发表于1619年。这三大定律又分别称为椭圆定律、面积定律和调和定律。

① 椭圆定律所有行星绕太阳的轨道都是椭圆，太阳在椭圆的一个焦点上。

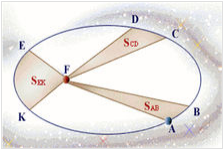
② 面积定律行星和太阳的连线在相等的时间间隔内扫过相等的面积。

③ 调和定律所有行星绕太阳一周的恒星时间(  )的平方与它们轨道长半轴(ai)的立方成比例，即  。

此后，学者们把第一定律修改成为：所有行星（和彗星）的轨道都属于圆锥曲线，而太阳则在它们的一个焦点上。第二定律只在行星质量比太阳质量小得多的情况下才是精确的。如果考虑到行星也吸引太阳，这便是一个二体问题。经过修正后的第三定律的精确公式为：  

 （式中m1和m2为两个行星的质量；ma为太阳的质量）。

数学推导

开普勒定律是关于行星环绕太阳的运动，而牛顿定律更广义的是关于几个粒子因万有引力相互吸引而产生的运动。在只有两个粒子，其中一个粒子超轻于另外一个粒子，这些特别状况下，轻的粒子会环绕重的粒子移动，就好似行星根据开普勒定律环绕太阳的移动。然而牛顿定律还容许其它解答，行星轨道可以呈抛物线运动或双曲线运动。这是开普勒定律无法预测到的。在一个粒子并不超轻于另外一个粒子的状况下，依照广义二体问题的解答，每一个粒子环绕它们的共同质心移动。这也是开普勒定律无法预测到的。

开普勒定律，或者是用几何语言，或者是用方程，将行星的坐标及时间跟轨道参数相连结。牛顿第二定律是一个微分方程。开普勒定律的导引涉及解微分方程的艺术。我们会先导引开普勒第二定律，因为开普勒第一定律的导引必须建立于开普勒第二定律。

第一定律的证明 

设定   这样，角速度是  

对时间微分和对角度微分有如下关系：

根据上述关系，径向距离 对时间的导数为：

再求一次导数：

代入径向运动方程

 ，

将此方程除以  ，则可得到一个简单的常系数非齐次线性全微分方程来描述行星轨道：

为了解这个微分方程，先列出一个特解 

再求解剩余的常系数齐次线性全微分方程， 

它的解为 

这里，  与  是常数。合并特解和与齐次方程解，可以得到通解 

选择坐标轴，让  。代回   ，

其中，   是离心率。

这是圆锥曲线的极坐标方程，坐标系的原点是圆锥曲线的焦点之一。假若  ，则  所描述的是椭圆轨道。这证明了开普勒第一定律。 

第二定律的证明

开普勒第二定律是这么说的：在相等的时间内，行星与恒星的连线扫过的面积相等。O为恒星，直线AC为行星不受引力时的轨迹。设行星从A到B、从B到C所用的时间间隔Δt相等，A处的时刻为t1，B为t2，C为t3。假设行星不受O的引力作用，那么这时扫过的面积SΔABO和SΔBCO相等（等底同高）。行星受到引力作用了，因为引力的方向时刻指向恒星，所以在从t1到t3这段

时间里，行星所受的引力的方向的总效果应该沿着BO方向（这需要一点向量的知识）。因此，t3时刻行星的位置C’应该由两个向量相加而得到：向量AC+向量CC’（作CC’平行于BO，因此沿BO方向的向量等价于CC’）。这样，SΔBCO=SΔBC’O(同底等高)。因此，SΔBC’O=SΔABO。因为Δt是任取的，所以在相等的时间内，行星与恒星的连线扫过的面积相等。

第三定律的证明 

在图中，A，B分别为行星运动的近日点和远日点，以  和  分别表示行星在该点的速度，由于速度沿轨道切线方向，可见  和  的方向均与此椭圆的长轴垂直，则行星在此两点时对应的面积速度分别为

 ……………………………………{1}

根据开普勒第二定律，应有  ，因此得

 ……………………………………………{2}

行星运动的总机械能E等于其动能与势能之和，则当他经过近日点和远日点时，其机械能应分别为

 …………{3}

根据机械能守恒，应有  ，故得

 ……………………{4}

由{2}{4}两式可解得

 ………………………………{5}

由{5}式和{1}式得面积速度为

椭圆的面积为  ,则得此行星运动周期为

 …………………………{6}

将{6}式两边平方，便得

注：  是半长轴，  是半短轴，  是半焦距