芝诺佯谬

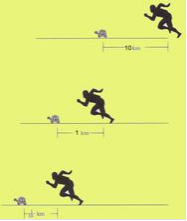
芝诺悖论（Zeno's paradox）是古希腊数学家芝诺（Zeno of Elea）提出的一系列关于运动的不可分性的哲学悖论。

这些悖论由于被记录在亚里士多德的《物理学》一书中而为后人所知。芝诺提出这些悖论是为了支持他老师巴门尼德关于“存在”不动、是一的学说。这些悖论中最著名的两个是：“阿基里斯跑不过乌龟”和“飞矢不动”。这些方法可以用微积分（无限）的概念解释，但还是无法用微积分解决，因为微积分原理存在的前提是存在广延（如，有广延的线段经过无限分割，还是由有广延的线段组成，而不是由无广延的点组成。），而芝诺悖论中既承认广延，又强调无广延的点。这些悖论之所以难以解决，是因为它集中强调后来笛卡尔和伽桑迪为代表的机械论的分歧点。 

芝诺

芝诺（Zeno of Elea）生于意大利半岛南部的埃利亚城邦，他是埃利亚学派的著名哲学家巴门尼德（Parmenides）的学生和朋友。据说他在母邦度过了一生，仅在成名之后到过雅典。据传说，芝诺因蓄谋反对埃利亚（另一说为叙拉古）的僭主，而被拘捕、拷打，直至处死。关于他的生平，缺乏可靠的文字记载。

柏拉图在他的对话《巴门尼德篇》中，记载了芝诺和巴门尼德于公元前5世纪中叶去雅典的一次访问。其中有这样的文字：“巴门尼德年事已高，约65岁；头发很白，但仪表堂堂。那时的芝诺约40岁，身材魁梧而美观，大家说他已经变成巴门尼德所钟爱的了。”在以后的希腊著作家看来，这次访问是柏拉图虚构的。但柏拉图有关芝诺观点的记叙，却被普遍认为是准确的。

在柏拉图的巴门尼德篇中，当芝诺谈到自己的著作（论自然）时，这样说道：“由于青年时的好胜著成此篇，著成后，人即将他窃去，以至我不能决断，是否应当让它问世。 ”芝诺不象他的老师那样企图从正面去证明是一不是多，是静不是动，他常常从反面即归谬法来为“存在论”辩护。公元五世纪的评论家普罗克洛斯（Proclus）说过，芝诺从“ 多”和运动的假设出发，一共推出了40个各不相同的悖论。现存的芝诺悖论至少有8个，其中关于运动的4个悖论最为著名。

芝诺的著作早已失传，亚里士多德的物理学和辛普里西奥斯为物理学作的注解是了解芝诺悖论的主要途径，此外只有少量零散的文献可作参考。直到19世纪中叶，亚里士多德关于芝诺悖论的引述及批评几乎是权威的，人们普遍认为芝诺悖论不过是一些诡辩。英国数学家B．罗素感慨的说：“在这个变化无常的世界上，没有什么比死后的声誉更变化无常了。死后得不到应有的评价的最典型例子莫过于埃利亚的芝诺了。他虽然发明了四个无限微妙无限深邃的悖论，后世的大批哲学家们却宣称他只不过是个聪明的骗子，而他的悖论只不过是一些诡辩。遭到两千多年的连续驳斥之后这些诡辩才得以正名，…。”

19世纪下半叶以来，学者们开始重新研究芝诺。他们推测芝诺的理论在古代就没能得到完整的、正确的报道，而是被诡辩家们用来倡导怀疑主义和否定知识，亚里士多德正是按照被诡辩家们歪曲过的形象来引述芝诺悖论的。学者们对芝诺提出这些悖论的目的还不清楚，但大家一致认为，芝诺关于运动的悖论不是简单的否认运动，这些悖论后面有着更深的内涵。亚里士多德的著作保存了芝诺悖论的大意，从这个意义上来说，他功不可没，但他对芝诺悖论的分析和批评是否成功，还不可以下定论。

有关芝诺悖论在古希腊数学发展中起到的作用，在科学史上众说纷纭。P·汤纳利首先提出，不是巴门尼德而是毕达哥拉斯学派发现的不可公约量，对芝诺悖论的提出产生了深刻的影响。H·赫斯和H·斯科尔斯则认为芝诺是对古代数学的发展起决定影响的人物，他们试图证明，毕达哥拉斯学派曾假定存在无限小的基本线段，想以此来克服因发现不可公约量而引起的矛盾，而芝诺的悖论反对了这种不准确的做法，从而迫使其他数学家去寻找真正的原因所在。另有一些学者持有完全不同的观点，他们认为芝诺对那个时代的数学发展没有作出任何重大的贡献。

不管争论的结果如何，人们无须担心芝诺的名字会从数学史上消失，就像美国数学史家E·T·贝尔说的，芝诺毕竟曾“以非数学的语言，记录下了最早同连续性和无限性格斗的人们所遭遇到的困难。”芝诺的功绩在于把动和静的关系、无限和有限的关系、连续和离散的关系惹人注意地摆了出来，并进行了辨证的考察。在哲学上，芝诺被亚里士多德誉为辩证法的发明人，黑格尔在他的哲学史演录中指出：“芝诺主要是客观的辨证的考察了运动，并称芝诺为‘辩证法的创始人’”。