3.5 嵌套循环解百钱百鸡问题
3.5.1 循环的嵌套
在循环语句中使用另一个循环语句称为循环的嵌套,也称多重循环。For循环、Do循环和While循环都可以互相嵌套,利用循环的嵌套可以实现更复杂的程序设计。两个For语句嵌套的形式:

例如:
For i = 1 To 3
For j = 1 To 3
Print i, j
Next
Next
执行过程:
i=1 j=1 输出1,1
j=2 输出1,2
j=3 输出1,3 (内层循环完毕,进行外层的下一次循环)
i=2 j=1 输出2,1
j=2 输出2,2
j=2 输出2,2
i=3 j=1 输出3,1
j=2 输出3,2
j=3 输出3,3
不论何种嵌套,外循环都要完整地包含内循环,不允许交叉。程序代码需要有良好的注释和排版风格,否则嵌套的循环语句往往会引起一些程序理解上的混乱。
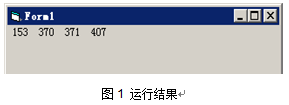
【例1】用三重循环求解水仙花数,“水仙花数”是一个三位数,例如153=13+53+33。
Dim i %, j%, k%
For i = 1 To 9
For j = 0 To 9
For k = 0 To 9
Ifi*100+10*j+ k=i^3+j^3+k^3 Then
Print i*100*10*j+ k
End If
Next k
Next j
Next i
程序运行结果如图1所示。
3.5.2 百钱百鸡问题
百元买百鸡问题:今有鸡翁一,值钱伍;鸡母一,值钱三;鸡雏三,值钱一。凡百钱买百鸡,问鸡翁、母、雏各几何?
答曰:鸡翁四,值钱二十;鸡母十八,值钱五十四;鸡鶵七十八,值钱二十六。又答:鸡翁八,值钱四十;鸡母十一,值钱三十三,鸡鶵八十一,值钱二十七。又答:鸡翁十二,值钱六十;鸡母四、值钱十二;鸡鶵八十 四,值钱二十八。”
“百鸡问题”是中古时期,关于不定方程整数的典型问题,邱建对此有精湛和独到的见解。
【例2】百元买百鸡问题求解,已知鸡翁5元一只,母鸡3元一只,小鸡1元三只,现用100元买100只鸡,求能买鸡翁、母鸡、小鸡各多少只?
算法设计:此题宜采用“穷举法”求解,即对所有可能解,逐个进行试验,若满足条件,就得到一组解,否则继续测试,直到循环结束为止。
求解过程如下:
①假设公鸡母鸡小鸡分别为A,B,C。
②满足的条件:
A+B+C=100
A*5+B*3+C/3=100
③确定取值范围:
A:1~20 B:1~33 C:1~100
编写程序代码如下:
For a=1 to 20
For b=1 to 33
For c=1 to 100
if a+b+c=100 and a*5+b*3+c/3=100 then
Print a,b,c
end if
Next c
Next b
Next a
简化后的代码如下:
For a=1 to 20
For b=1 to 33
c=100-a-b
if a*5+b*3+c/3=100 then
Print a,b,c
end if
Next a,b
程序运行时i、j、k的值分别按下列顺序测试:
i j k
1 1 98
1 2 97
….
1 33 66
2 1 97
2 2 96
….
20 33 47
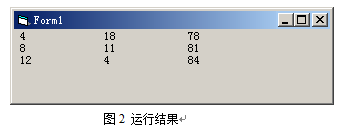
程序运行结果如图2所示,共有三组满足条件的值。
======================================================================================
=====================================================================================


