3.1 程序结构与算法

 3.1.1 算法的概念

 “算法”即演算法的大陆中文名称出自《周髀算经》；而英文名称Algorithm来自于9世纪波斯数学家al-Khwarizmi，因为al-Khwarizmi在数学上提出了算法这个概念。“算法”原为"algorism"，意思是阿拉伯数字的运算法则，在18世纪演变为"algorithm"。欧几里得算法被人们认为是史上第一个算法。

电子计算机的出现，开创了算法研究的新时代。人们可以将算法编写成程序提交给计算机执行．从而迅速获得解题结果。著名计算机科学家高纳德(D．E．Knuth)认为：计算机科学是算法的科学。程序按照算法运行，程序是算法的实现。

事实上，在日常生活中解决问题经常要用算法，只是通常不用算法这个词罢了。例如，乐谱是乐队指挥和演奏的算法；菜谱是厨师做菜的算法等等。在漫长的岁月中，人们发现了很多算法。例如，欧几里得提出的求两个自然数的最大公约数算法，早期希腊学者埃拉多塞尼(Eratosthenes)发现的寻找素数的筛法等都是著名的算法例子。

算法是指对问题求解方法准确而完整的描述，是为解决一个特定问题所采取的确定的有限长的操作序列。算法与数据结构之间存在密切联系。数据结构是算法的基础。数据结构不同，通常采用的算法也会不同，合适的数据结构能够简化算法。算法的设计取决于数据（逻辑）结构，而算法的实现依赖于采用的存储结构。

算法与程序不同，程序是算法的一种描述，同一个算法可以用不同的编程语言来编写，编写程序时要考虑计算机系统运行环境等细节问题，但设计算法可以摆脱这些束缚。算法的基本特征：

（1）有穷性：算法必须在合理的有限时间内，执行有限次数后结束。一个算法必须在有限的操作步骤内以及合理的时间内执行完成。对于一个算法，要求其在时间和空间上均是有穷的。

例如，求解数学中的无穷级数，在实际计算时，必须根据计算的精度要求，确定有限项的累加求和才可能是有穷的算法。除了步骤上的有穷性以外，往往还要求算法执行的时间应该合理。如果让计算机执行一个100年才结束的算法，这虽然是有穷的，但超过了合理的时间范围，就把它视为无效算法。

（2）确定性：算法中的每一个步骤都应当是确定的，而不应当是含糊的、模棱两可的，使算法的执行者或阅读者都能够明确其含义及如何执行，并且在任何条件下，算法都只有一条执行路径。算法中每一条指令的执行必须有唯一的结果，不允许有二义性，即对于相同的输入只能得出相同的输出。”

例如，“赋值为大于0的整数”，这是不确定的，因为大于0的整数有无穷多个。

（3）可行性：算法中描述的操作可以通过已经实现的基本运算有限次地执行来完成。可行性指的是，序列中的每个操作都是可以简单完成的，其本身不存在算法问题，例如，“求x和y的公因子”就不够基本。

（4）输入与输出：输入值即为算法的操作对象，输出是一组与“输入”有确定关系的量值，是算法进行信息加工后得到的结果。一个算法应该有0个或多个输入数据、有1个或多个输出数据。也就是说，算法执行完毕必须有一个或若干个输出，没有输出的算法是毫无意义的。

3.1.2 算法的控制结构

各种运算和操作之间的执行顺序称为算法的控制结构。算法的基本控制结构有三种：顺序、选择、循环。通常用流程图、N-S结构化流程图、算法描述语言等来描述算法。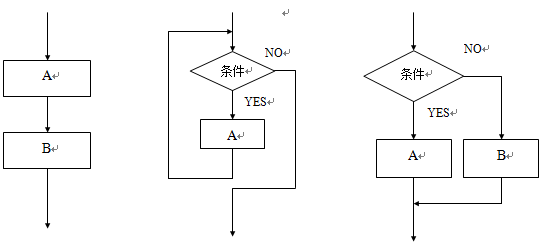

3.1.3 算法的策略

1.穷举法

穷举法：根据题目的条件确定答案的大致范围，并在此范围内对所有可能的情况逐一验证。若某个情况验证符合题目的条件，则为本问题的一个解；若全部情况验证后都不符合题目的全部条件，则本题无解。

例：穷举法求解水仙花数。

2.递推法

递推法是利用问题的递推关系求解的一种方法。设要求问题规模为N的解，当N=1时，解为已知或能非常方便地得到解。递推性质，即当得到问题规模为N=1的解后，问题规模为2，3…，N-1的一系列解可通过递推关系求得。直至得到规模为N的解。

例：递推法求阶乘。

3.递归法 

一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法。它通常把复杂的问题层层转化为与原问题相似的规模较小的问题来求解。在计算机编写程序中，递归算法对解决某一类问题是十分有效的，它往往使算法的描述简洁而且易于理解。

例：递归法求解汉诺塔。

=========================================================================================

========================================================================================