公元前1550年，巴比伦人已经知道如何解二元一次方程组了^[1]，公元前200年，《九章算术》第8章的多个问题展示了解线性方程组的能力。不同于千年后的高斯消元法，这些方法只处理系数，思维方式上更接近矩阵运算。

现代线性代数源于微积分创始人莱布尼茨（Leibnitz）对求解线性方程组的研究。1693年，他发明了行列式。

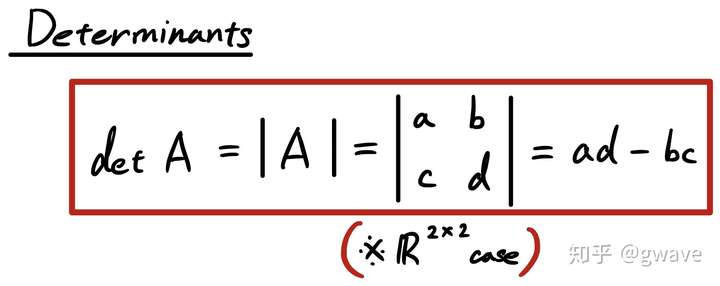
可以把行列式看成一个函数，输入一个方阵，输出一个数值（标量）。拉格朗日发现行列式的体积性质：2阶行列式对应2个向量围成的平行四边形面积，3阶行列式对应平行六面体的体积，更高阶的无法可视化，请各位自行脑补。

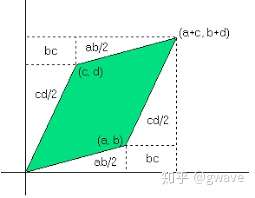
行列式如果等于0，意味着向量之间存在线性依赖，也就是共线了，面积/体积为0，矩阵不可逆， 对应的方程组无解（非齐次，等号右边不等于0）或有无数解（齐次，等号右边等于0）。

1750年，克莱默（Gabriel Cramer）提出了基于行列式的（但没有给出证明） $n\times n$ 方程组的解法，即克莱默法则。实际中没有人会用克莱默法则求解线性方程组，会累死你，高斯消元法总是更有效。国内教科书大多从行列式开始，让人对线代第一印象就是繁复而难以下咽。

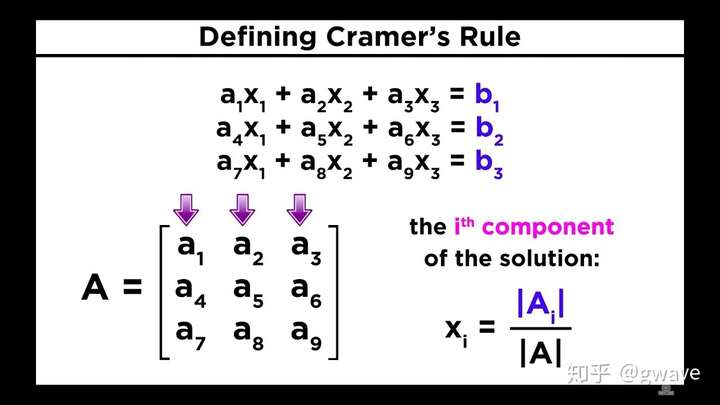
同样在1750年，欧拉注意到了一个方程可能被另一个方程所“包含”^[2]，他以3x − 2y = 5 和 4y = 6x − 10为例，质疑 $n\times n$ 的方程组一定存在唯一解，他称之为“包含性依赖”（inclusive dependence），今天我们称之为“线性依赖”，对应于克莱默法则中分母为0的情况。欧拉和克莱默的工作与前人不同，矩阵的雏形从线性方程组求解中逐渐脱胎出来，具有了自己的性质，但还没有自己的名字。

总的来说，18世纪的相关研究主要围绕着行列式进行，研究对象是方阵 —— $n$ 个方程对应 $n$ 个未知变量的情况，主要目的是解线性方程组。

1801年，高斯在预测谷神星轨道时发明了最小二乘法，也引入了高斯消元法，这是种系统性的线性方程组解法，他在对天体轨道建模时处理了12个方程对应6个未知变量的“超定”情况。他已经清楚地了解方程组有多个解，1个解还是无解的条件，但他还没有使用矩阵表达方程组。

1850年，英国数学家 James Joseph Sylvester (1814-1897) 将“矩阵”（Matrix）作为术语提出，Matrix源于拉丁语“子宫”(womb之意)，他认为矩阵是行列式之母，行列式是矩阵之子，2000年的大片《MATRIX》将Matrix译为“母体”其实不无道理。从历史的出现顺序来看，先有行列式再有矩阵，可见，先有支付宝再有蚂蚁金服也合理。

今天的线代书籍第一章如果还是行列式，虽然与历史发展顺序保持一致，但却不是学习矩阵的最优顺序。行列式在特征值/向量章节中作为一节出现较合适。

1855年，Sylvester和他一生的挚友Arthur Cayley (1821-1895)发表文章，首次以矩阵的形式表达线性方程组。一种强大的新的数学语言从此诞生！拉普拉斯说：简化的记法常常是深奥理论的源泉，举个略夸张的例子：有人说莱布尼茨的微分表示法 $\frac{dy}{dx}$ 使欧洲微积分领先使用牛顿记法 $\dot{x}$的英国100年。深度学习本质上特征学习，也是对数据特征进行了更好的表达。可见，良好的的表达形式非常重要！

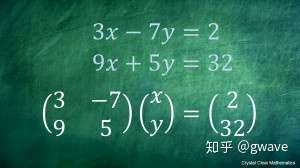
Cayley是第一个把矩阵作为独立的对象进行研究的人。1858年，他发表了矩阵领域里程碑文章 Memoir on the Theory of Matrices，定义了今天行列式的表示法、矩阵加法、数乘、乘法、次方、单位矩阵、零矩阵和逆矩阵，Cayley-Hamilton定理达到了顶峰，他被公认为矩阵的创立者。Cayley是一位高产数学家，与他在群论、图论和不变量理论方面的贡献相比，线代方面的贡献被掩盖了，而且，很多工作是在十几年律师生涯中利用业余时间做的。

柯西（Augustin-Louis Cauchy， 1789-1857）引入了特征值和特征分解，矩阵的对角化和相似矩阵等概念，他称特征值（Eigenvalue）为 Characteristic root。

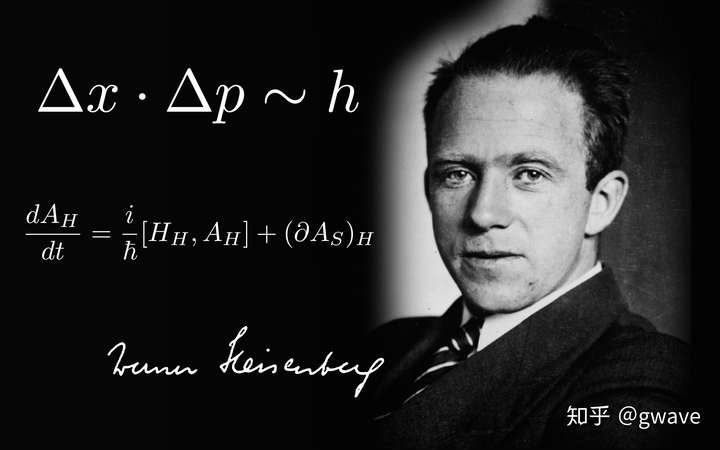
进入20世纪，矩阵被被广泛应用于不同领域：海森堡在量子力学中，冯诺伊曼在计算机中都开始应用了矩阵，纳什在博弈论中……。

今天，机器学习更是将矩阵作为最基础的工具，矩阵运算已经成为大数据时代的加减乘除，在从现实的原子世界向虚拟的比特世界迁移中，矩阵像阳光和氧气一样无所不在。

参考

1. ^https://tojsat.net/journals/tojsat/articles/v07i01/v07i01-12.pdf

2. ^https://iola.math.vt.edu/media/pubs/Andrews-Larson_2015.pdf