线性代数序言

为什么要学习线性代数

首先找一下线性代数在整个数学系列中的位置。

“为什么学习线性代数？线性代数到底在讲什么？”刚接触这门学科的同学可能都会提类似的问题。

  简短的回答就是：

        （1）我们所处的世界、宇宙太复杂了，很多现象都无法理解，更谈不上用数学去描述；

        （2）有一些符合特定条件的复杂问题，可以转化为简单的线性问题，线性问题就完全可以理解，  完全可以被数学所描述（怎么把复杂问题转为线性问题是别的学科要解决的，比如说微积分）；

        （3）线性代数就是研究怎么解决线性问题的。

举两个例子，展示下我们所处的世界、宇宙到底有多复杂。

1 三体

科幻小说《三体》描述了一个三体世界，这是一个周围有三个“太阳”的行星（这样的行星在宇宙中是有原形的）：

在引力的作用下，三个“太阳”互相推拉，导致它们的运行轨迹十分复杂，这样的问题可以称为“三体问题”。                      其中的行星（下图中最小的球体），也就是三体世界被牵扯着四处运动：

这样导致的结果是，三体世界上的环境非常恶劣：如果三个“太阳”同时靠近它，那么温度就会非常高；三个“太阳”同时远离，则又变成冰封大陆；只有在三个“太阳”不远不近、不多不少的靠近它时，会有那么一段适合生物发展的时期。

在这样残酷的环境中，反复地毁灭和创造下，孕育出了比人类先进很多的三体文明。就是这样的先进文明也没有办法预测三个“太阳”的轨迹。有可能短暂地预测成功了，但是偶尔路过的彗星，或者远处的超新星爆炸等，又会给非常不稳定的三体系统带来搅动，导致运动轨迹重新变得扑朔迷离。

2 散热

三体的例子很遥远，下面来看一个生活中的例子。下面是电脑里面的显卡，左侧是显卡风扇。从动图中可

以看出，工作中的显卡有的地方温度很高，风扇吹出来的风不断在给显卡降温：

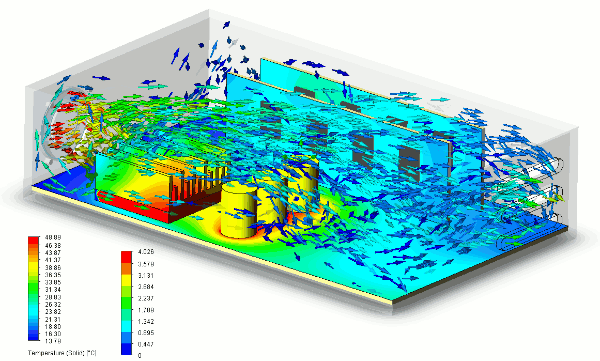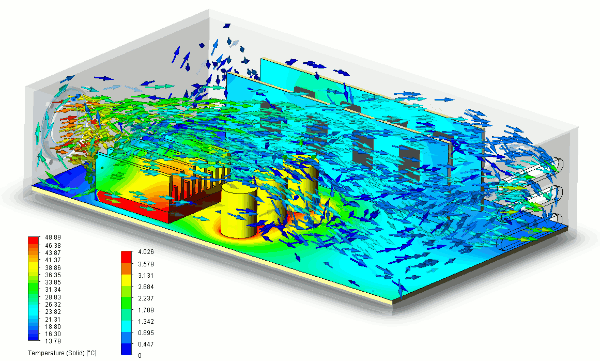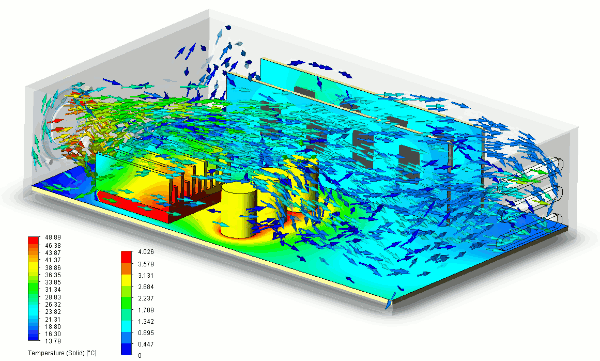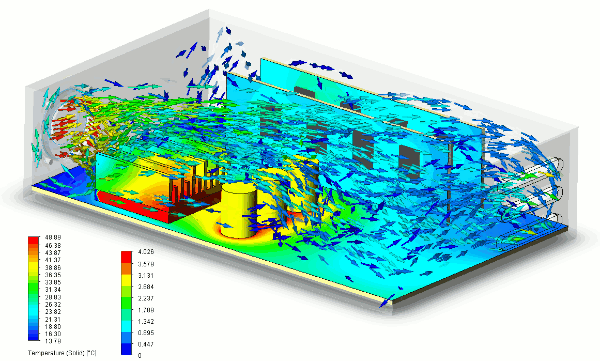
由于各种器件的存在，以及气流的相互影响，导致风的运动非常复杂。假如要去计算某一时刻、某一点的风力大小和方向，可想而知难度会有多大。

相对于复杂的世界而言，线性问题是非常简单的。下面笼统说下什么是线性问题。

1 线性

有一类几何对象，比如直线、平面、立方体，看上去都是有棱有角的，都是“直”的，在数学中称为“线性”

（本课程后面会给出线性的严格定义，现在先这么称呼吧）：

2 线性问题

要处理它们，以及和它们相关的问题就非常简单。比如在高中就学过，两根直线可以用两个线性方程来表示，想求它们交点的话：

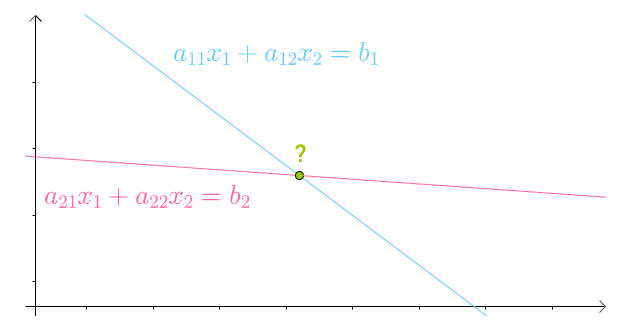
联立出两者的方程组，求出该方程组的解就可以得到交点：

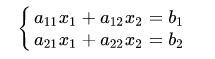
这里举的例子很简单，随着后面的深入学习就会知道，线性问题还是有一定的复杂性，不然不会需要《线性代数》这门学科来研究线性问题。

复杂的世界介绍了，简单的线性问题也介绍了，之前说了，某些复杂问题可以转为简单的线性问题，或者称为复杂问题可以，下面就来看几个例子。

1 静态

不规则曲线挺复杂的，不过在一定的条件下，点附近的曲线可以用一根直线来代替（这是《单变量微积分》中的内容）：

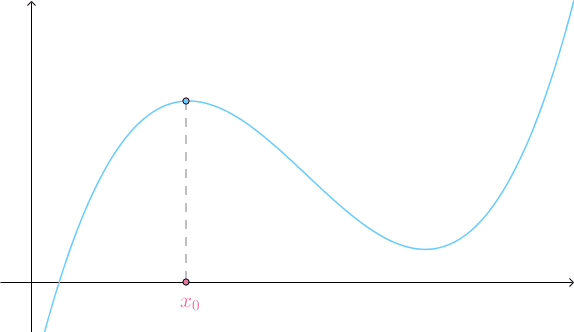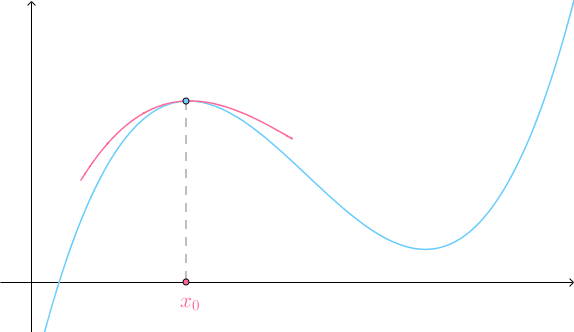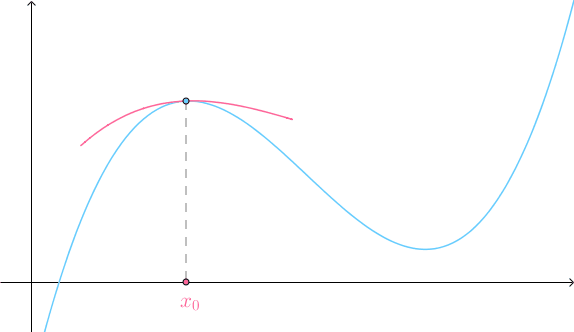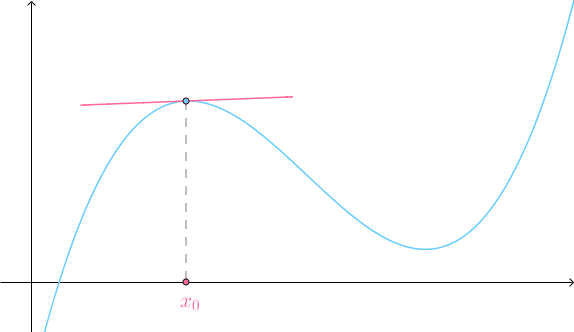
不规则曲面也蛮复杂的，也是在一定的条件下，空间内一点附近的曲面可以用一个平面来代替（这是《多变量微积分》中的内容）：

2 动态

在5G通信中，会遇到各种各样复杂的周期波，我们可以通过正弦函数来近似这些周期波（这是《信号与系统》中的内容）：

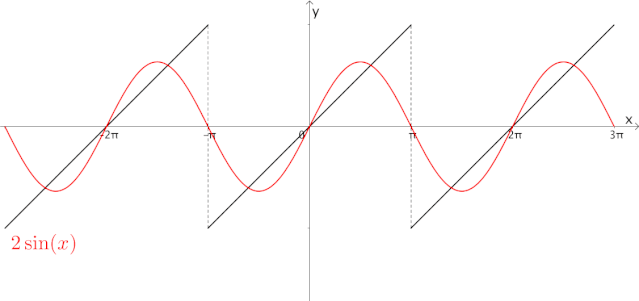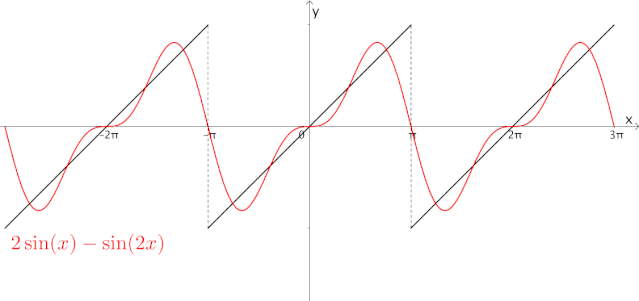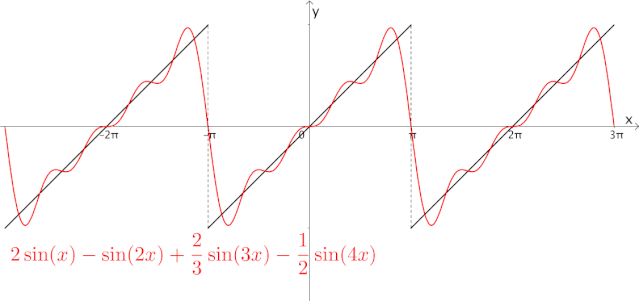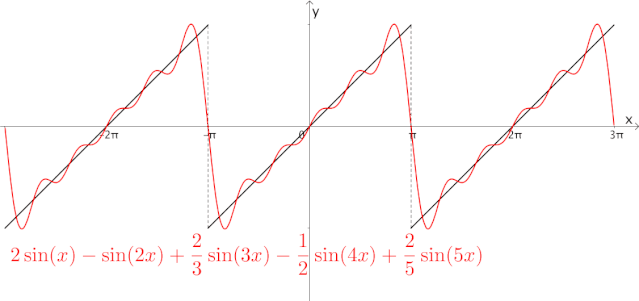
为什么要用正弦函数来近似？这是因为，如果将一根线段旋转一圈，记录该线段在Y轴上的轨迹，得到的就是正弦函数：

也就是说，正弦函数实际上是运动的线段，也是线性的。那么用正弦函数来近似周期波，就相当于将各种复杂的周期波的问题给线性化了。

人脸识别

之前的例子比较直觉，下面通过人脸识别给出一个具体的例子，虽然相对于真正的应用而言，这个例子已经极度简化了，大家还是可以看到是怎么通过线性化来解决像人脸识别这样的复杂问题的。

下图中，有两张照片是同一个人的：

对于这个问题，人是很容易分辨出来的，但计算机应该怎么办呢？其中一种方法就是将之线性化。首先，给出此人更多的照片：

将其中某张照片分为眼、鼻、嘴三个部位，这是人脸最重要的三个部位。通过某种算法，可以用三个实数来分别表示这三个部位，比如下图得到的分别是150、30、20：

将所有这些照片分别算出来，用三维坐标来表示得到的结果，比如上图得到的结果就是（150,30,20）。将这些三维坐标用点标注在直角坐标系中，发现这些点都落在某平面上，或该平面的附近。因此，可认为此人的脸线性化为了该平面（学习了《概率与统计》才有能力构建出这个平面）：

将人脸线性化为平面后，再给出一张新的照片，按照刚才的方法算出这张照片的三维坐标，发现不在平面上或者平面附近，就可以判断不是此人的照片：

总结下，人脸识别就是把之前的人脸线性化为平面，然后判断新的照片是否在该平面内：

这里面有两个数学问题：

        （1）怎么表示人脸线性化后的平面？

        （2）怎么判断人脸是否在该平面内？

线性代数提供了这两个数学问题的解决方案。

1 向量和向量空间

第一个问题，怎么表示人脸线性化后的平面？线性代数提供了向量或向量空间来表示平面、直线以及立体等线性的几何对象：

2 矩阵函数

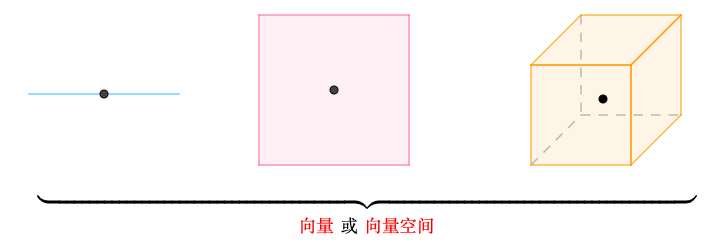
第二个问题，怎么判断人脸是否在该平面内？线性代数提供了关于向量和向量空间的函数，也就矩阵函数，或者简称为矩阵。这样可以很方便的判断出新的照片是否在之前线性化得到的平面上（下面的不等于就表示不在平面上）：

线性代数

综上，线性代数要学习的内容就是如何解决线性问题（再重复一下，如何把复杂问题线性化是别的学科的内容，比如《微积分》、《信号与系统》、《概率与统计》等），下面的内容就是本课程会讨论的线性问题：

• 什么是向量、向量空间

• 关于向量、向量空间的函数，也称为矩阵函数

• 对矩阵函数进行坐标变换（之前没有提到这点，但是对于复杂的线性问题，需要进行坐标变换）

掌握了以上内容，才具备了处理复杂问题的部分基础能力，因此线性代数是工科、理科的必修科目。

接下来的学习中会对这些内容进行详细介绍，最后也会回答之前提到的人脸识别中的与线性代数相关的细节，让我们带着好奇心前行吧。