【多维随机变量及其分布】

多维随机变量产生的原因：随机试验结果有时需要同时用两个甚至更多个量来描述。

例如：描述学生的成绩，包含多门不同课的成绩，每门课的成绩都是一个随机变量。

【联合分布函数】

联合分布函数的性质

q F(x,y)是x,y的非减函数；

q 0 ≤ F(x,y) ≤ 1

     q  F(﹣∞,y) =F(x,﹣∞)=F(﹣∞,﹣∞)=0

       q  F(﹣∞,﹣∞)=1

q F(x,y)关于x,y右连续；

q 对任意(,)和(,)，且＜，＜，则有：

         

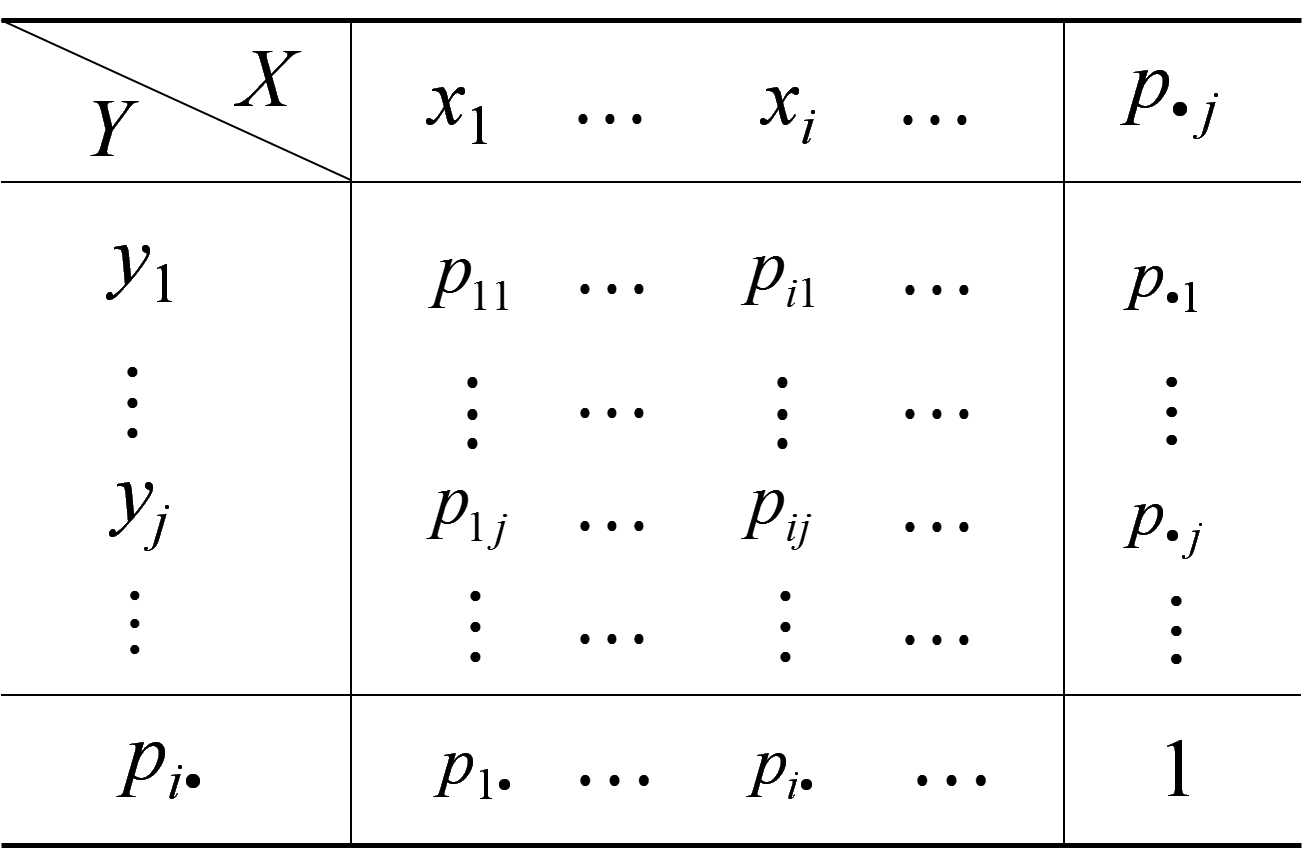
【离散型随机变量的联合分布律】

联合分布律及边缘分布律