史瓦西黑洞是1916年由史瓦西（Schwarzschild）提出来的， 史瓦西黑洞的设定是不带电不自旋转的黑洞，黑洞中心为奇点， 黑洞的外圈为事件视界，又称史瓦西半径。时空里可能发生的事件到了事件视界上， 就好像面临了穹端极界，停滞不变了，对外部的观察者看来，时间好像停止不动了。 对于一个静止不带电的史瓦西黑洞， 它的周围时空可以利用史瓦西度规描述史瓦西黑洞的区间微分平方。 利用其可算出史瓦西黑洞的半径即事件穹界的大小为r = 2MG / c^2 。

史瓦西半径是任何具重力的质量之临界半径。在物理学和天文学中，尤其在万有引力理论、广义相对论中它是一个非常重要的概念。1916年卡尔·史瓦西首次发现了史瓦西半径的存在，他发现这个半径是一个球状对称、不自转的物体的重力场的精确解。一个物体的史瓦西半径与其质量成正比。太阳的史瓦西半径约为3千米，地球的史瓦西半径只有约9毫米。小于其史瓦西半径的物体被称为黑洞。在不自转的黑洞上，史瓦西半径所形成的球面组成一个视界。（自转的黑洞的情况稍许不同。）光和粒子均无法逃离这个球面。银河中心的超大质量黑洞的史瓦西半径约为780万千米。一个平均密度等于临界密度的球体的史瓦西半径等于我们的可观察宇宙的半径。

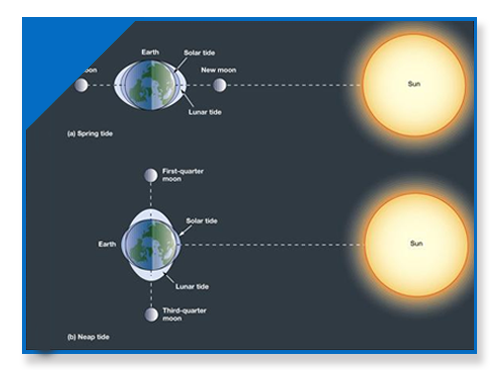
在理论推理和数理分析的基础上，获得了地球产生周期性涨落变形的潮汐力表达式，由潮汐力导致的潮汐，其波长和振幅随地球离黄道面的远近不同而变化，随着距离增加，波长与振幅逐渐减小，但同一环线上振幅各点一致，周期约12h地球的胀缩特性和沿轨道径向的变化速度，是影响地球潮汐能量的决定因素之一，地球公转轨道的 2 68°1 5′处为潮汐能量最大处。地球的潮汐力是由椭圆轨道运动产生的，由于月球的轨道运动是以地球为焦点，所以在月球上可以产生受地球影响的潮汐，而不可以产生相反的潮汐，因为海水或岩浆没有以月球为焦点的轨道运动 。

当引力源对物体产生力的作用时，由于物体上各点到引力源距离不等 所以受到引力大小不同 从而产生引力差，对物体产生撕扯效果，这种引力差就是潮汐力。