生物统计学复习题

一、名词解释

1.个体:个体是组成总体的基本单元。

2.变量:变量是相同性质的事物间表现差异性的某种特征。

3.参数:参数是描述总体特征的数量。

4.统计数:统计数是描述样本特征的数量。

5.因素:因素是指试验中所研究的影响试验指标的原因或原因组合。

6.总体:统计总体简称总体是我们要调查或统计某一现象全部数据的集合。

7.变异系数:标准差与平均数的比值称为变异系数，记为C.V。变异系数可以消除单位和（或）平均数不同对两个或多个资料变异程度比较的影响。

8.样本:研究中实际观测或调查的一部分个体称为样本。

9.样本容量:又称“样本大小”,在一个样本中所包含的个案或单元数。

10. 简单随机抽样法:又称纯随机抽样，它是按随机原则直接从总体N个单位中抽取n个单位作样本，这种抽样方式能使总体中每一个单位有同等机会被抽中，这种方式是抽样中最基本的，也是最简单的方式。

11.中心极限定理：如果被抽样总体不是正态总体，单具有平均数μ和方差σ2，当随样本容量n的不断增大，样本平均数的分布也越来越接近正态分布，且具有平均数μ和σ2方差。

12.互作：某一因素在另一因素的不同水平上所产生的效应不同，则两因素间存在交互作用，简称互作。

13.多重比较：明确不同处理平均数两两间差异的显著性，每个处理的平均数都要与其他的处理相比较，这种差异显著性检验叫多重比较。

14.决定系数：相关系数r的平方，其含义是变量x引起y变异的回归平方和占y变异总平方和的比率，用于表示两个变量间的相关程度。

15.因素水平：对试验因素所设定的量的不同级别或质的不同状态称为因素的水平（factorlevel），简称水平。

16.试验单位：亦称试验单元（experimentalunit），是指施加试验处理的材料单位。这个单位可以是一个小区，也可以是一穴、一株、一穗、一个器官等。

17.观测值：对样本中各个体的某种性状、特性加以考察，如称量、度量、计数或分析化验所得的结果称为观测值。

二、填空题

1.相关系数的取值范围为（[一1，1]）。

2.用来说明回归方程代表性大小的统计分析指标是（F）。

3.统计上常用（回归）分析来研究呈因果关系的两个变量间的关系，用（相关）分析来研究呈平行关系的两个变量间的关系。

4.对于简单直线回归方程，其回归平方和的自由度为（1）。

5.在直线回归方程中，当自变量改变一个单位时，依变量平均增加或减少的单位数可用（b或回归系数）来表示。

6.统计推断主要包括（假设检验）和（参数估计）两个方面。

7.参数估计包括（点）估计和（区间）估计。

8.假设检验首先要对总体提出假设，一般应作两个假设，一个是（无效假设／零假设／H0），另一个是（备择假设／H1）。

9.对一个大样本的平均数来说，一般将接受区和否定区的两个临界值写成（）。

10.在频率的假设检验中，当np或nq（<）30时，需进行连续性矫正。

11.卡平方测验的连续性矫正的前提条件是自由度等于（1）。

12.从总体中抽取的样本要具有代表性，必须是（随机）抽取的样本。

13.从一个正态总体中随机抽取的样本平均数，理论上服从（正态分布）。

14.在一定的概率保证下，估计参数可能出现的范围和区间，称为（置信区间 / 置信阈）。

15.试验误差分为（系统误差）和（随机误差）。

16.在拟定试验方案时，必须在所比较的处理之间应用（唯一差异）的原则。

17.在多重比较中，当样本数大于等于3时，t测验，SSR测验、q测验的显著尺度，（q测验）最高，（t测验）最低。

18.试验资料按所研究的性状、特性可以分为（数量性状）和（质量性状）资料。

19.样本可根据样本容量的多少为：（大样本）和（小样本）。

20.对比法、间比法试验，由于处理是作（顺序）排列，因而不能够无偏估计出试验的误差。

21.小区的形状有（长方形）、（正方形）。一般采用（长方形）小区。

22.在边际效应受重视的试验中，方形小区是有利的，因为就一定的小区面积来讲，方形小区具有最小的（周长），使受到影响的植株最少。

23.完全随机设计应用了试验设计的（重复）和（随机）两个原则。

24.试验设计的三个基本原则是（重复）、（随机）和局部控制。

25.在田间试验中，设置区组的主要作用是进行（局部控制）。

26.试验方案试验计时，一般要遵循以下原则：（明确的目的性）、（严密的可比性）和（试验的高效性）。

27.试验误差分为（随机误差）和（系统误差），一般所指的试验误差为（随机误差）。

三、判断题

1.计数资料也称为连续性变量资料，计量资料也称为非连续性变量资料。（ ×   ）

2.抽样误差是抽样调查中无法避免的误差。（  √  ）

3.抽样误差的产生是由于破坏了随机原则所造成的。（  ×  ）

4.在进行抽样调查时，样本容量越大，其抽样误差也越大。（  ×  ）

5.顺序抽样可以计算其抽样误差。（  ×  ）

6.简单随机抽样适用于个体间差异较小、所需抽取的样本单位数较小的情况。（  √  ）

7.回归系数b的符号与相关系数r的符号，可以相同也可以不同。（  ×  ）

8.回归分析和相关分析一样，所分析的两个变量都一定是随机变量。（ ×   ）

9.在直线回归分析中，两个变量是对等的，不需要区分因变量和自变量。（  ×  ）

10.正相关指的就是两个变量之间的变动方向都是上升的。（  ×  ）

11.对于有限总体不必用统计推断方法。（  ×  ）

12.资料的精确性高，其准确性也一定高。（  ×  ）

13.在试验设计中，随机误差只能减小，而不可能完全消除。（  √  ）

14.统计学上的试验误差，通常是指随机误差。（  √  ）

15.当直线相关系数r=0时，说明变量之间不存在任何相关关系。（  ×  ）

16.如果两个变量的变动方向一致，同时呈上升或下降趋势，则二者是正相关关系。（ √ ）

17.作假设检验时，如果|μ|>μα，应接受H0，否定H1。（ ×  ）

18.作单尾检验时，查μ或t分布表(双尾)时，需将双尾概率乘以2再查表。（√  ）

19.第一类错误和第二类错误的区别是：第一类错误只有在接受H0时才会发生；第二类错误只有在否定H0时才会发生。（  ×  ）

20. χ2检验只适用于离散型资料的假设检验。（  ×  ）

21.多数的系统误差是特定原因引起的，所以较难控制。（  ×  ）

22.否定正确无效假设的错误为统计假设测验的第一类错误。（√  ）

23.A群体标准差为5，B群体的标准差为12，B群体的变异一定大于A群体。（  ×  ）

24.“唯一差异”是指仅允许处理不同，其它非处理因素都应保持不变。（√   ）

25.由固定模型中所得的结论仅在于推断关于特定的处理，而随机模型中试验结论则将用于推断处理的总体。（√  ）

26.对频率百分数资料进行方差分析前，应该对资料数据作反正弦转换。（  ×  ）

27.多重比较前，应该先作F测验。（  ×  ）

28.有一直线相关资料计算相关系数r为0.7，则表明变数x和y的总变异中可以线性关系说明的部分占70％。（  ×  ）

29.生物统计方法常用的平均数有三种：算术平均数、加权平均数和等级差法平均数。（  ×  ）

四、单项选择题

1.事先将全部总体各单位按某一标志排列，然后依固定顺序和间隔来抽选调查单位的抽样方式为（ D  ）。

   A．分层随机抽样  B．简单随机抽样  C．整群抽样  D．顺序抽样

2. 关于平均数，下列说法正确的是（  B  ）。

   A．正态分布的算术平均数与几何平均数相等

   B．正态分布的算术平均数与中位数相等

   C．正态分布的中位数与几何平均数相等

   D．正态分布的算术平均数、中位数、几何平均数均相等

3.如果对各观测值加上一个常数c，其标准差（  D  ）。

          A．扩大        B．扩大c倍      C．扩大倍     D．不变

4. 关于泊松分布参数λ错误的说法是（  C  ）。

   A．μ=λ  B．σ2=λ   C．σ=λ    D．λ=np

5. 正态分布曲线由参数μ和σ决定，μ值相同时，σ取（  D  ）时正态曲线展开程度最大，曲线最矮宽。

   A．0.5   B．1   C．2    D．3

6. 当样本容量n<30且总体方差σ2未知时，平均数的检验方法是（  A  ）。

   A．t检验    B．μ检验    C．F检验   D．χ2检验

7. 两样本方差的同质性检验用（  B  ）

   A．μ检验    B．F检验    C．t检验D．χ2检验

8. 已知某批25个小麦样本的平均蛋白质含量和σ，则其在95％置信度下的蛋白质含量的区间估计L（D）。

    A． B.   C.   D.

9. χ2检验时，如果实得，即表明(  C  )。

   A．P<α,应接受H0,否定H1   B．P>α,应接受H0,否定H1

   C．P<α,应否定H0,接受H1   D．P>α,应否定H0,接受H1

10. 在单因素方差分析中，表示(  A  )。

           A．组内平方和    B．组间平方和    C．总平方和    D．总方差

11. 在回归直线中，b<0，则x与y之间的相关系数(  D  )。

           A．r=O   B．r=1   C．O<r<1    D．一1<r<O

12. 由样本求得r=-0.09，同一资料作回归分析时，b值应为(  A  )。

    A．b<O    B．b>O    C．b=O    D．b≥O

13. 对线性回归系数进行t检验时，其自由度为(  A  )。

    A．n-2    B．n-1    C．n  D．2n-1

14. 在直线回归分析中，最小二乘法的本质要求是(  D  )。

   A．各点到直线的垂直距离的和最小

   B．各点到x轴的纵向距离的平方和最小

   C．各点到直线的垂直距离的平方和最小

   D．各点到直线的纵向距离的平方和最小

15. 在线性回归分析中，剩余平方和反映了（  C  ）。

   A．因变量y的变异度    B．自变量x的变异度

   C．扣除x影响后y的变异度    D．扣除y影响后x的变异度

16.在t检验时，如果t=0.01，此差异是（  B  ）

    A.显著水平  B.极显著水平  C.无显著差异   D.没法判断

17.生物统计中t检验常用来检验（  A  ）

    A.两均数差异比较        B.两个数差异比较

    C.两总体差异比较        D.多组数据差异比较

18.平均数是反映数据资料（  B  ）性的代表值。

   A.变异性   B.集中性  C.差异性   D.独立性

19.在假设检验中，是以（  C  ）为前提。

   A.肯定假设 B.备择假设  C.原假设   D.有效假设

20.抽取样本的基本首要原则是（  B  ）

    A.统一性原则  B.随机性原则  C.完全性原则    D.重复性原则

21.下面变量中属于非连续性变量的是（  C  ）。

   A．身高    B．体重    C．血型    D．血压

22.对某鱼塘不同年龄鱼的尾数进行统计分析时，可作成（  A  ）图来表示。

   A．条形图    B．直方图    C．多边形图    D．折线图

23.比较大学生和幼儿园孩子身高的变异度，应采用的指标是（  C  ）。

    A．标准差    B．方差    C．变异系数    D．平均数

24. 一批种蛋的孵化率为80％，同时用两枚种蛋进行孵化，则至少有一枚能

孵化出小鸡的概率为（  A  ）。

    A．0.96    B．0.64    C．0.80    D．0.90

25. 设z服从N(225，25)，现以n=100抽样，其平均数标准误为（  B  ）。

    A．1.5    B．0.5    C．0.25   D．2.25

26. 两样本平均数进行比较时，分别取以下检验水平，以（  A  ）所对应的犯

第二类错误的概率最小。

    A．α=0.20  B． α=0.10    C． α=0.05   D．α=0.01

27．进行平均数的区间估计时，（  B  ）．

    A．n越大，区间越大，估计的精确性越小

    B．n越大，区间越小，估计的精确性越大

    C．σ越大，区间越大，估计的精确性越大

    D．σ越大，区间越小，估计的精确性越大

28. χ2检验中，统计量χ2值的计算公式为（ A ）。

            A.        B．

 

            C．       D.

29.遗传学上常用(  B  )来检验所得的结果是否符合性状分离规律。

    A．独立性检验    B．适合性检验    c．方差分析    D．同质性检验

30.表示（  C  ）。

    A．组内平方和    B．组间平方和    C．总平方和    D．总方差

31.方差分析计算时，可使用（  A  ）种方法对数据进行初步整理。

    A．全部数据均减去一个值

    B．每一处理减去一个值

    C．每一处理减去该处理的平均数

    D．全部数据均除以总平均数

32. 相关分析是研究(  C  )。

    A．变量之间的数量关系

    B．变量之间的变动关系

    C．变量之间的相互关系的密切程度

    D．变量之间的因果关系

33. 在直线相关分析中，当相关系数r=O时，表明（  D  ）。

    A．变量之间完全无关    B．相关程度较小

    C．变量之间完全相关    D．无直线相关关系

34. 若r<rα时，则在α显著水平上可认为相应的两变量x、y间（  D  ）。

    A．不存在任何关系

    B．有直线相关关系

    C．有确定的函数关系

    D．不存在直线相关关系，但不排除存在某种曲线关系

35.如果直线相关系数r=1，则一定有（  C  ）。

    A．SS总=SS残    B．SS残=SS回

    C．SS总=SS回    D．SS总>SS回

36.下列数值属于参数的是（  A  ）

    A.总体平均数   B.自变量

    C.依变量       D.样本平均数

37.下面一组数据中属于计量资料的是（  D  ）

    A.产品合格数    B.抽样的样品数

    C.病人的治愈数  D.产品的合格率

38.在一组数据中，如果一个变数10的离均差是2，那么该组数据的平均数是（  C  ）

   A.12    B.10   C.8     D.2

39.变异系数是衡量样本资料（  A  ）程度的一个统计量。

   A.变异  B.同一  C.集中  D.分布

40.方差分析适合于（  A  ）数据资料的均数假设检验。

    A.两组以上    B.两组    C.一组    D.任何

41.正态分布不具有下列哪种特征（  D  ）。

    A.左右对称  B.单峰分布  C.中间高、两头低  D.概率处处相等

五、简答题

1. χ2检验主要有几种用途?各自用于什么情况下的假设检验?

χ2检验主要有3种用途：样本方差的同质性检验、适合性检验和独立性检验。样本方差的同质性检验用于检验一个样本所属总体方差和给定总体方差是否差异显著；适合性检验是比较观测值与理论值是否符合的假设检验；独立性检验是判断两个或两个以上因素间是否具有关联关系的假设检验。

2. χ2检验的主要步骤有哪些?什么情况下χ2值需要进行连续性矫正?

 (1)提出无效假设H0：观测值与理论值的差异由抽样误差引起，即观测值=理论值；备择假设H1：观测值与理论值的差值不等于0，即观测值≠理论值。

 (2)确定显著水平α。一般可确定为0.05或0.01。

 (3)计算样本的χ2,求得各个理论次数E。并根据各实际次数Oi，代人χ2值公式，计算样本的χ2值。

 适合性检验时，自由度df=k-1(k为分组数)；独立性检验时，自由度为df=(r-1)(c-1)(r为列联表的行数，c为列联表的列数)。

 当自由度df=1时，χ2值需进行连续性矫正：

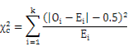
 当自由度df>1时，

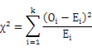
(4)进行统计推断。如果实得，应接受H0，否定H1，说明在α显著水平下观测值与理论值差异不显著，二者间的差异由抽样误差造成；如果实得，应否定H0，接受H1，说明在α显著水平下观测值与理论值差异显著，二者间的差异是真实存在的。

3.什么是方差分析?方差分析的基本思想是什么?进行方差分析一般有哪些步骤?

方差分析的基本思想：将测量数据的总变异按照变异来源分解为处理效应和误差效应，在一定显著水平下进行F检验和多重比较，从而检验处理效应是否显著。

方差分析的基本步骤：①将样本数据的总平方和与总自由度分解为各变异因素的平方和与自由度；②列方差分析表进行F检验，分析各变异因素在总变异中的重要程度；③若F检验显著，对各处理平均数进行多重比较。

4. 什么是多重比较?多重比较有哪些方法?多重比较的结果如何表示?

多个平均数两两间的相互比较称为多重比较。多重比较常用的方法有最小显著差数法(LSD法)和最小显著极差法(LSR法)，其中LSR法又有新复极差法(SSR法)和q法。

       多重比较常以标记字母法和梯形法表示。标记字母法是将全部平均数从大到小依次排列，然后在最大的平均数上标字母a，将该平均数与以下各平均数相比，凡相差不显著的都标上字母a，直至某个与之相差显著的则标以字母b。再以该标有b的平均数为标准，与各个比它大的平均数比较，凡差数不显著的在字母a的右边加标字母b。然后再以标b的最大平均数为标准与以下未曾标有字母的平均数比较，凡差数不显著的继续标以字母b，直至差异显著的平均数标以字母c，再与上面的平均数比较。如此重复进行，直至最小的平均数有了标记字母，并与上面的平均数比较后为止。这样各平均数间，凡有相同标记字母的即为差异不显著，凡有不同标记字母的即为差异显著。差异极显著标记方法

同上，用大写字母标记。

梯形法是将各处理的平均数差数按梯形列于表中，并将这些差数进行比较。差数>LSD(LSR)0.05。说明处理平均数间的差异达到显著水平，在差数的右上角标“*”号；差数>LSD(LSR)0.01，说明处理平均数间差异达到极显著水平，在差数的右上角标“**”号。差数≤LSD(LSR)0.05，说明差异不显著。

5. 方差分析有哪些基本假定?为什么有些数据需经过转换后才能进行方差分析?

方差分析有3个基本假定：正态性(试验误差服从正态分布)、可加性(处理效应与误差效应线性可加)、方差同质性(误差方差具有同质性)。方差分析的有效性是建立在这3个基本假定的基础上的。

在研究中会出现一些样本，其所来自的总体和方差分析的基本假定相抵触，这些数据

在进行方差分析之前必须经过适当的处理，即数据转换来变更测量标尺。

6. 假设检验中的两类错误是什么?如何才能少犯两类错误?

在假设检验中，如果H0是真实的，检验后却否定了它，就犯了第一类错误，即α错误或弃真错误；如果H0不是真实的，检验后却接受了它，就犯了第二类错误，即β错误或纳伪错误。为了减少犯两类错误的概率，要做到以下两点：一是显著水平α的取值不可太高也不可太低，一般取0.05作为小概率比较合适，这样可使犯两类错误的概率都比较小；二是尽量增加样本容量，并选择合理的试验设计和正确的试验技术，以减小标准误，减少两类错误。

7. 什么叫回归分析？回归截距和回归系数的统计学意义是什么？

回归分析是用来研究呈因果关系的相关变量间关系的统计分析方法，其中表示原因的变量为自变量，表示结果的变量为依变量。回归截距是当自变量为零时，依变量的取值，即回归直线在y轴上的截距；回归系数是回归直线的斜率，其含义是白变量改变一个单位，依变量y平均增加或减少的单位数。

8. 什么是统计推断?统计推断有哪两种?其含义各是什么?

统计推断就是根据理论分布由一个样本或一系列样本所得的结果来推断总体特征的过程。统计推断主要包括假设检验和参数估计两个方面。假设检验是根据总体的理论分布和小概率原理，对未知或不完全知道的总体提出两种彼此对立的假设，然后由样本的实际结果，经过一定的计算，作出在一定概率水平(或显著水平)上应该接受或否定的那种假设的推断。参数估计则是由样本结果对总体参数在一定概率水平下所作出的估计。参数估计包括点估计和区间估计。

9. 什么是小概率原理?它在假设检验中有何作用?

小概率原理是指概率很小的事件在一次试验中被认为是几乎不可能发生的，一般统计学中常把概率小于0.05或0.01的事件作为小概率事件。它是假设检验的依据，如果在无效假设H0成立的条件下，某事件的概率大于0.05或0.01，说明无效假设成立，则接受H0，否定H1；如果某事件的概率小于0.05或0.01，说明无效假设不成立，则否定H0，接受H1。

10. 什么叫相关分析？相关系数和决定系数各具有什么意义？

相关分析是用来研究呈平行关系的相关变量之间关系的统计分析方法。相关系数表示变量x和变量y相关的程度及性质。决定系数是相关系数的平方，表示变量x引起y变异的回归平方和占y变异总平方和的比率，它只能表示相关的程度而不能表示相关的性质。

六、计算题

1.下表是某地区4月下旬平均气温与5月上旬50株棉苗蚜虫头数的资料。试建立直线回归方程。               

年份	1969	1970	1971	1972	1973	1974	1975	1976	1977	1978	1979	1980
4月下旬平均气温(x)／℃	19.3	26.6	18.1	17.4	17.5	16.9	16.9	19.1	17.9	17.5	18.1	19.0
5月上旬50株棉蚜虫数(y)／头	86	179	8	29	28	29	23	12	14	64	50	112

解  建立直线回归方程。

计算回归分析所需的6个一级数据：

n=12

由一级数据算得5个二级数据：

计算b值及a值：

建立直线回归方程：

由方程可知，某地区4月下旬平均气温每增加1℃，5月上旬50株棉苗蚜虫就增加18.0836头。

2. 某林场狩猎得到143只野兔，其中雄性57只，雌性86只。试检验该野兔的性别比是否符合1：1？（已知）

解  (1)H0：野兔性别比符合1：1；

     H1：野兔性别比不符合1：1。

     (2)选取显著水平为α=0.05。

     (3)计算统计数χ2 ：根据理论性别比为1：1，可知143只野兔中雄性与雌性理论值均应为

由于df=k-1=2-1=1，故计算χ2时需进行连续性矫正，于是有

(4)查χ2值表，df=1时，，，所以，否定H0，接受H1，认为野兔性别比不符合1：1。

3. 测定一种绵羊的角长。结果为：8.9、6.3、8.7、8.8、9.1、6.2、8.6、7.8、9.2、8.9（cm），试求其平均数、极差、标准差和变异系数。

解：

     

                           

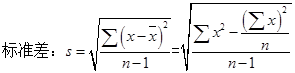
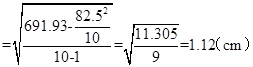
    4.饲料的常规含氮量为2.40％，对一种新饲料的含氮量进行了10次测定，其结果为：2.38，2.38，2.41，2.50，2.47，2.41，2.38，2.26，2.32，2.41(％)。试问该测定结果与饲料常规含氮量有无差别？（已知t0.05（9）=2.262）

根据题目所给数据可算出=2.39％，s=0.0681％。

(1)假设H0：μ=μ0，即该测定结果与常规含氮量没有显著差别；H1：μ≠μ0，即该测定结果与常规含氮量有显著差别。

(2)确定显著性水平α=0.05。

(3)计算统计数：

(4)作出推断：因为lt l< t0.05（9）=2.262，故接受H0，否定H1，认为该测定结果与枝条常规含氮量没有差别。