第八节 R软件的应用
一、确定给定精度实验的最小样本数
例9.9 计算构建二尾置信区间![]() ,
,![]() 的实验样本数?
的实验样本数?
当![]() ,
,![]() ,由下式
,由下式
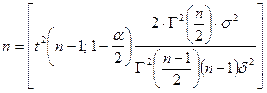 (9-9)
(9-9)
得
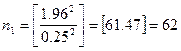
再看一下![]() ,得
,得
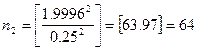
最后,![]() ,得
,得
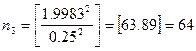
因此,![]() ,稍作修改,我们可以使用R内置函数power.t.test。用
,稍作修改,我们可以使用R内置函数power.t.test。用![]() 表示功效,当
表示功效,当![]() 很大时,因
很大时,因![]() ,修改(9-9)式为
,修改(9-9)式为
![]()
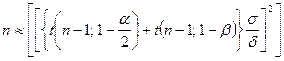 (9-10)
(9-10)
使用R内置函数power.t.test进行计算:
> power.t.test(type = "one.sample", power =0.5, delta = 0.25,
+ sd = 1,sig.level = 0.05, alternative = "two.sided")
One-samplet test power calculation
n =63.4024
delta = 0.25
sd = 1
sig.level = 0.05
power =0.5
alternative = two.sided
为了方便起见,我们提供了一个调用包装器size.t.test,它返回所需的整数大小参数:
> size.t.test(type = "one.sample", power =0.5, delta = 0.25,
sd = 1, sig.level = 0.05, alternative ="two.sided")
[1] 64
因此,我们确定样本量为64。
例如,如果我们随机抽取大小为20的样本,则使用我们的调用包装器到R内建函数delta.t.test给定的半期望宽度![]() ,可以通过以下方式计算:
,可以通过以下方式计算:
> delta.t.test(type = "one.sample", power =0.5, n = 20, sd = 1,
+ sig.level = 0.05, alternative = "two.sided")
[1] 0.4617063
另一方面,如果精度要求声明两个结果限制不能超过![]() ,从参数
,从参数![]() 以给定的概率
以给定的概率![]() ,那么,我们必须选择两尾检测:
,那么,我们必须选择两尾检测:
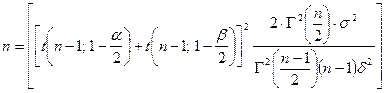 (9-11)
(9-11)
例9.10 我们计算构建双侧置信区间所需的样本量,使用精度要求类型B:
> size.t.test(type = "one.sample", power =0.95, delta = 0.25,
+ sig.level = 0.05, alternative = "two.sided")
[1] 210
例9.11如果我们想要确定配对实验观测的大小,以便间隔的一半期望宽度不能大于![]() ,我们使用
,我们使用![]() 的标准差
的标准差![]() 的估计值作为先验信息。手工进行计算,我们从
的估计值作为先验信息。手工进行计算,我们从![]() 开始;
开始;![]() 。那么我们得到
。那么我们得到![]() ,
,![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ,因此需要27个数据对。
,因此需要27个数据对。
在我们的OPDOE中使用我们的调用封装器size.t.test:
> size.t.test(type = "paired", power = 0.5,delta = 1.2,
+ sd = 3.653, sig.level = 0.05, alternative ="one.sided")
[1] 27
因此,我们确定样本对数为27。
例9.12 我们希望找到一个实验的最小样本数,以构造两个正态分布的期望差异的双侧99%置信区间。我们假设等方差,并从每个群体中取出独立样本,并通过使用(9-12)来确定精度,而对于精度类型B,![]() ,使用(9-13)来确定精度。
,使用(9-13)来确定精度。
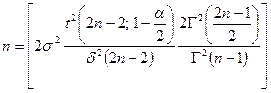 (9-12)
(9-12)
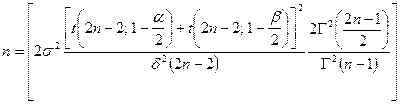 (9-13)
(9-13)
该计算可以分别通过R内置函数power.t.test和调用包装器size.t.test来完成。使用(9-12)可得:
>size.t.test(power = 0.5, sig.level = 0.01, delta = 0.5,
+ sd = 1,type = "two.sample")
[1] 55
使用(9-13)可得:
size.t.test(power= 0.97, sig.level = 0.01, delta = 0.5,
+ sd = 1,type = "two.sample")
[1] 161
备注:如果不能确定两个方差是否相等,那么应该使用下面描述的不等方差的置信区间,正如Rasch等人所建议的那样。
二、概率的置信区间
让我们假设n个独立的实验,其中每个事件都以相同的概率p发生。 对于p的一个![]() 置信区间可以根据这个事件的观测值的个数y来计算为
置信区间可以根据这个事件的观测值的个数y来计算为![]() ,下界
,下界![]() 和
和![]() 上界分别由下式给出。
上界分别由下式给出。
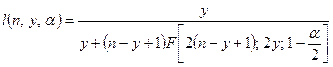 (9-14)
(9-14)
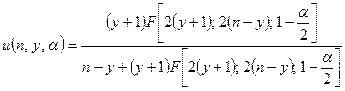 (9-15)
(9-15)
![]() 是具有
是具有![]() 和
和![]() 自由度的F分布的P分位数。当我们使用误差传播定律推导出半期望宽度时,只需要获得所需样本量的近似值。为了近似确定最小样本大小,对p使用近似置信区间的半期望宽度似乎更好。这种间隔由下式给出
自由度的F分布的P分位数。当我们使用误差传播定律推导出半期望宽度时,只需要获得所需样本量的近似值。为了近似确定最小样本大小,对p使用近似置信区间的半期望宽度似乎更好。这种间隔由下式给出
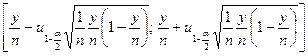 (9-16)
(9-16)
这个间隔有近似一半的期望宽度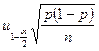 。这个要求小于
。这个要求小于![]() 得出:
得出:
![]() (9-17)
(9-17)
如果对p没有什么了解,我们必须采取最不利的情况p = 0.5,这给出了最小样本量的最大值。 在本章以及方差分析中,这被称为最大值大小(maximinsize)。 计算可以通过OPDOE的函数size.prop.confint完成。
例9.13对于事件A的概率p = P(A),我们需要一个置信区间:“铸铁是有缺陷的”。置信度系数被规定为0.90。如果间隔的期望宽度为:
a)不大于![]() ,p未知?
,p未知?
b)不大于![]() ,当已知至多有10%的铸件存在缺陷时?
,当已知至多有10%的铸件存在缺陷时?
则需要实验多少个铸件?
对于R程序给出所需样本大小为n = 271的情况。如果根据先验知识,我们可以设置p =0.1的上限(情况b),那么我们得到较小最小样本n = 98:
>size.prop.confint(p = NULL, delta = 0.05, alpha = 0.1)
[1]271
>size.prop.confint(p = 0.1, delta = 0.05, alpha = 0.1)
[1]98
差异或更好的标准差是尺度参数;因此,我们用比率替换距离。 一个正态分布的方差![]() 的置信区间,其
的置信区间,其![]() 置信系数为:
置信系数为:
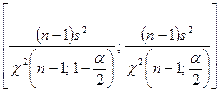 (9-18)
(9-18)
![]() 和
和![]() 是具有n-1自由度的
是具有n-1自由度的![]() 分布的分位数。一半的期望宽度是
分布的分位数。一半的期望宽度是
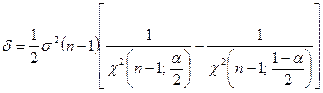 (9-19)
(9-19)
则
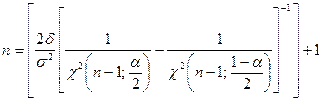 (9-20)
(9-20)
如果我们将精确度定义为置信区间的相对一半期望宽度![]() 与
与![]() 定义为期望的区间中点,然后
定义为期望的区间中点,然后
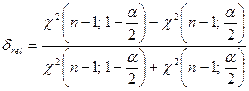 (9-21)
(9-21)
计算可以通过OPDOE函数size.variance.confint完成。
例9.13 如果![]() ,方差的置信区间的一半期望宽度被固定为
,方差的置信区间的一半期望宽度被固定为![]() 和
和![]() ,那么我们需要n = 132个观测值。如果我们要求
,那么我们需要n = 132个观测值。如果我们要求![]() 和
和![]() ,那么我们需要n = 120个观察值。
,那么我们需要n = 120个观察值。
>size.variance.confint(alpha = 0.05, delta = 0.25)
$n
[1] 132
$alpha
[1] 0.05
$delta
[1] 0.25
$deltarel
NULL
>size.variance.confint(alpha = 0.05, deltarel = 0.25)
$n
[1] 120
$alpha
[1] 0.05
$delta
NULL
$deltarel
[1] 0.25
例9.14考虑选择a = 6的正态分布的情况,如果方差相等,但未知。多元独立分布样本![]() ,样本大小为
,样本大小为![]() 。我们如何选择符合以下给出的精度要求的样本大小,
。我们如何选择符合以下给出的精度要求的样本大小,![]() 和
和![]() ,如果我们应用Bechhofer的选择规则:“选择具有最大样本均值的总体”,R程序给出了以下解决方案:
,如果我们应用Bechhofer的选择规则:“选择具有最大样本均值的总体”,R程序给出了以下解决方案:
>size.selection.bechhofer(a = 6, beta = 0.01, delta = 1,
+ sigma =NA)
[1] 17
本章中的R程序必须理解如下。在写出要确定的内容之后,名字以大小开始;这可能是n,但也可以是混合模型中随机因子水平的数量(比如说a)。下一个位置是分类(单向,双向或三向)和分类类型(交叉,嵌套或混合);下一个条目是模型编号(相应部分文本中的编号)。下一个条目是要实验的要素或因素水平组合;例如,a,b或c分别表示因子A,B或C,a![]() b表示相互作用A
b表示相互作用A![]() B。然后遵循精确度要求,包括固定因子水平,最后说明我们是否要计算minimin或maximin的大小。
B。然后遵循精确度要求,包括固定因子水平,最后说明我们是否要计算minimin或maximin的大小。
例如“>size_b.three_way_mixed_cxbina.model_4_a(0.05,0.1,0.5,4,maximin)”意味着我们计算三向混合分类C中的随机因子B的级数的最大值![]() ,模型4实验因子A的影响,C有4个等级,计算的R程序为size_n.one_way.model_1()。
,模型4实验因子A的影响,C有4个等级,计算的R程序为size_n.one_way.model_1()。
>size_n.one_way.model_1(0.05, 0.1, 2, 4, "maximin")
[1] 9
>size_n.one_way.model_1(0.05, 0.1, 2, 4, "minimin")
[1] 5
因此,R的输出给出最小最小样本数![]() 和最大最小尺寸样本数
和最大最小尺寸样本数![]() 。如果随机模型II为
。如果随机模型II为![]() ,
,![]() (单向ANOVA模型)。
(单向ANOVA模型)。
例9.15 我们想要实验六个小麦品种在其产量中没有差异的零假设。对于这个实验,我们可以在四个实验站(简称农场)的每一个处为每个品种使用多个块。这些品种是固定因子A的水平,并且这四个农场也被认为是(块)因子B的固定水平,因为这4个实验站用于这种调查。让我们把精度要求作为I型错误概率![]() ;如果
;如果![]() ,II型错误概率
,II型错误概率![]() 。
。
>size_n.two_way_cross.model_1_a(0.05, 0.1, 1, 6, 4, "maximin")
[1] 9
>size_n.two_way_cross.model_1_a(0.05, 0.1, 1, 6, 4, "minimin")
[1] 4
因此,![]() 和
和![]() 。
。


