第六节 交叉设计
交叉设计，也称为反转实验设计，是指在相同实验中将实验单元分阶段并重复两次的实验设计方法。
在动物实验中，为了提高实验的准确性，有必要在遗传和生理上选择相同或相似的实验动物，但在实践中往往难以满足。为奶牛的泌乳实验选择一些头部品种，性别，年龄和胎儿劣等条件是非常困难的。为了消除个体与实验之间的差异的影响，可以使用交叉设计方法。常用的有2×2和2×3交叉设计，见表9-14和9-15。
表9-14 2×2交叉设计 表9-15 2×3交叉设计
群别 |
时 期 |
群别 |
时 期 | ||||
I |
II |
I |
II |
III | |||
1 |
处理 |
对照 |
1 |
处理 |
对照 |
处理 | |
2 |
对照 |
处理 |
2 |
对照 |
处理 |
对照 | |
一、2×2交叉设计与分析
2×2交叉设计就是两组实验动物分两期一次交叉的实验设计。下面举例说明实验结果的分析方法。
例9.5为了研究新饲料配方对奶牛产奶量的影响，设置对照饲料A1和新饲料配方A2两种处理方式，选取10头条件相似的奶牛，随机分为B1、B2两组，每组5头，并且初步试用期为1周。根据2x2交叉设计实验，实验分为C1、C2两次，每两周一次。实验结果如表9-16所示。实验新的饲料配方，以提高牛奶产量没有影响。
对于2×2交叉实验资料，采用单因素二水平差值d的方差分析法（Lucas）或t检验法进行分析。两种分析方法的无效假设、备择假设均为：
。
（一）方差分析法 此例处理数k=2，重复数r=5。先计算出两个时期产奶量的差d=C1-C2，以及
，见表9-16。
1.计算各项平方和与自由度
矫正数 
总平方和 
处理平方和 
误差平方和 
总自由度 
处理自由度 
误差自由度 
表9-16 例9.5实验结果 （单位：千克/头·日）
时 期 |
C1 |
C2 |
d=C1-C2 | ||
处 理 |
A1 |
A2 |
d1 |
d2 | |
B1
组 |
B11 |
13.8 |
15.5 |
-1.7 | |
B12 |
16.2 |
18.4 |
-2.2 | ||
B13 |
13.5 |
16.0 |
-2.5 | ||
B14 |
12.8 |
15.8 |
-3.0 | ||
B15 |
12.5 |
14.5 |
-2.0 | ||
处 理 |
A2 |
A1 | |||
B2
组 |
B21 |
14.3 |
13.5 |
0.8 | |
B22 |
20.2 |
15.4 |
4.8 | ||
B23 |
18.6 |
14.3 |
4.3 | ||
B24 |
17.5 |
15.2 |
2.3 | ||
B25 |
14.0 |
13.0 |
1.0 | ||
总 和 T1=-11.4 T2=13.2 | |||||
2.列出方差分析表，进行F检验
表9-17 例9.5实验资料方差分析表
变异来源 |
SS |
df |
MS |
F |
F0.01(1, 8) |
处 理 |
60.5160 |
1 |
60.52 |
33.16** |
11.26 |
误 差 |
14.6000 |
8 |
1.83 | ||
总变异 |
75.116 |
9 |
因为处理F值33.16>F0.01(1, 8)，P<0.01，否定
，接受
，表明新配方饲料与对照饲料平均产奶量差异极显著，这里表现为新配方饲料的平均产奶量极显著高于对照饲料的平均产奶量。
（二）t检验法 检验公式为：
（9-5）
其中：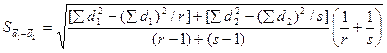
差数平均数差异标准误
r, s分别为两组实验个体数。
此例，r=s=5, 
由df=(r-1)+(s-1)=(5-1)+(5-1)=8查临界t值得：t0.01(8)=3.355，因为|t|=5.7854> t0.01(8)，P<0.01，否定
，接受
，表明新配方饲料与对照饲料平均产奶量差异极显著。检验结果与方差分析法一致。
二、2×3交叉设计与分析
2×3交叉设计就是将实验动物分三期两次交叉的实验设计。对于2×3交叉实验资料，亦采用方差分析法或t检验法进行分析。
例9.6 为了研究饲喂尿素对奶牛产奶量的影响，设置尿素配合饲料A1和对照饲料A2两个处理，选择条件相近的奶牛6头，随机分为B1、B2两组，每组3头，实验分C1、C2、C3三期（每期20天），B1组（B11，B12，B13）按A1—A2—A1顺序给予饲料，B2组（B21，B22，B23）按A2—A1—A2顺序给予饲料，预饲期1周。实验结果列于表9-8，试检验尿素对提高奶牛的产奶量有无效果。
按公式d=C1-2C2+C3分别计算出B1组的差d1和B2组的差d2及T1、T2。两种方法的无效假设与备择假设均为
, 。
（一）方差分析法
此例，处理数k=2，重复数r=3。
1.计算各项平方和与自由度
矫正数 
总平方和 
处理平方和 
误差平方和 
总自由度 
处理自由度 
误差自由度 
表9-18 例9.6实验结果 单位：千克/头·日）
时 期 |
C1 |
C2 |
C3 |
d=C1-2C2-C3 | ||
处 理 |
A1 |
A2 |
A1 |
d1 |
d2 | |
B1
组 |
B11 |
11.32 |
11.36 |
11.31 |
-0.09 | |
B12 |
13.67 |
13.40 |
13.83 |
0.70 | ||
B13 |
18.74 |
16.34 |
16.39 |
2.45 | ||
处 理 |
A2 |
A1 |
A2 | |||
B2
组 |
B21 |
11.65 |
11.19 |
11.12 |
0.39 | |
B22 |
13.57 |
13.87 |
13.41 |
-0.76 | ||
B23 |
11.54 |
10.97 |
10.66 |
0.26 | ||
总 和 T1=3.06 T2=-0.11 | ||||||
2.列出方差分析表，进行F检验
表9-19 例9.6实验资料方差分析表
变异来源 |
SS |
df |
MS |
F |
F0.05(1, 4) |
处 理 |
1.6748 |
1 |
1.6748 |
1.60ns |
7.71 |
误 差 |
4.1727 |
4 |
1.0432 | ||
总变异 |
17.72 |
5 |
F检验结果表明，在对照饲料基础上添加尿素对提高奶牛产奶量效果不显著。
（二）t检验法
2×3交叉实验资料分析的t检验公式与2×2交叉实验资料分析的t检验相同。
此例r=s=3，T1=3.06，T2=-0.11，
，
由df=(r-1)+(s-1)=(3-1)+(3-1)=4查临界t值，得：t0.05(4)=2.776，因为t=1.2672<t0.05(4)，P>0.05，表明在对照饲料上添加尿素与否，奶牛产奶量差异不显著。检验结果与方差分析法相同。
三、交叉设计的优缺点及注意事项
（一）交叉设计的优缺点
1.主要优点 交叉设计可以消除个体与实验时间差异的影响，进一步突出处理效果，提高实验的准确性。因此，交叉设计特别适用于具有较大个体差异的动物实验，如大型动物和兽医实验。另外，交叉实验结果的分析很简单。
2.主要缺点 与拉丁方设计相比，交叉设计无法获得个体差异和实验周期差异的信息，也无法得到各因素之间的交互作用。因此，交叉设计的应用范围有一定的局限性。
（二）应用交叉设计须注意的问题
1.处理因素、时期、个体间不存在交互作用 如果过程因素，周期和个人在交叉实验中有交互作用，这些交互效应将被分类到误差项中，并且误差估计可能会增加，从而降低实验的准确性。
2.要注意实验是否有处理残效 如果实验具有残留效应，则交叉实验不能建立观测值的线性模型条件。为了解决这个问题，我们可以设置合适的实验周期和间歇周期。交叉设计不适合处理残留影响，如破坏性和不可恢复的实验。
3.采用Lucas提出的方差分析法分析2×2、2×3交叉实验资料时要求各实验组动物的头数相等 如在例9.6中，第一组按A1—A2—A1的顺序给予饲料，第二组按A2—A1—A2顺序给予饲料，每头奶牛被分配到哪一组，是随机确定的，但两个组的奶牛头数必须相等。只有这样才能通过Σd1j-Σd2j而使实验期的效应相互抵消。
