第九节 R软件的应用 

       回归分析是用于建模一组输入（或预测变量）变量与一个或多个输出（响应）变量之间关系的统计技术。称为简单线性回归或直线回归的最简单形式的回归分析涉及单个输入因子X（“回归”）和单个输出变量Y（“响应”）之间的统计建模。我们讨论简单的线性回归以及如何在这里进行详细的分析。

首先让我们考虑如何在生成正式回归模型之前简单看看两个变量之间的关系。

一、相关性

相关度量是变量之间关联的度量。值得注意的是，关联是一个没有因果关系的概念。两个变量可以很好地相关，但没有因果关系。例如，在温暖的天气里，冰淇淋的消费量和蚊子的数量都会增加。测量这些数量的变量将具有高度相关性。然而，这种关系不过是偶然的关系，并没有进一步的统计利益。

尽管如此，查看相关性确实为查看变量之间的关系提供了有用的初步分析。相关度量被称为相关系数，通常由字母r表示。有三种最常用的相关度量：皮尔逊相关系数，斯皮尔曼的和肯德尔的。皮尔逊相关系数由数学公式确定：

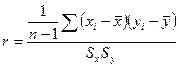                （8-21）

       其中n是数据点的数量，和分别是x和y数据的标准偏差，和是数据的平均值。斯皮尔曼的和肯德尔的是非参数相关系数，并且基于数据的等级。

所有三个相关度量值都在1和-1之间，其中1是完美的正相关，-1是完美的负相关，0表示没有相关性。所有三种相关性都衡量两个变量之间线性关系的强度。在完全相关为1的情况下，（x，y）数据点都完全位于具有正斜率的线上。这通常不会发生在真实数据上。例如，考虑小数据集geneCorrData（这是作为rbioinfo软件包的一部分提供的，该软件包包含在R的早期版本中相同处理条件下两种基因的时间过程的表达式测量，但已经退役）。我们可以使用R来分析这两个功能相关的基因表达的相关性，以研究它们如何一起表达。

首先，看数据，似乎有关系吗？

>geneCorrData=read.table("rdata.txt",head=TRUE)

> geneCorrData

   gene1 gene2

1  -1.06 -1.08

2  -0.81 -1.02

3  -0.48 -0.39

4  -0.42 -0.48

5  -0.30 -0.58

6  -0.35 -0.24

7  -0.31 -0.05

8  -0.18 -0.33

9  -0.20  0.51

10 -0.11 -0.53

11 -0.09 -0.47

12  0.16  0.10

13  0.45  0.39

14  0.53  0.11

15  0.67  0.52

16  0.80  0.34

17  0.87  1.08

18  0.92  1.21

如图8-3所示，它可以对数据进行简单的绘制帮助理解相关性。

> plot(geneCorrData$gene1,geneCorrData$gene2)

 

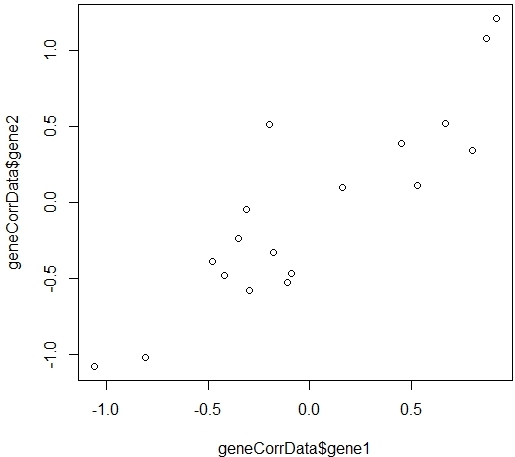
图8-3 gene1和gene2相关关系图（1） 

情节直观地表明存在关系的证据，但没有量化它。我们使用相关系数来测量基因1和基因2表达值之间线性关系的强度。要做到这一点，我们可以使用R函数cor.test。默认情况下，测试计算皮尔逊相关系数，但其他系数可以使用可选的方法参数指定。

> cor.test(geneCorrData$gene1,geneCorrData$gene2)

        Pearson'sproduct-moment correlation

data: geneCorrData$gene1 and geneCorrData$gene2

t = 7.5105, df = 16, p-value =1.246e-06

alternative hypothesis: true correlation is not equal to0

95 percent confidence interval:

 0.70715600.9556856

sample estimates:

      cor

0.8826268

这个相关性，0.88或0.80取决于您使用哪种度量标准，非常强大。它表示基因1（X值）和基因2（Y值）的表达值之间的关联是正值，并且值高度相关（一个值上升，另一个值也是如此）。它没有做的是创建任何类型的统计模型，它与我们如何预测新的X数据点的新Y值有关。一个简单的线性回归模型需要做到这一点。

二、基本简单线性回归模型

当然，在你的数学生涯的某个阶段，可能在代数课上，你遇到了一条直线y = mx + b的方程。在这个等式中，m是线的“斜率”（在y上随着x的变化而变化），b是y轴与线相交的线的“截距”。虽然直线模型对于代数学是完美的，但在现实世界中，找到这种完美的线性关系几乎是不可能的。大多数现实世界中的关系不是完美的线性模型，但是x和y之间的关系更类似于不完美模型。在这种情况下，问题字面上是“你在哪里画线？”。简单线性回归是正确回答这个问题的统计技术。

简单线性回归是现实世界中X和Y之间的统计模型，其中存在与随机变量相关的随机变量。为了研究X和Y之间的关系，最简单的关系是直线关系，而不是更复杂的关系，如多项式。因此，在大多数情况下，我们想尝试将数据拟合成线性模型。如图8-3所示绘制X对Y是确定线性模型是否合适的第一步。有时候，如果数据不能在原始测量尺度上进行转换（通常采用对数或其他数学方法），则可以转换数据以拟合线性模式。确定X和Y之间的直线关系是否合适是第一步。第二步，确定使用的线性模型，就是确定代表关系的最佳拟合线。

三、拟合回归模型

很明显，根据图8-3，你可以简单地拿一把尺子画出一条线，根据你的主观看法，最好的方法是通过数据。这种方法很容易出错，不太可能会产生“最佳拟合”线。因此需要更复杂的方法。为了拟合回归模型，我们做了一些假设，其中包括：

1.对于任何给定的X值，Y的真实平均值取决于X，可写为。在回归中，该线表示Y的平均值而不是单个数据值。

2.每个观察都独立于其他变量，且。

3.我们假设X和Y的均值之间存在线性关系。Y的平均值由直线关系决定，可写为：，其中是线的斜率和截距（注意这与y = b + mx非常相似，即直线的方程）。

4.的方差是恒定的（同方差性质）。

5.响应变量通常是正态方式分布，方差恒定（见属性4）。

让我们建立在第三个假设上。Y的实际观察值与的平均值相差一个误差项（反映随机变化）。我们可以这样写：

误差，是平均线和实际的数据值之间的差异。我们称这些误差为残差。为了拟合回归模型，我们有要估计的参数。在这种情况下，我们需要优良的估计来估计，线的斜率和，y轴截距。我们有一种特殊的估计方法，称为最小二乘法。有时简单线性回归被称为最小二乘回归。最小二乘估计最小化点与线之间的垂直距离的平方和，这与使剩余值的平方最小化相对应。以上用于值的希腊字母的模型是理论模型。对于理论估计参数，我们约定使用小写b（备选符号在希腊字母上使用帽子，例如）表示这些是基于数据而非理论值的估计值。最小二乘估计的公式如下：

斜率估计：

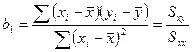
分子也称为xy平方和（），分母称为x平方和（）。

截距估计：

当然，用大数据集进行这种计算是很乏味的。但是，不需要手动进行这些计算，因为R提供简单的功能来执行它们。

再次，与方差分析一样，我们将使用线性模型函数lm。为了在R中执行简单的线性回归分析，对于前面描述的基因表达数据，简单地将感兴趣的y和x数据向量建模为lm（y〜x）如下：

> geneLM<-lm(geneCorrData$gene2~geneCorrData$gene1)

> geneLM

Call:

lm(formula = geneCorrData$gene2 ~ geneCorrData$gene1)

Coefficients:

      (Intercept) geneCorrData$gene1 

         -0.05541         0.97070 

在上面的输出中，R计算了b0项（-0.05541），即截距和斜率（0.9707）。这些术语被称为系数。你可以使用给出的系数和经验数据的公式来验证这些结果。将创建的线性模型对象存储在新变量中以便进一步分析是一个不错的主意。

绘制回归线使分析更有趣。我们可以用一个简单的绘图函数来做到这一点，然后为y添加一个具有拟合数据值的行。

> plot(geneCorrData$gene1,geneCorrData$gene2)

> lines(geneCorrData$gene1,fitted(geneLM))

为了让事情更有趣，我们可以添加将经验数据连接到回归线的部分。这些线段的长度是残差或误差，表示从经验数据到拟合回归值（y线的平均值）的距离。

> segments(geneCorrData$gene1,fitted(geneLM),geneCorrData$gene1,geneCorrData$gene2,lty=2)

> title("Fitted Model with Residual LineSegments")

图8-4显示了结果图。这个模型允许我们根据公式的经验x值预测新的y数据（用来表示它是一个估计值）。

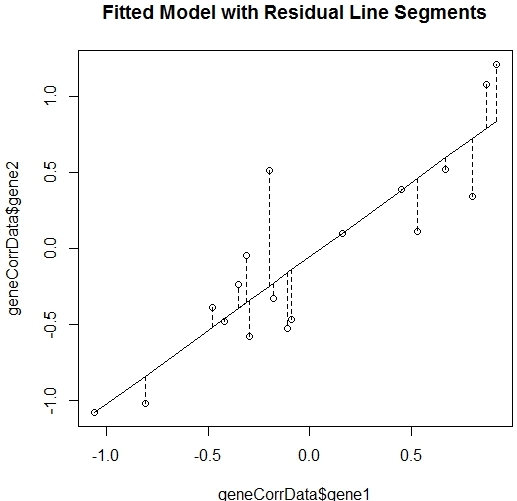
图8-4 gene1和gene2相关关系图（2）

 

请注意，回归是了解现有因果关系而不是创建它们的工具。研究人员错误地认为两个变量之间存在因果关系只是因为他们可以找到一个很好的与变量相关的回归模型。

如果您想查看拟合值和残差，则R提供fitted和resid函数。使用包含线性模型对象的已保存变量提供这些函数以获取结果的输出：

> fitted(geneLM)

 1           2           3           4           5           6

-1.08435135 -0.84167628-0.52134519 -0.46310317 -0.34661914 -0.39515415

 7          8           9          10          11          12

-0.35632614 -0.23013511-0.24954911 -0.16218609 -0.14277208  0.09990299

 13         14          15          16          17          18

 0.38140607 0.45906209  0.59496013  0.72115116 0.78910018  0.83763519

> resid(geneLM)

 1             2             3             4             5

 4.351347e-03 -1.783237e-01  1.313452e-01 -1.689683e-02 -2.333809e-01

 6             7             8             9            10

 1.551542e-01 3.063261e-01 -9.986489e-02 7.595491e-01 -3.678139e-01

  11           12            13            14            15

-3.272279e-01  9.701311e-05 8.593934e-03 -3.490621e-01 -7.496013e-02

  16            17            18

-3.811512e-01  2.908998e-01 3.723648e-01

事实上，如果将拟合值和残差值相加，则可以得到经验性Y数据值（gene2）。

> fit<-fitted(geneLM)

> res<-resid(geneLM)

> sumFnR<-fit+res

> compare<-data.frame(sumFnR,geneCorrData$gene2)

> compare

   sumFnRgeneCorrData.gene2

1   -1.08              -1.08

2   -1.02              -1.02

3   -0.39              -0.39

4   -0.48              -0.48

5   -0.58              -0.58

6   -0.24              -0.24

7   -0.05              -0.05

8   -0.33              -0.33

9    0.51               0.51

10  -0.53              -0.53

11  -0.47              -0.47

12   0.10               0.10

13   0.39               0.39

14   0.11               0.11

15   0.52               0.52

16   0.34               0.34

17   1.08               1.08

18   1.21               1.21

四、测试回归模型

一旦我们有了回归模型，我们通常希望做一些推理测试和分析，看看模型是否确实是合适的，或者我们是否应该相应地调整模型。在R中，lm函数不仅仅是一个普通函数。它是创建模型对象的特殊类型的函数。那些熟悉面向对象编程的人都知道封装原理，信息被隐藏在对象内部。创建时的线性模型对象包含可以用其他函数提取的隐藏信息。汇总函数可用于提取线性模型对象的细节。这些详细信息包括用于诊断回归拟合的信息。将汇总函数应用于我们的线性模型对象会产生以下输出：

> summary(geneLM)

Call:

lm(formula = geneCorrData$gene2 ~ geneCorrData$gene1)

Residuals:

Min      1Q Median     3Q   Max

-0.3811 -0.2196 -0.0084 0.1492  0.7595

Coefficients:

                  Estimate Std. Error t value Pr(>|t|)   

(Intercept)       -0.05541    0.07330  -0.756   0.461   

geneCorrData$gene1 0.97070    0.12925   7.511 1.25e-06 ***

---

Signif. codes:  0‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 

Residual standard error: 0.311 on 16 degrees of freedom

Multiple R-squared: 0.779,     AdjustedR-squared:  0.7652

F-statistic: 56.41 on 1 and 16 DF,  p-value: 1.246e-06

输出的第一部分只是说明模型。下一节是残差的汇总。经常在回归中，我们看看残差的分布，检查正态性的假设。分布应该以零为中心，所以中间值应该接近于零，对我们的数据也是如此。

通过查看残差分布来检查正态性的另一个好方法是做一个残差Q-Q图来寻找线性模式： 

图8-5 gene1和gene2相关关系图（2）

> qqnorm(resid(geneLM))

图8-5显示了结果，这似乎是合理的线性的，表明模型的正态假设没有被违反。这是一个很好的模型适合的迹象之一。Q-Q图上的非线性模式使人们对正态性假设产生怀疑。这可能或可能不会表明模型拟合存在问题，但值得进一步探索。

用于测试简单线性回归模型的摘要输出的另一部分是系数部分。本节重复斜率和截距系数的最小二乘估计值，但也给出了这些值的统计检验结果的输出，其中使用t检验统计值和检验统计量的p值。

这里有趣的测试是在斜坡上进行的测试，该测试用于测试斜率是否明显不同于零。在这种情况下，当p值为1.25e-06时，我们的斜率与零点有很大的不同。然而，如果这个检验提供了一个微不足道的p值（0.05或更高），这就怀疑x和y之间是否存在强的线性关系，并且可能没有关系，或者可能是另一种类型的模型更适合。截距测试对实践没有多大意义。

五、广义线性模型

本质上，方差分析和回归分析实际上是一回事。两者都是通过线性关系将响应（Y）与输入（X）相关联的线性模型。在上面的例子中，我们研究了一个输入变量的情况，尽管这可以很容易地扩展为包含多个输入变量。方差分析和回归都采用统一的形式。

输出是输入变量和误差项的线性函数。线性模型有几十种不同的形式，这是高级统计课程的主题。在线性模型的所有情况下，“拟合”函数在参数中也是线性的。尽管输入变量本身不需要是线性的并且可以具有除1以外的指数。其中在系数中不遵循线性关系被称为非线性模型。

在生物信息学中，线性模型的经常出现在定量遗传学应用中，如QTL作图。ANOVA模型可用于设计实验和分析微阵列数据。R具有处理各种线性和非线性回归模型的广泛功能，许多软件包专用于特定的高级回归建模应用程序。表15-3列出了选择软件包。 

表8-3 线性模型有关函数                                                     

包	函数	功能
Base	lm()	线性回归模型
Base	glm()	广义线性模型
survival	coxph()	考克斯模型
	survreg()	生存模型
	clogit()	条件逻辑回归
nlme	lme()	线性混合效应模型
	nlme()	非线性混合效应模型
gee	gee()	广义估计方程
rmeta	Various	Meta分析模型（固定效应，随机效应）