第七节 曲线回归 

曲线回归分析（curvilinear regression analysis）的基本任务是通过两个相关变量x与y的实际观测数据建立曲线回归方程，以揭示x与y间的曲线联系的形式。

曲线回归分析最困难和首要的工作是确定变量与x间的曲线关系的类型。通常通过两个途径来确定：1.利用生物科学的有关专业知识，根据已知的理论规律和实践经验。例如，细菌数量的增长常具有指数函数的形式： ；幼畜体重的增长常具有“S”型曲线的形状，即Logistic曲线的形式等。2.若没有已知的理论规律和经验可资利用，则可用描点法将实测点在直角坐标纸上描出，观察实测点的分布趋势与哪一类已知的函数曲线最接近，然后再选用该函数关系式来拟合实测点。

对于线性曲线函数类型，曲线回归分析的基本过程是将x或y转换为变量，然后对新变量进行线性回归分析，建立线性回归方程并进行显著性检验和区间估计，最后恢复新的变量为原始变量。原始变量的曲线回归方程和置信区间由新变量的线性回归方程和置信区间导出。

以下是几种常用的线性曲线函数类型及其模式，以及线性曲线，用于选择曲线回归分析。

1.双曲线函数     

若令，则可将双曲线函数直线化为：

2.幂函数 (a>0)

若对幂函数两端求自然对数，得：

并令，则可将幂函数直线化为：

3.指数函数或（a>0）

（1）若对指数函数两端求自然对数，得：

并令，则可将其直线化为：

（2）若对指数函数两端取自然对数，得：

并令，则可将其直线化为：

4.对数函数

令，则将其直线化为

5.Logistic生长曲线

若将Logistic生长曲线两端取倒数，得：             

，

对两端取自然对数，得

令、、，可将其直线化为：                       

例8.4 测定黑龙江雌性鲟鱼体长（cm）和体重（kg），结果如8-3表所示，试对鲟鱼体重与体长进行回归分析。

1.根据实际观测值在直角坐标纸上作散点图，选定曲线类型  此例的散点图见图8-2。从散点图实测点的分布趋势看出它比较接近幂函数曲线图形，因而选用来进行拟合。取，，则可将其直线化为：。

2.对进行直线回归分析 

表8-3 鲟鱼体长与体重数据表                                                                                                            

序号	体长   （x）	体重   （y）
1	70.70	1.00	1.8495	0	1.16305	-0.16306
2	98.25	4.85	1.9923	0.6857	3.86206	0.98794
3	112.57	6.59	2.0514	0.8189	6.34346	0.24654
4	122.48	9.01	2.0881	0.9547	8.62909	0.38091
5	138.46	12.34	2.1413	1.0913	13.49604	-1.15604
6	148.00	15.50	2.1703	1.1903	17.20854	-1.70854
7	152.00	21.25	2.1818	1.3274	18.96637	2.28363
8	162.00	22.11	2.2095	1.3446	23.92790	-1.81970

根据表8-3计算得：

 

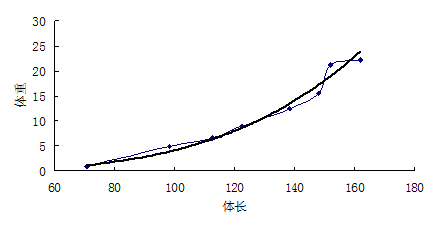
图8-2 鲟鱼体长与体重散点图及回归曲线图

与的相关系数为：

 

当df=n-2=8-2=6时，，，P<0.01，表明yˊ与xˊ间存在极显著的线性关系。又因为：

得，yˊ与xˊ的直线回归方程为：

3.将变量xˊ、yˊ还原为x、y

       

即：                 

 

4.曲线配合的拟合度曲线配合的好坏，即所配曲线与实测点吻合的好坏，取决于离回归平方和与y的平方和的比例大小。若这个比例小，说明所配曲线与实测点吻合程度高，反之则低，我们把数量1与这个比值之差定义为曲线回归的相关指数，记为R2，即：

                （8-21）

相关指数R2的大小表示了回归曲线拟合度的高低，或者说表示了曲线回归方程估测的可靠程度的高低。

对于例8.4先根据回归方程计算出各个回归估计值和，见表8-3，计算出相关指数R2为：

表明曲线回归方程的拟合度是比较高的，或者说该曲线回归方程估测的可靠程度比较高。

对于同一组实测数据，根据散点图的形状，可用几个相近的曲线进行拟合，同时建立几个曲线回归方程，此时可根据R2的大小和生物学等专业知识，选择既符合生物学规律，拟合度又较高的曲线回归方程来描述这两个变量间的曲线关系。