第六节 自变量的选择与逐步回归 

在多元线性回归分析中，一方面，为了获得更全面的信息，我们总是希望模型包含尽可能多的变量；另一方面，自变量越多，收集数据越困难，成本越高，一些自变量与其他自变量重叠。如果将它们引入到模型中，不仅会增加计算量，而且会对模型参数的估计和模型的预测产生负面影响。这样，我们自然希望模型能够选择最合适的自变量，建立合理而简单实用的回归模型。这里我们介绍一些参数选择的标准以及“最优”变量子集的相应计算方法。

1.自变量选择对估计和预测的影响

设我们研究某一实际问题时，根据经验或专业知识，确定一切可能对因变量有影响的因素共有个，记为，它们与一起构成线性回归模型

               （8-13）

我们称这个与所有自变量的回归模型为全模型。

      如果我们从所有可供选择的个变量中挑出个，记为，建立如下的回归模型

               （8-14）

我们称其为选模型。

       当用回归分析来解决问题时，自变量的选择问题可以看作是用整个模型还是模型来描述实际问题。这里我们给出一些没有证据的结论，并且说明了自变量的选择对因变量的参数估计和预测的影响。

（1）该模型是正确的，并滥用所选模型。

结论1：当整个模型正确时，选择模型回归系数的最小二乘。估计值是对整个模型的相应参数的有偏估计，并且模型的预测是有偏差的。

结论2：当整个模型正确时，所选模型的参数估计和预测残差与均方差具有较小的方差。

（2）正确选择模型并滥用整个模型的情况。如果模型是正确的，则参数估计和预测值都是无偏的，并且整个模型的参数估计和预测是有偏差的。此外，整个模型的预测值的方差和均值方差大于所选模型的相应方差。

上述结论告诉我们，失去对因变量影响不大的自变量是有利的，但建立回归方程时难以观察到。    

（3）自变量的选择准则

若在一个回归问题中有个变量可供选择，那么我们可以建立个不同的一元线性回归方程，个不同的二元线性回归方程，……，个元线性回归方程，所有可能的回归方程共有

个，前面提到的多元线性回归中选变量也即选模型，即从这个回归方程中选取“最优”的一个，为此就需要有选择的准则。

下面从不同的角度给出选择的准则。

从拟合角度考虑，可以采用修正的复相关系数达到最大的准则。

       准则1  修正的复相关系数达到最大。

       与这个准则等价的准则是：均方残差MSE达到最小，因为

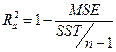
从这个关系式容易看出，达到最大时MSE达到最小。

从预测角度考虑，可以采用预测平方和达到最小的准则以及准则。

准则2  预测平方和达到最小。

预测平方和（PredictionSum of Squares）准则的基本思想是：对于给定的某个自变量，在样本数据中删除第组观测值后利用这个自变量和的其余组观测值建立线性回归方程，并利用所得的回归方程对做预测，若记此预测值为，则预测误差为

依次取，则得到个预测误差。如果包含这个自变量的回归模型预测效果较好，则所有的误差平方和达到或接近最小。即选取使得

达到或接近最小的回归方程作为最优回归方程。

准则3 定义统计量为

        其中是包含个自变量的回归方程的残差平方和，表示含有所有个自变量的回归方程的均方残差。准则要求选择值小，且 小的回归方程。

       从极大似然估计的角度考虑，可以采用赤池信息量准则（AIC准则）。

       准则4（AIC准则）赤池信息量达到最小。

       这个准则由日本统计学家赤池（Akaike）提出，人们称它为AkaikeImformation Criterion，简称为AIC。AIC准则通常定义为

其中表示模型的对数似然函数的极大值，表示模型中独立的参数的个数。

       在实用中，也经常用下式计算赤池信息量

选择AIC值最小的回归方程为最优回归方程。

准则5施瓦茨信息准则（SchwarzCriterion，SC），其定义分别为：

这个准则均要求仅当所增加的解释变量能够减少SC值时才能在原模型中增加该解释变量。显然，与调整的可决系数相仿，如果增加的解释变量没有解释能力，则对残差平方和的减小没有多大帮助，但增加了待估参数的个数，这时可能到SC的值增加。

（4）逐步回归

当自变量的数量不长时，使用一些标准从所有可能的回归模型中找到最优回归方程是可行的。但是如果自变量的数量更多，找到所有的回归方程并不容易。为此，人们提出了一些简单实用的方法来快速选择最优方程，我们简要介绍了“正向法”和“后向法”，然后详细介绍了“逐步回归法”。

①前进法和后退法

前进法的思想是这样的：设所考虑的回归问题中，对因变量有影响的自变共有个，首先将这个自变量分别与建立个一元线性回归方程，并分别计算出这个一元回归方程的偏检验值，记为，若其中偏值最大者（为方便叙述起见，不妨设为）所对应的一元线性回归方程都不能通过显著性检验，则可以认为这些自变量不能与建立线性回归方程；若该一元方程通过了显著性检验，则首先将变量引入回归方程；接下来由与以及其他自变量建立个二元线性回归方程对这个二元回归方程中的的回归系数做偏检验，检验值记为，若其中最大者（不妨设为）通过了显著性检验，则又将变量引入回归方程，依此方法继续下去，直到所有未被引入方程的自变量的偏值都小于显著性检验的临界值，即再也没有自变量能够引入回归方程为止。得到的回归方程就是最终确定的方程。

后退法与前进法相反，首先用个自变量与建立一个回归方程，然后在这个方程中剔除一个最不重要的自变量，接着又利用剩下的个自变量与建立线性回归方程，再剔除一个最不重要的自变量，依次进行下去，直到没有自变量能够剔除为止。

前进法和后退法都有其不足，人们为了吸收这两种方法的优点，克服它们的不足，提出了逐步回归法。

②逐步回归法

逐步回归法的基本思想是有进有出，具体做法是将变量一个一个得引入，引入变量的条件是通过了偏统计量的检验。同时，每引入一个新的变量后，对已入选方程的老变量进行检验，将经检验认为不显著的变量剔除，此过程经过若干步，直到既不能引入新变量，又不能剔除老变量为止。

设模型中已有个自变量，记这个自变量的集合为，当不在中的一个自变量加入到这个模型中时，偏统计量的一般形式为

            （8-15）

下面我详细叙述逐步回归法的具体步骤。

首先，根据一定显著水平，给出统计量的两个临界值，一个用作选取自变量，记为；另一个用作剔除自变量，记为。一般地，取，然后按下列步骤进行。

        第一步：对每个自变量，拟合个一元线性回归模型

                   （8-16）

这时，相当于统计量（8-15）中集合为空集，因此，，故，，对每一个，计算

                （8-17）

设

        若，则选择含自变量的回归模型为当前模型，否则，没有自变量能进入模型，选择过程结束，即认为所有自变量对的影响均不显著。

        第二步：在第一步的选出模型的基础上，再将其余的个自变量分别加入到此模型中个，得到个二元回归方程，计算

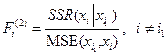              （8-18）

设

        若，则选取过程结束。第一步选择的模型为最优模型。若，则将自变量选入模型中，即得第二步的模型

              （8-19）

        进一步考察，当进入模型后，对的影响是否仍然显著。为此计算

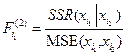                （8-20）

若，则剔除。这时仅含有的回归模型为当前模型。

第三步：在第二步所选模型的基础上，在将余下的个自变量逐个加入，拟合各个模型并计算统计量值，与比较决定是否有新变量引入，如果有新变量进入模型，还需要检验原模型中的老变量是否因这个新变量的进入而不再显著，那样就应该被剔除。

        重复以上步骤，直到没有新的自变量能进入模型，同时在模型之中的老变量都不能剔除，则结束选择过程，最后一个模型即为所求的最优回归模型。