第五节 多元线性回归统计模型 

在线性回归模型中，我们只讨论包含解释变量的线性回归模型，即假设解释变量仅受一个因素的影响。但在现实生活中，解释变量通常受到多种因素的影响。在分析这些问题时，只有一元线性回归模型不能反映变量之间的真实关系，因此我们需要使用多元线性回归模型进行定量分析。

1.多元回归数学模型

n组观测数据：

……

代入上式得：

……

其中，独立且。

用矩阵表示：

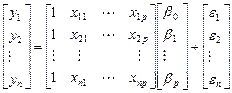
简写为

用最小二乘法求的估计，为此，令

其中    为误差平方和

其中

可得：

2.假定条件

与一元线性回归模型的基本假定相似，为保证得到最优估计量，多元线性回归模型应满足以下假定条件：

假定1 随机误差项满足均值为零，其方差相同且为有限值。

假定2 随机误差项之间相互独立，无自相关。

假定3 解释变量，之间线性无关，即解释变量的样本观测值矩阵式满秩矩阵，否则称解释变量之间存在多重共线性（与课本假定7合并）。

假定4 解释变量，是确定性变量，与误差项彼此之间相互独立。

假定5 解释变量是非随机变量，且当，Q是一个有限值的非奇异矩阵。

假定6 随机误差项服从正态分布。

假定7 回归模型是正确设计的。

3.关于多元线性回归模型中样本容量的问题

（1）最小样本容量

在多元线性回归模型中，样本容量必须不少于模型中解释变量的数目（包括常数项），这就是最小样本容量，即：。

（2）满足基本要求的样本容量

一般经验认为，当或者至少时，才能说满足模型估计的基本要求。

4.多元可决系数与调整后的多元可决系数

类似于一元线性回归模型的情形，我们对估计的回归方程关于样本观测值的拟合优度进行检验，而检验的统计量是可决系数。因是多元回归，样本可决系数就称为多元可决系数。

对于多元线性回归模型的情形，一元线性回归模型的总离差平方和的分解公式依然成立，即：

TSS= ESS +RSS

其中，TSS的自由度为n-1，n表示样本容量，

       ESS的自由度为k，k表示自变量的个数，

RSS的自由度为n-k-1。

我们在模型应用中发现，如果在模型中增加一个解释变量，往往会增大。这是因为残差平方和往往随着解释变量个数的增加而减少，至少不会增加。这就给人一个错觉：要使模型拟合得好，只要增加解释变量就可以了。但是，现实情况往往是，由增加解释变量个数引起的的增大与拟合好坏无关，因此，在多元线性回归模型之间比较拟合优度，就不是一个合适的指标，必须加以调整。

在样本容量一定的情况下，增加解释变量必定使得自由度减少，所以调整的思路是将残差平方和与总离差平方和分别处以各自的自由度，以剔除变量个数对拟合优度的影响。

定义调整的多元可决系数如下：

当模型中增加一个自变量，如果RSS/(n-k-1)变小，因而使增大，便可认为这个自变量对因变量有显著影响，应该放入模型中，否则，应予抛弃。

在样本容量一定的情况下，具有如下性质：

（1）若；

（2）可能出现负值。如时，。显然，负的拟合优度没有任何意义，在此情况下，取

在实际中，或越大，模型拟合得就越好，但拟合优度不是评价模型优劣的唯一标准。因此，我们不能仅根据或的大小来选择模型。

5.多重共线性的处理

多元线性回归模型中，假定自变量之间线性无关，因而资料矩阵是满秩的。如果存在不全为零的个常数，使得

则自变量之间存在着完全的多重共线（Multicollinearity）。在实际问题中完全共线性的情况并不多见，常见的是近似的多重共线关系，即存在不全为零的个常数，使得

如果回归模型存在完的多重共线性，则资料阵的秩，故不存在，无法得到回归参数的估计量。对于近似多重共线性的情况，此时虽有，但，从而矩阵的主对角线上的元素很大，使得估计的参数向量的协方差阵的对角线上元素也很大，导致普通最小二乘参数估计量并非有效。

如何检验是否存在多重共线性？已经由不少的可行的方法，目前常用的有方差扩大因子法和特征根判别法.在此只介绍方差扩大因子（VIF）法。

对自变量做中心标准化处理，则为自变量的相关矩阵，记

称其对角线元素为自变量的方差扩大因子（Variance Inflation Factor），其中是把作为因变量与其余个自变量做线性回归所得到的复相关系数。反映了没个变量所受到的多重共线性的影响的大小。对每一个自变量，都有。也可以用个自变量所对应得方差扩大因子的平均数来度量多重共线性。当远远大于1时，就表示存在严重的多重共线性问题。

当发现自变量存在严重的多重共线性时，可以通过剔除一些不重要的自变量、增大样本容量、对回归系数做有偏估计（如采用岭回法、主成分法、偏最小二乘法等）等方法来克服多重共线性。

6.统计检验

F检验：

为了从总体上检验模型中被解释变量与解释变量之间的线性关系是否显著成立，检验的原假设为：（k表示方程中回归系数的个数，也可以称为自变量的个数）若成立，则模型中被解释变量与解释变量之间不存在显著的线性关系。

备择解释为：不全为零。

若原假设成立，则检验统计量：

这是自由度为的F分布，对于预先给定的显著水平a，可以从F分布表中查出相应的自由度。

设检验水平为a，则检验规则是：

若，接受原假设；

若，则接受备选假设。

F与的关系：

，   

由公式，可以看出，F与成正比，越大，F值也越大。即总体的F检验越显著（F值越大），的值也越大，回归方程拟合得就越好，所以，F检验可以看作是对拟合优度的检验。

回归系数的显著性检验t检验

对于多元线性回归模型，整体回归方程的线性关系的显著性并不意味着每个解释变量对解释变量都有显著影响。因此，有必要从模型中去除那些对解释变量没有显著影响的解释变量，只留下对解释变量有显著影响的解释变量，从而建立一个更简单和更合理的多元线性回归模型。

如果一个解释变量对被解释变量的影响不显著，则对应于该解释变量的回归系数的值等于0。因此，我们只要检验一个解释变量的回归系数的值是否为0就可以了。

检验原假设：；

备择假设：

判别标准，若，接受原假设；若，接受备择假设。