第四节 一元正态线性回归统计模型
对于每个Y的观察值![]() 来说,由于总是带有随机误差,观察值就应该是在均值的基础上再加上一个随机误差,一元线性回归模型的一般形式,即:
来说,由于总是带有随机误差,观察值就应该是在均值的基础上再加上一个随机误差,一元线性回归模型的一般形式,即:
![]() (8-6)
(8-6)
一元线性回归方程为:![]()
当对![]() 与
与![]() 进行n次独立观测后,可取得n对观测值
进行n次独立观测后,可取得n对观测值![]() 则有
则有![]()
回归分析的主要任务是通过n组样本观测值![]() 对
对![]() 进行估计。一般用
进行估计。一般用![]() 分别表示
分别表示![]() 的估计值。
的估计值。
称![]() 为
为![]() 关于
关于![]() 的一元线性回归方程(简称为回归直线方程),
的一元线性回归方程(简称为回归直线方程),![]() 为截距,
为截距,![]() 为经验回归直线的斜率。
为经验回归直线的斜率。
引进矩阵的形式:
设
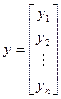 ,
, ,
,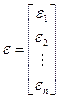 ,
,![]()
则一元线性回归模型可表示为:
![]()
通常假定![]() 满足
满足
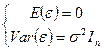
其中![]() 为
为![]() 阶单位阵。
阶单位阵。
为了得到![]() 更好的性质,我们对
更好的性质,我们对![]() 给出进一步的假设(强假设),设
给出进一步的假设(强假设),设![]() 相互独立,且
相互独立,且![]() ,由此可得:
,由此可得:![]() 相互独立,且
相互独立,且![]() 。
。
一、参数α和β的估计
模型中的α和β是参数,一般不知道。由于只能得到有限的观察数据,无法算出准确的α与β的值,只能求出估计值a和b,并得到![]() 的估计值为:
的估计值为:
![]() (8-7)
(8-7)
![]() 和
和![]() 应使残差
应使残差![]() 最小。为了避免使正负ei互相抵消,定义使残差平方和
最小。为了避免使正负ei互相抵消,定义使残差平方和![]() 达到最小的直线为回归线,即令:
达到最小的直线为回归线,即令:
![]() ,且
,且![]() 对a、b的一阶偏导数等于0
对a、b的一阶偏导数等于0
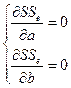
得:
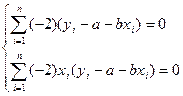
整理后,得
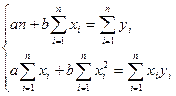 (8-8)
(8-8)
解此方程,得:
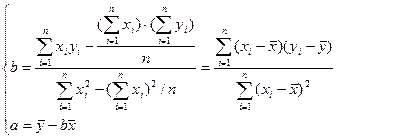
这种方法称为最小二乘法
记
![]() ,称为X的校正平方和;
,称为X的校正平方和;
![]() ,称为Y的总校正平方和;
,称为Y的总校正平方和;
![]() ,称为校正交叉乘积和,
,称为校正交叉乘积和,
则:
![]() (8-9)
(8-9)
a叫样本回归截距,是回归直线与y轴交点的纵坐标,当x=0时,![]() 。
。
b叫样本回归系数,表示x 改变一个单位,y平均改变的数量;b 的符号反映了x影响y的性质,b的绝对值大小反映了x 影响y 的程度;![]() 叫做回归估计值,是当x在其研究范围内取某一个值时,y值平均数
叫做回归估计值,是当x在其研究范围内取某一个值时,y值平均数![]() 的估计值。
的估计值。
回归方程的基本性质:
1、![]() 最小
最小
2、![]() =0
=0
3、直线通过(![]() ,
,![]() )
)
转化后得到回归方程的另一种形式(中心化形式):
![]()
在实际计算时,可采用以下公式:

例8.2 对大白鼠从出生第6天起,每三天称一次体重,直到第18天。数据见表8-2。试计算日龄X与体重Y之间的回归方程。
表8-2 大白鼠6-18日龄的体重
序号 |
1 |
2 |
3 |
4 |
5 |
日龄xi |
6 |
9 |
12 |
15 |
18 |
体重yi |
11 |
16.5 |
22 |
26 |
29 |
解:把数据代入上述公式,得:
![]()
![]()
![]()
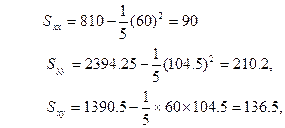
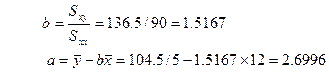
即:所求的回归方程为:y = 2.6996 + 1.5167 x
带有统计功能的计算器,只需把数据依次输入,然后按一下键就可得到上述结果。
根据直线回归方程可作回归直线,并不是所有的散点都恰好落在回归直线![]() 上,说明用此回归模型去估计y是有偏差的。
上,说明用此回归模型去估计y是有偏差的。
二、直线回归的偏离度估计
偏差平方和![]() 的大小表示了实测点与回归直线偏离的程度,因而偏差平方和又称为离回归平方和。统计学已经证明:在直线回归分析中离回归平方和的自由度为n-2。于是可求得离回归均方为:
的大小表示了实测点与回归直线偏离的程度,因而偏差平方和又称为离回归平方和。统计学已经证明:在直线回归分析中离回归平方和的自由度为n-2。于是可求得离回归均方为:![]() ,离回归均方是模型中σ2的估计值。
,离回归均方是模型中σ2的估计值。
离回归均方的平方根叫离回归标准误,记为![]() ,即
,即
![]()
Syx的大小表示了回归直线与实测点偏差的程度,即回归估测值![]() 与实际观测值y偏差的程度,于是把离回归标准误
与实际观测值y偏差的程度,于是把离回归标准误![]() 用来表示回归方程的偏离度。
用来表示回归方程的偏离度。
以后将证明:
![]()
利用此式先计算出![]() ,然后再求
,然后再求![]() 。
。
三、直线回归的显著性检验
x和y变量间即使不存在直线关系,但由n对观测值(![]() ,
,![]() )也可以根据上面的方法求得一个回归方程。显然,这样的回归方程所反应的两个变量间的直线关系是不真实的。需要判断直线回归方程的真实性。
)也可以根据上面的方法求得一个回归方程。显然,这样的回归方程所反应的两个变量间的直线关系是不真实的。需要判断直线回归方程的真实性。
先探讨依变量y的变异,然后再作出统计推断。
1.直线回归的变异来源
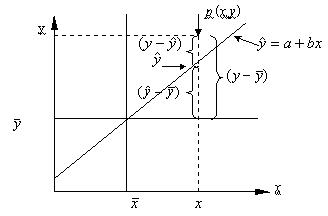
图8-1 ![]() 的分解图
的分解图
2.一元回归的方差分析
(1)无重复的情况
y的总校正平方和可进行如下的分解:
![]()
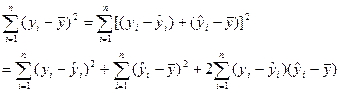
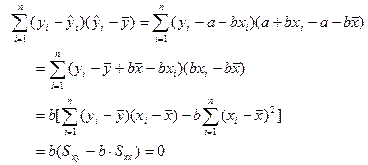
![]()
即:![]() =
=![]() +
+![]()
y的总校正平方和 残差平方和 回归平方和
自由度: ![]()
![]() 1
1
![]() 反映了y的总变异程度,称为y的总平方和,记为
反映了y的总变异程度,称为y的总平方和,记为![]() ;
;
![]() 反映了由于y与x间存在直线关系所引起的y的变异程度,称为回归平方和,记为
反映了由于y与x间存在直线关系所引起的y的变异程度,称为回归平方和,记为![]() ;
;
![]() 反映了除y与x存在直线关系以外的原因,包括随机误差所引起的y的变异程度,称为离回归平方和或剩余平方和,记为
反映了除y与x存在直线关系以外的原因,包括随机误差所引起的y的变异程度,称为离回归平方和或剩余平方和,记为![]() 。
。
把y的总校正平方和分解成了残差平方和与回归平方和。MSe可作为总体方差s2的估计量,而MSR可作为回归效果好坏的评价。如果MSR仅由随机误差造成的话,说明回归失败,X和Y没有线性关系;否则它应显著偏大。因此可用统计量
![]() (8-10)
(8-10)
对![]() 进行检验。若F < Fa(1, n-2),则接受
进行检验。若F < Fa(1, n-2),则接受![]() ,否则拒绝。
,否则拒绝。
简化公式:![]()
![]()
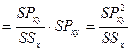
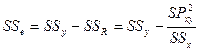
对例8.2作方差分析
解:由以前计算结果
SSy = 210.2,df = 4;SSe = 3.1704,df = 3,
SSR = 210.2−3.1704 = 207.03,df = 1
![]()
查表得F0.95(1, 3) =10.13,F0.99(1, 3) =34.12
F > F0.99(1, 3),拒绝![]() ,差异极显著,即应认为回归方程有效。
,差异极显著,即应认为回归方程有效。
(2)有重复的情况
设在每一个xi取值上对Y作了m次观察,结果记为yi1, yi2, ……yim, 则线性统计模型变为:
![]() , i = 1, 2, … n, j = 1, 2, … m
, i = 1, 2, … n, j = 1, 2, … m
估计值仍为:![]()
现在y的总校正平方和可分解为:
![]()
其中SSLOF称为失拟平方和,SSpe为纯误差平方和,表达式和自由度分别为:
![]()
![]()
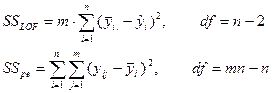
可试证明上述分解中的三个交叉项均为0。
统计检验步骤为:
I. 令![]() ,它服从F(n-2, mn-n)
,它服从F(n-2, mn-n)
若F检验差异显著,则可能的原因有:
(1)除X以外还有其他变量影响Y的取值,而统计时没有加以考虑;
(2)模型不当,即X与Y之间不是线性关系;
此时无必要再进一步对MSR作检验,而应想办法找出原因,并把它消除后重作回归。
若差异不显著,则把MSLOF和MSpe合并,再对MSR作检验:
II.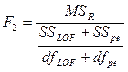 ,它服从F(1, mn-2)
,它服从F(1, mn-2)
若差异显著,说明回归是成功的,X、Y间确有线性关系;若差异仍不显著,则回归失败,其可能的原因为:
(1)X,Y无线性关系;
(2)误差过大,掩盖了X、Y间的线性关系。
如有必要,可设法减小实验误差,或增加重复数重做实验后再重新回归。
3.一元回归的t检验
由于MSe的自由度为n-2,因此上述两方差的自由度也均为n-2。有了a和b的方差与均值,我们就可构造统计量对它们进行检验:
![]()
![]() (双侧检验)
(双侧检验)
或:![]() (或
(或![]() )(单侧检验)
)(单侧检验)
统计量: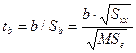
其中,![]() 为回归系数标准误。
为回归系数标准误。
当![]() 成立时,ta ~ t(n-2),可查相应分位数表进行检验。
成立时,ta ~ t(n-2),可查相应分位数表进行检验。
对例8.2中的b作t检验:
![]()
解:
![]()
![]()
![]()
![]()
查表,t0.995(3) = 5.841< t,差异极显著,应拒绝![]() ,即
,即![]() ,或X与Y有着极显著的线性关系。
,或X与Y有着极显著的线性关系。
上述统计量还有一个用途:进行两个回归方程间的比较。即检验![]() 和
和![]() 。如果两
。如果两![]() 均被接受,则可认为两组数据是抽自同一总体,从而可将两回归方程合并,得到一个更精确的方程。
均被接受,则可认为两组数据是抽自同一总体,从而可将两回归方程合并,得到一个更精确的方程。
例8.3 两组实验数据如下:
x1 |
91 |
93 |
94 |
96 |
98 |
102 |
105 |
108 |
y1 |
66 |
68 |
69 |
71 |
73 |
78 |
82 |
85 |
x2 |
80 |
82 |
85 |
87 |
89 |
91 |
95 |
y2 |
55 |
57 |
60 |
62 |
64 |
67 |
71 |
是否可从它们得到统一的回归方程?
解:从原始数据计算可得:
组别 |
n |
|
|
Sxx |
Syy |
Sxy |
MSe |
b |
a |
1 |
8 |
98.375 |
74.0 |
257.875 |
336.0 |
294.0 |
0.1357 |
1.140 |
-38.15 |
2 |
7 |
87.0 |
62.286 |
162.0 |
187.429 |
174.0 |
0.1080 |
1.074 |
-31.15 |
(1)首先检验总体方差是否相等:
![]()
![]()
查表,F0.975(6, 5) =6.978 > F,接受![]() ,可认为两总体方差相等。
,可认为两总体方差相等。
计算公共的总体方差:
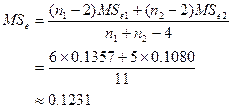
(2)检验回归系数![]() 与
与![]() 是否相等:
是否相等:![]() ;
;![]()
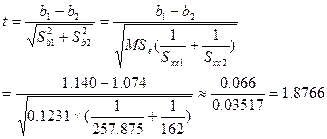
查表,得t0.975(11) = 2.201> t,接受![]() ,可认为两回归系数相等。
,可认为两回归系数相等。
共同总体回归系数的估计值为:
![]()
(3)再检验a1,a2是否相等:![]()
![]()
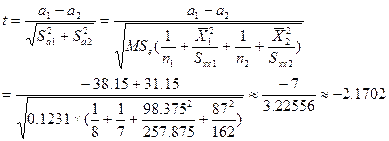
查表,t0.975(11) = 2.201,![]() ,接受
,接受![]() ,可认为:a1 = a2。
,可认为:a1 = a2。
若检验结果为a1¹a2,此题即可结束;但若检验结果为a1 = a2,则需把全部原始数据放在一起,重新进行回归:
Sxx = 902.9333,Sxy = 965.4667,Syy = 1035.7333,![]() = 93.067,
= 93.067,![]() = 68.533
= 68.533
b =![]() = 1.0693,
= 1.0693,
a=![]() = −30.9787
= −30.9787
从而得到合并的回归方程![]() 。
。
现在证明t检验与前述的F检验是一致的:
前已证明:![]() ,
,
![]() ,
,
![]()
![]()
4.点估计与区间估计
前边已经证明a和b是![]() 和
和![]() 的点估计;但作为预测值仅给出点估计是不够的,一般要求给出区间估计,即给出置信区间。
的点估计;但作为预测值仅给出点估计是不够的,一般要求给出区间估计,即给出置信区间。
![]() 和
和![]() 的区间估计
的区间估计
已经证明a和b是![]() 和
和![]() 的点估计,并求出了它们的方差。因此给出置信区间就很容易了:
的点估计,并求出了它们的方差。因此给出置信区间就很容易了:
![]()
所以![]() 的95%置信区间为:
的95%置信区间为:
![]() (8-11)
(8-11)
同理
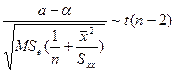
所以![]() 的95%置信区间为:
的95%置信区间为:
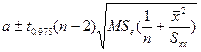 (8-12)
(8-12)
这与以前假设检验中的置信区间求法完全一样。若置信水平为99%,把分位数相应换为t0.995(n-2)即可。
对例8.2中的a和b给出95%置信区间。
解:从前边的计算可知:
a = 2.6996,b = 1.5167,Sxx = 90,MSe = 1.0568,n = 5,![]()
查表,得t0.975(3) = 3.182
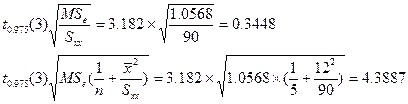
所以a的95%置信区间为:
2.6996 ± 4.3887,即(-1.6891,7.0883)
b的95%置信区间为:
1.5167±0.3448,即(1.1719,1.8615)


