第三节 回归分析的性质 

一、“回归”一词的现代含义

回归这个词首先由生物学家高尔顿（FrancisGalton）介绍。高尔顿在研究人类身高的遗传特性时发现了他所谓的“回归平均”现象。虽然父母有高的客观倾向，他们的孩子高，父母矮，孩子矮，但鉴于父母的高度，他们的孩子的平均身高倾向于“返回”到整个人口的平均身高。换句话说，虽然父母双方都非常高或异常矮小，但他们的孩子的身高往往趋向于总体平均身高。高尔顿的一般回归法也得到另一位统计学家皮尔逊（Karl Pearson）的证实。高尔顿的兴趣在于找出人口高度稳定的原因。这是“返回”一词的最初含义。

然而，对于“回归”一词的现代解释与原始意义完全不同，其现代意义是回归分析，以研究一个解释变量与另一个或多个解释变量之间的变量依赖关系，这种关系旨在估计或预测（总）平均值乘以后者的已知值或设定值（在重复采样中）。

例如，对父母身高与子女身高之间关系的研究表明，对于每个父母的身高，有一个假想的总体高度分布，对应于父亲身高的后代平均身高增加。如果你在父亲的身高和你儿子的平均身高之间画出一个一一的对应关系，你可以得到一条直线，这就是所谓的回归线，它显示了孩子的平均身高如何随着父亲的身高而变化。从现代回归的角度来看，人们关心如何找到某个父亲身高的孩子的平均身高。换句话说，人们一旦知道父母的身高，就会担心如何估计子女的平均身高。

二、回归与因果关系

回归分析研究大量变量对一个或一些变量的依赖性，但它没有揭示和解释这些变量之间是否存在因果关系。这些变量所代表的事物之间存在因果关系，因果关系的概念必须来自统计学，正如研究这些事物的实质科学所揭示的那样。回归分析可以给实证科学揭示的因果关系提供经验证据。

例如，父亲的身高和儿子的身高，我们没有任何统计理由认为我们的父亲不依赖于他们的身高，并且人们处理身高依赖于父母身高的原因是一个统计考虑因素，而常识告诉我们，我们不能把这种关系颠倒过来。从统计的角度来看，处理生成高度作为解释变量和父亲的身高作为解释变量返回，可能是一个强大的统计关系，但不能得到合理的解释，也不能得出儿子的身高父亲是荒谬结论高度的原因。也就是说，在逻辑上，统计公式本身并不表示任何因果关系。事物之间的因果关系必须依靠超验或理论思考或启示。

三、回归分析与相关分析

尽管与回归密切相关，但测量两个变量之间线性相关性主要目的的相关分析在概念上有很大不同。相关系数用来衡量可变（线性）指数的相对程度。实际上，也许我们对作物产量和降雨量，人体高度和体重，吸烟时间和肺癌发病率之间的相关性感兴趣，并计算它们的相关系数。然而，在回归分析中，我们对这个度量没有兴趣，并且有兴趣根据其他变量的设定值来估计或预测变量的平均值。

回归和相关分析之间存在一些基本差异。在回归分析中，解释变量和解释变量的处理方法存在不对称性。解释变量是具有概率分布的随机变量，而解释变量不是随机的，固定值取自重复采样。但在相关分析中，我们对称地对待任何（两个）变量，两个变量被认为是随机的，解释变量和解释变量之间没有区别，大多数相关理论都是基于变量的随机假设。大多数回归理论是基于假设解释变量是随机的，解释变量是随机的。因此，根据理论分析，相同的两个变量可以拟合两个不同的回归方程，但只能计算相关系数。例如，我们可以将人的身高作为解释变量，以人体重量作为解释变量的回归模型，或者将人体重量解释为变量的回归模型，而人的身高是以相关系数计算。

相关分析和回归分析之间也有一些基本的联系。一般来说，在回归分析之前，有必要分析相关变量（定性和定量分析）并在进一步回归分析之前确定相关关系。因此，可以说相关分析是回归的前提条件，回归分析是相关性的深化。

在X和Y均为随机变量的情况下，通常可以X为自变量，Y为因变量建立方程，也可反过来，以Y为自变量，X为因变量建立方程。此时它们的地位是对称的。

取X为自变量，Y为因变量，回归系b为：

取Y为自变量，X为因变量，回归系数b’为：

因为

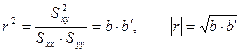
即：相关系数实际是两个回归系数的几何平均值。这正反映了相关与回归的不同：相关是双向的关系，而回归是单向的。

三种对回归方程统计检验的的比较：

（1）对一元线性回归来说，它们的基本公式其实是等价的，因此结果也是一致的。

（2）各有优缺点：对b的t检验可给出置信区间；方差分析在有重复的情况下可分解出纯误差平方和，从而可得到进一步的信息；相关系数则既直观，又方便（有专门表格可查），因此使用广泛。

需注意，不论采用什么检验方法，数据都应满足以下三个条件：独立，抽自正态总体，方差齐性。

四、“线性”一词的含义

描述统计关系的回归模型在数学形式上有线性和非线性之分。但是，在回归分析中，“线性”一词的含义可作两种解释。

对线性的第一种解释也许是更“自然”的解释是，的条件期望是的线性函数。从几何意义上说，这时回归曲线是一条直线。按照这种解释，诸如，等，就不是线性函数。

对于线性的第2种解释是，的条件期望是诸参数、的线性函数；它可以是也可以不是变量的线性函数。对于这种解释，和都是线性回归模型，而则不是，后者（对参数而言）是非线性回归模型的一个例子。

在两种线性的解释中，对于我们即将展开讨论的回归理论来说，主要考虑的是对参数为线性的情形，也就是说，从现在起，“线性”回归一词总是指对参数为线性的一种回归，即参数总是以它的一次方出现。对解释变量则可以是也可以不是线性的。划分的标准是回归模型的条件期望关于参数的导数是否与参数有关，即期望函数关于参数的一阶导函数是否仍然是参数的函数。若不是，则称该回归模型是线性回归函数，若是，则称为非线性回归函数。