第八章 相关与回归分析

学习要求：  通过对实际问题的分析，了解回归分析的必要性与回归分析的一般步骤；了解线性回归模型与函数模型的区别；尝试做散点图，求回归直线方程；能用所学的知识对实际问题进行回归分析，体会回归分析的实际价值与基本思想。

前面章节讨论的问题都只涉及一个变量，但由于客观事物在发展过程中是相互关联和相互作用的，因此经常有必要研究生物测试研究中两个或两个以上变量之间的关系。如果研究温度与作物生长速度之间的关系，则温度与发育进程有两个变量；研究每亩穗数，每穗粒数和亩产量的关系，有穗数，粒数和产量三个变量。变量之间有两种类型的关系，一种是完全确定性变量之间的关系，可以用精确的数学表达式表示，如矩形区域（S）和长度（a）和宽度（b）可以表示为：S= ab。它们之间的关系是确定性的，只要知道两个变量的值可以准确地计算出另一个变量的值，这种变量之间的关系就称为函数关系。二是变量之间没有完全确定的关系，不能用精确的数学公式表示，如身高与体重的关系，仔猪出生体重与断奶体重的关系，瘦肉率与背部脂肪厚度，眼肌面积，胴体长度等等，这些变量彼此密切相关，但是另一个变量的值不能通过一个或几个变量的值精确计算。

相关变量之间的关系一般分为两种，一种是因果关系，即一个变量受另一个或多个变量的影响，如受遗传因素影响的仔猪生长率，营养，饲养管理因素，身高他们的孩子受父母的高度影响；另一种是平行关系，也就是说，两个以上的变量都受到其他因素的影响，比如身高与体重的关系，兄弟身高的关系是一种平行关系。

变量与分析方法之间的关系总结如下：

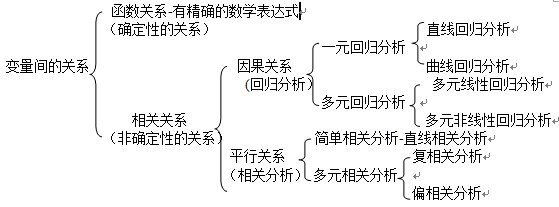
 第一节  变量之间的相互关系 

一、相关程度与方向

从某种意义上说，函数关系是关系的一个特例，也就是说，变量之间的严格逐一对应关系是最相关的关系，称为完全关联（perfectassociation）。变量相关程度的另一个极端值是无相关性（noassociation）或0相关性（zero association），即变量之间没有量化依赖关系。两个极值之间的相关性并不完全相关，大多数相关性指的是这种情况，那么变量之间存在定量关系并不是非常严格的相互依赖性。

在统计中，对于线性相关，采用相关系数（记作r）这一指标来量度相关关系程度或强度。就线性相关来说，当＝l时，表示为完全相关；当r=0时，表现为无相关或零相关；当0<<1时，表现为不完全相关。但在采用相关系数r这一指标时必须注意到，存在着完善曲线而r＝0的情况。当然，变量在其他测量层次的关系强度，也可以用同样的思路加以考虑。

当变量有关时，我们也可以探索它们的相关方向，可以分为正向和负向两个方向。正相关是当一个变量的值增加而另一个变量的值增加时。负相关性是一个变量的值增加而另一个变量的值减小，以强调只有高于该顺序的测量级别的变量才能分析相关方向，因为只有这些变量的值具有高或一个低或几个点。对于固定类变量，由于变量的值不是大小，点的高度，所以与其他变量相关的固定类变量没有正方向或负方向。

二、因果关系

除了这两个属性的相关性和方向之外，我们还应该注意这两个变量之间的关系是因果关系。只有当两个变量之间的关系满足以下三个条件时，该关系才具有因果关系：

（1）两个变量有一个公共变量，即一个变量的变化会伴随另一个变量的变化。

（2）两变量之间的关系不是由其他因素形成的，即变量的变化是由自变量的变化引起的。

（3）两个变量的生成和变化具有确定的时间顺序，即一个在前面，另一个在后面，前者称为参数，另一个是因变量。

因果关系是一种不对称关系（asymmetricalrelationship），此时只有自变量影响因变量，因为变量不会影响自变量。这被称为对称关系（symmetricalrelationship）如果变量的作用方向不能确定或区分。

三、相关关系的种类

现象之间的相关性可以通过不同的符号来区分。

根据相关度分为：

（1）完全相关：现象数量的变化完全由其他现象的数量决定；

（2）不相关：两种现象互不影响，其数量独立变化；

（3）不完全相关：这两种现象之间的关系是完全相关和不相关的。这是一个关联主题。

在相关的方向上：

（1）正相关：当一个现象的数量从小到大时，其他现象的数量也相应从小到大；

（2）负相关：当现象的数量变小时，其他现象的数量变小。

按相关的形式分为：

（1）线性相关性：两种相关现象之间的关系大致呈线性关系；

（2）非线性相关性：两种相关现象之间的关系近似表示为曲线。

按影响因素的多少分为：

（1）单相关（也称简单相关）：两个变量之间的关系；

（2）复相关（多元相关）：三个或三个变量之间的关系，即两个或两个以上自变量的因变量；

（3）偏相关：一种与各种情况有关的现象，当其他变量被假定为相同时，其中与关系相关的两个变量称为偏相关。例如，在人们收入水平不变的假设下，商品需求与其价格水平之间的关系是偏相关的。

四、相关和回归分析的任务

相关和回归分析是研究现象之间相关性的两种基本方法。

所谓的相关性分析（相关性）是显示现象之间相互依存程度密切程度的指标。

所谓回归分析（回归）就是根据相关关系的具体形式选择一个合适的数学模型来表示变量之间的平均变化关系。

相关和回归分析的任务是：

（1）确定这种现象与这种关系的出现之间是否存在关系。这是相关分析的前提。

（2）确定亲密关系的程度。相关分析的目的之一就是从较不严谨的关系中判断关系的紧密程度。

（3）确定关系的数学模型。

（4）确定变量的估计值的误差程度。

估计值与实际值之间存在差异，并且估计该变量的估计值的误差度的指标。估计的标准是错误的，估计不准确，估计的标准很小，这表明估计更准确。