第四节 R软件的应用 

一、ANCOVA

协方差分析（ANCOVA）模型包括连续变量X（称为协变量），其通常与因变量相关。

               （7-12）

在任何实验操作之前，协变量的值通常被收集或可用。这确保了协变量的值独立于实验因素。如果它们不是独立的，ANCOVA的逻辑就会崩溃。

在模型中包含一个协变量会产生两个理想的效果：

1.误差项（公式7-12中的）减少，从而产生更强大的统计测试。从误差项中删除可以由协变量分数考虑的因变量方差。

2.协变量和因变量之间关系的斜率估计（在上面的公式7-12中）允许您在因变量上进行数值调整得分，并询问（通常有用的）问题：如果这些群体在协变量上是相等的，那么它们是因变量吗，得分是多少？

为了评估治疗因素的影响，我们将比较以下限制型和完整型：

全模型：

                （7-13）

限制模型：

                   （7-14）

注意协变量如何在两个模型中出现。我们问：在我们去除协变量所解释的方差之后，是否存在治疗因素的影响（是参数为零）？

还要注意整个模型（7-12）的方程式中，和参数分别可以看作是将协变量X与因变量Y相关的直线的截距和斜率。我们来看看这个图形。

想象一下，我们有来自10名受试者的数据，两组中的每组5名（例如对照组和实验组）。我们对因变量Y有分数，对于每个主题，我们也有对协变量X的得分。比方说，为了举例说明，我们正在测试一种新药是否有助于提高记忆力。这两组是安慰剂和药物，因变量是在记忆测试中回想的项目数量。比方说，我们从以前的研究中知道智商分数是预测性的（与记忆相关），所以我们对每个10个科目都有智商分数。

我们可以用特定的方式绘制数据来说明ANCOVA的原理。我们将为每个主题绘制一个点，其纵轴上的因变量得分，横轴是协变量的得分，我们将使用不同的符号来表示安慰剂组与药物组的成员身份。

       > memoryscore <- c(7.0, 7.7, 5.4,10.0, 11.7, 11.0, 9.4, 14.8, 17.5, 16.3)

> group <-factor(c(rep("placebo", 5), rep("drug", 5)),

+levels=c("placebo", "drug"))

> iq <-c(112,111,105,115,119,116,112,121,118,123)

>plot(iq,memoryscore,pch=c(rep(1,5),rep(24,5)),bg=c(rep(1,5),rep(21,5)))

>legend("topleft", c("placebo","drug"),pch=c(1,24), pt.bg=c(1,21))  

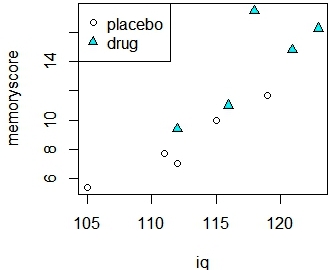
图7-1 新药与记忆力关系图 

我们可以看到三件重要的事情：

1.因变量上的群体之间似乎有区别。平均记忆评分为8.4，安慰剂组为13.8。

2.记忆得分和智商之间显然存在线性关系。

这两个团体的智商分数似乎也不一样。安慰剂组的平均智商为112.4，而药物组为118。

如果我们用简单方差分析来比较两个组，忽略协变量，

我们会得到以下结果：

> options(contrasts =c("contr.sum", "contr.poly"))

> mod.1 <-lm(memoryscore ~ group)

> a <-anova(mod.1)

> pval.1 <-a$`Pr(>F)`[1]

> mse.1 <- a$`MeanSq`[2]

> print(a)

Analysis of VarianceTable

Response: memoryscore

          Df Sum Sq Mean Sq F value  Pr(>F) 

group      1 73.984 73.984  8.1043 0.02158 *

Residuals  8 73.032  9.129                  

---

Signif.codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05‘.’ 0.1 ‘ ’ 1

我们会看到，组效应的综合检验在0.05水平显著（p = 0.022）。记下组内差异。我们可以看到ANOVA输出中的误差项（残差的平均值）是9.129。

我们可以用这种方式来想象它：水平线是每组的平均记忆分数。垂直虚线表示整个模型下的错误。

>plot(iq,memoryscore,pch=c(rep(1,5),rep(24,5)),bg=c(rep(1,5),rep("red",5)))

>legend("topleft", c("placebo","drug"),pch=c(1,24), pt.bg=c(1,"red"))

> for (j in 1:2) {

 if (j==1) {

w <- c(1,2,3,4,5)

cl <- 1

 }

if (j==2) {

w <- c(6,7,8,9,10)

cl <- "red"

 }

 lines(c(min(iq[w]),max(iq[w])),c(mean(memoryscore[w]),

mean(memoryscore[w])),col=cl)

for (i in 1:length(w)) {

lines(c(iq[w[i]],iq[w[i]]),c(memoryscore[w[i]],

mean(memoryscore[w])),lty=2, col=cl)

                   }

}

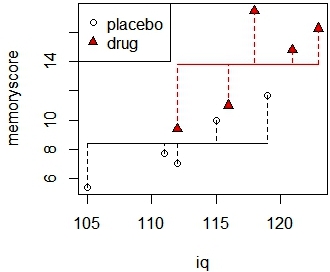
图7-2 不同组间记忆力得分差异 

       然后，ANCOVA的想法是解释或表示记忆分数的变化，这种变化可以通过IQ变化来捕捉。这是通过将记忆分数和智商之间的关系建模为一条直线来完成的。我们可以用下面的方式运行ANCOVA（见下面的代码），因为我们可以使用lm（）函数明确地将完整和受限模型表示为线性模型，然后使用lm（）函数执行F检验 anova（）函数来比较每个模型。我也在下面显示，你也可以在整个模型上单独使用anova（）函数。

> mod.full <-lm(memoryscore ~ iq + group)

> mod.rest <-lm(memoryscore ~ iq)

> a2 <-anova(mod.full, mod.rest)

> print(a2)

方差分析表

Model 1: memoryscore ~iq + group

Model 2: memoryscore ~iq

Res.Df RSS Df Sum of SqF Pr(>F)

1 7 20.913

2 8 31.273 -1 -10.36 3.4678 0.1049

> a3 <-anova(mod.full)

> print(a3)

方差分析表

Response:memoryscore

DfSum Sq Mean Sq F value Pr(>F)

iq1 115.743 115.743 38.7412 0.0004349 ***

group1 10.360 10.360 3.4678 0.1048703

Residuals7 20.913 2.988

---

Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

>pval.2 <- a3$`Pr(>F)`[2]

>mse.2 <- a3$`Mean Sq`[3]

注意我们的误差项（平均残差= 2.988）低于我们运行方差分析时没有协变量的程度。另外请注意，组效应不再显著！对于组的影响的测试，p = 0.105。

在图形上，我们可以通过绘制每组对应每对（，）的线来表示ANCOVA全模型。记住是截距，是（普通）斜率。

>plot(iq,memoryscore,pch=c(rep(1,5),rep(24,5)),bg=c(rep(1,5),rep("red",5)))

>legend("topleft", c("placebo","drug"),pch=c(1,24), pt.bg=c(1,"red"))

> mod.full.coef <-coef(mod.full)

>print(mod.full.coef)

(Intercept) iq group1

-50.7033113 0.5363135-1.2183223

> placebo.pred <-predict(mod.full)

> for (j in 1:2) {

if (j==1) {

     w<- c(1,2,3,4,5)

cl <- 1

}

if (j==2) {

w <- c(6,7,8,9,10)

cl <- "red"

}

lines(c(min(iq[w]),max(iq[w])),

c(min(placebo.pred[w]),max(placebo.pred[w])), col=cl)

}

}   

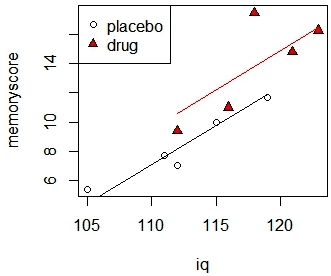
图7-3 每组对应每对（，）图（一）  

coef（）函数为我们提供了mod.full的模型系数，这是我们的完整模型（应用于上面完整模型公式的lm（）函数的输出）。IQ值（0.536）是上述公式中线条斜率的估计值。截距值（-50.703）是的值，即组因子的第一级的截距，即安慰剂。这是棘手的，并且是一个R gotcha：group1的值（-1.218）不等于，但是你必须添加到以便估计。因此= -50.703 + 0.536 = -50.167。

现在，对组的影响进行测试，基本上是对包含截距的完全模型的测试，，对于组因子（安慰剂，药物）的每一个级别来说都是一个明显好于仅包含一个截距的限制性模型（在这种情况下，因为模型中缺少了，所以截距是简单的并且由于它没有下标j，因此对于组因子的每个级别都是相同的）。

在上面的例子中，与完整模型相对应的两条线的截距（和的值）彼此足够相似，以至于限制模型可能同样适用于数据（事实上，根据我们上面执行的F检验）。

>plot(iq,memoryscore,pch=c(rep(1,5),rep(24,5)),bg=c(rep(1,5),rep("red",5)))

>legend("topleft", c("placebo","drug"),pch=c(1,24), pt.bg=c(1,"red"))

> for (j in 1:2) {

if (j==1) {

w <- c(1,2,3,4,5)

cl <- 1

}

if (j==2) {

w <- c(6,7,8,9,10)

cl <- "red"

}

lines(c(min(iq[w]),max(iq[w])),

c(min(placebo.pred[w]),max(placebo.pred[w])), col=cl)

for (i in 1:length(w)) {

lines(c(iq[w[i]],iq[w[i]]),

c(memoryscore[w[i]],placebo.pred[w[i]]), lty=2, col=cl)     

 }

}

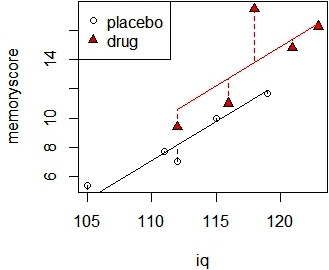
图7-4 每组对应每对（，）图（二）

二、调整平均数

       运用ANCOVA并估计了智商与记忆成绩之间的关系后，我们现在可以回答一个有趣的问题：如果他们的智商得分相似，安慰剂组和药物组的记忆成绩是多少？当然，他们在智商上的得分并不相似，但ANCOVA允许我们回答这个问题，如果他们是相似的，然后考虑我们知道记忆得分如何随着智商而变化（独立于任何实验操作，如安慰剂对药物），他们的分数会是多少？

我们将要求R根据包含和参数的完整模型生成记忆得分的预测值。如果安慰剂组和药物组的智商得分相同，我们将要求R产生对于记忆得分的预测。我们将不得不选择一些任意的智商值，通常是在两组中选择智商的平均值。我们将使用predict（）命令从我们的完整模型中生成预测。

       > group.predict <-factor(c("placebo","drug"), levels=c("placebo","drug"))

> iq.predict <-rep(mean(iq), 2)

> data.predict <-data.frame(group=group.predict, iq=iq.predict)

> print(data.predict)

group iq

1 placebo 115.2

2 drug 115.2

> adjmeans <-predict(mod.full, data.predict)

> data.predict =data.frame(data.predict, memoryscore=adjmeans)

> print(data.predict)

group iq memoryscore

1 placebo 115.2 9.861678

2 drug 115.2 12.298322

       所以我们看到，我们的完整模型预测，如果安慰剂组和药物组在智商上相同（对于这两个组，智商= 115.2），那么安慰剂组的平均记忆分数将是9.86，并且药物组将一直是12.3。将其与原始未调整的平均值（安慰剂= 8.36和药物= 13.8）相比较，你会发现在这种情况下，通过算术调整IQ的群体差异，导致记忆得分差异更小。

以图形方式，我们可以通过在IQ = 115.2处绘制垂直线并确定为每个组截取该线的记忆值的值来了解预测的工作方式。

       >plot(iq,memoryscore,pch=c(rep(1,5),rep(24,5)),bg=c(rep(1,5),rep("red",5)))

>legend("topleft", c("placebo","drug"),pch=c(1,24), pt.bg=c(1,"red"))

> for (j in 1:2) {

if (j==1) {

w <- c(1,2,3,4,5)

cl <- 1

}

if (j==2) {

w <- c(6,7,8,9,10)

cl <- "red"

}

lines(c(min(iq[w]),max(iq[w])),

c(min(placebo.pred[w]),max(placebo.pred[w])), col=cl)

abline(v=mean(iq),lty=3, col="blue")

abline(h=adjmeans[1],lty=2, col="black")

abline(h=adjmeans[2],lty=2, col="red")

}   

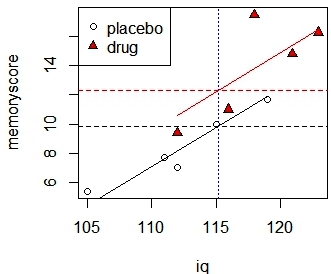
图7-5 每组对应每对（，）图（三） 

通过包含一个协变量，你可以用很多方式改变你的结论（或者根本不能改变它们）。一个显而易见的影响可能会变得更弱，或者逆转，或者完全被忽视。效应可以变得更强大。考虑一下你的数据集中必须存在的条件，以便发生这些不同类型的场景。

三、ANCOVA假设

ANCOVA假设因变量的得分必须是正态分布的，并且它们必须在协变量的所有值处都是如此。

回归假设的同质性是因变量和协变量之间的关系的斜率对于所有组是相同的。在我们完整模型的等式中，由于没有下标（表示每个组的不同值，即该因子的每个等级），所以这是显而易见的。

话虽如此，没有任何东西可以阻止您为每个组配备不同斜率的完整模型。它看起来像这样：

代价是，你必须估计每一个额外的斜率，你会失去一定程度的自由度。此外，它提出了一个棘手的问题，为什么不同群体在因变量和协变量之间有不同的关系？这可能不是问题。然后再次它可能是。这取决于情况和因变量，协变量和实验设计的含义。通过比较，您可以非常容易地进行测试，以查看斜坡是否不同以下两种模式：

全模型：

约束模型：

在R中，您可以简单地将包含交互术语的模型与不包含交互术语的模型进行比较。换句话说，在完整模型中，记忆分数（斜率）上的智商效应取决于组的水平（这是交互的定义）。在受限制的模式中，它没有此项。

       > mod.F <- lm(memoryscore ~ iq +group + iq:group)

> mod.R <-lm(memoryscore ~ iq + group)

> anova(mod.F, mod.R)

    Analysis of Variance Table

Model 1: memoryscore ~iq + group + iq:group

Model 2: memoryscore ~iq + group

Res.Df RSS Df Sum of SqF Pr(>F)

1 6 19.519

2 7 20.913 -1 -1.3943 0.4286 0.537

或者我们可以简单地列出完整模型的anova表格：

> anova(mod.F)

Analysis of VarianceTable

Response: memoryscore

Df Sum Sq Mean Sq Fvalue Pr(>F)

iq 1 115.743 115.74335.5788 0.0009948 ***

group 1 10.360 10.3603.1848 0.1245828

iq:group 1 1.394 1.3940.4286 0.5369540

Residuals 6 19.519 3.253

---

Signif.codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

       调整均值的含义是什么？

虽然ANCOVA允许你用算术调整分数来预测他们在协变量上是否相等时的情况，但如果事实上在你的实验中它们在协变量上不相等，那么它可能很难解释调整后的分数，特别是当您的实验涉及某种治疗时。例如，在我们在这里提供的关于记忆，药物与安慰剂和智商的假数据中，如果所讨论的药物对智商低的人的记忆力实际上有不同的影响，那么高智商的人会如何？要真正解决这个问题，唯一的方法就是在治疗前先将协变量的受试者等同于第一位。您也可以考虑将您的协变量转化为一个真正的因素（例如，将您的设计与智商水平交叉，例如低，中，高）。

跟踪测试平均值

在对ANCOVA进行综合测试后，您可能希望对个别方式进行后续测试。测试是在调整后的手段上完成的。不幸的是，没有按钮也没有一个简单的R命令在ANCOVA之后执行后续测试。进行后续测试的一种方式，并且在很多方面最灵活的方法是计算Maxwell＆Delaney文章中描述的F比。在精装第二版配对比较中，第435，方程37和38；以及任何任意的对比：第436页，方程39，41和42。F比率的分母不再只是作为均方误差读出ANOVA输出表，它的均方误差乘以a看起来很难看，需要计算。编写R函数来计算分母是较为简单的的事情。请注意，这些检测未针对Type-I错误进行修正。通过使用将获得的F值转换为q，然后使用和计算基于q分布的概率，其中a是组数。

下面使用一个示例表明如何具体操作：

> mydv <-c(2,3,5,4,5,6,6,8,9,7,13,15,16,17,18)

> mygroup <-c(1,1,1,1,1,2,2,2,2,2,3,3,3,3,3)

> mygroupf <-factor(mygroup)

> mycovariate <-c(10,11,13,12,10,13,14,14,13,12,18,18,21,23,22)

> rawmeans <-tapply(mydv, list(mygroupf), mean)

> print(rawmeans)

1 2 3

3.8 7.2 15.8

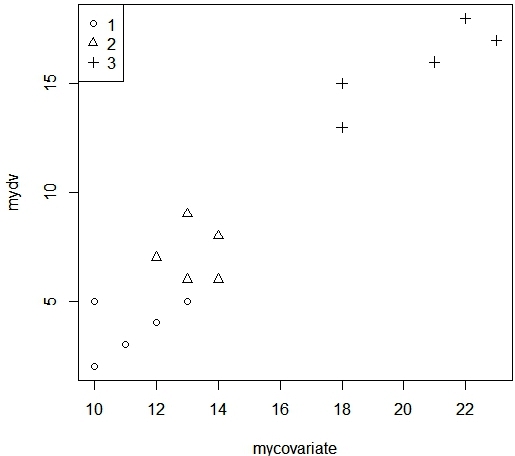
> plot(mycovariate,mydv, pch=mygroup)

>legend("topleft", legend=levels(mygroupf), pch=unique(mygroup))

 

应用ANCOVA模型：

> mymod <- lm(mydv~ mycovariate + mygroupf)

> mymod.anova <-anova(mymod)

> print(mymod.anova)

Analysis of VarianceTable

Response: mydv

Df Sum Sq Mean Sq Fvalue Pr(>F)

mycovariate 1 379.14379.14 239.5787 8.186e-09 ***

mygroupf 2 14.39 7.194.5452 0.03641 *

Residuals 11 17.41 1.58

---

Signif.codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

现在我们来计算调整后的均值。

> # generate adjustedmeans

> mygroup.predict<- factor(c(1,2,3))

> mycovariate.predict<- rep(mean(mycovariate), 3)

> mydata.predict<- data.frame(mygroupf=mygroup.predict,

mycovariate=mycovariate.predict)

>print(mydata.predict)

mygroupf mycovariate

1 1 14.93333

2 2 14.93333

3 3 14.93333

> adjmeans <-predict(mymod, mydata.predict)

> print(adjmeans)

1 2 3

6.030303 8.23549812.534199   

现在让我们做一个对比比较调整后的手段1和2。

> # compare adjustedmean 1 and adjusted mean 2

> Y1 <-adjmeans[1] # adjusted mean 1

> Y2 <- adjmeans[2]# adjusted mean 2

> a <-length(levels(mygroupf)) # total number of groups

> N <-length(mydv) # total number of subjects in whole experiment

> n <- N/a #number of subjects in each group

> mse <-mymod.anova$`Mean Sq`[3] # error term from the ANOVA output table

> n1 <- n

> n2 <- n

> # the extra junk inequation 37, Maxwell & Delaney

> i1 <-which(mygroup==1)

> i2 <-which(mygroup==2)

> i3 <-which(mygroup==3)

> sse1 <-sum((mydv[i1]-mean(mydv[i1]))^2)

> sse2 <-sum((mydv[i2]-mean(mydv[i2]))^2)

> sse3 <-sum((mydv[i3]-mean(mydv[i3]))^2)

>denom_mult <- (1/n1) + (1/n2) + (((Y1-Y2)^2)/(sse1+sse2+sse3))

> s2y1y2 <- mse *denom_mult

> dfnum <- 1

>dfdenom <- N-a-1

>Fobs <- ((Y1-Y2)^2)/s2y1y2

> p.value.uncorrected= pf(Fobs, dfnum, dfdenom, lower.tail=FALSE)

>print(p.value.uncorrected)

1

0.04062419

> qobs = sqrt(2*Fobs)

> p.value.tukey =ptukey(q=qobs, nmeans=a, df=dfdenom, lower.tail=FALSE)

>print(p.value.tukey)

1

0.09477965

另一种可能性是使用R中的multcomp包（你可以下载并安装）。它可以按照以下方式对调整均值执行成对Tukey测试。注意结果如何表示为t检验，并且与使用Maxwell和Delaney方程时的概率不完全相同。我不知道这是为什么，正在研究中。可能的原因是，glht（）的内部正在做一些与Maxwell＆Delaney所建议的不同的东西。

> library(multcomp)

>summary(glht(aov(mydv ~ mycovariate + mygroupf),linfct=mcp(mygroupf="Tukey")))

Simultaneous Tests forGeneral Linear Hypotheses

Multiple Comparisons ofMeans: Tukey Contrasts

Fit: aov(formula = mydv~ mycovariate + mygroupf)

Linear Hypotheses:

Estimate Std. Error tvalue Pr(>|t|)

2 - 1 == 0 2.2052 0.91572.408 0.0714 .

3 - 1 == 0 6.5039 2.23202.914 0.0300 *

3 - 2 == 0 4.2987 1.81572.368 0.0762 .

---

Signif. codes: 0 `***'0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

(Adjusted p valuesreported -- single-step method)