第三节 协方差分析的计算过程
本节中我们给出较详细的协方差分析计算过程,包括全部应进行的条件检验。
(1)对各处理水平,分别计算协变量与因变量的回归方程,并求出各处理内的剩余平方和![]() ,令
,令![]() ,称为组内剩余平方和,其自由度
,称为组内剩余平方和,其自由度![]() 。
。
(2)令![]() ,并利用它们检验方差齐性。可选取差异最大的两个的比值作Fmax统计检验,若无显著差异,则可认为具有方差齐性。
,并利用它们检验方差齐性。可选取差异最大的两个的比值作Fmax统计检验,若无显著差异,则可认为具有方差齐性。
(3)把各处理水平的平方和及交叉乘积和合并得到Eyy,Exx,Exy;并求得公共回归系数![]() ,及
,及![]() ,称为误差平方和,它的自由度为
,称为误差平方和,它的自由度为![]() 。
。
(4)检验各处理水平的回归线是否平行:![]() 。由于组内剩余平方和
。由于组内剩余平方和![]() 完全是由随机误差引起,而用共同的b*计算出的SSe则包含了随机误差及各水平回归系数bi的差异的影响,而且可证明它是可以分解的,所以有:
完全是由随机误差引起,而用共同的b*计算出的SSe则包含了随机误差及各水平回归系数bi的差异的影响,而且可证明它是可以分解的,所以有:
![]()
其自由度![]() ,令
,令
![]()
然后用
![]()
作检验。若差异不显著,则可认为各![]() 相等。
相等。
(5)检验回归是否显著:![]() 利用(2)的结果,
利用(2)的结果,![]() 。SSe = Eyy − SSR,
。SSe = Eyy − SSR,![]() 。令
。令![]() ,可用
,可用
![]()
对上述H0作检验。若差异显著则作协方差分析,若差异不显著则直接作单因素方差分析。
(6)协方差分析:
计算:
![]()
![]()
![]()
令
![]() ,
,
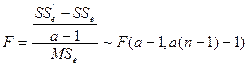
利用上述统计量F对![]() 作上单尾检验。若差异显著,则认为各处理水平间效果有显著差异。
作上单尾检验。若差异显著,则认为各处理水平间效果有显著差异。
(7)计算调整平均数![]() ,即
,即![]() 的估计值。
的估计值。
![]()
其标准差为:

必要时可用它对上述估计值间差异是否显著作检验。
协方差分析的原理及步骤(设![]() )
)
(1)检验条件:先作三条回归线,求出各组的误差估计![]() 并检验是否相等(方差齐性),通过检验后合并各
并检验是否相等(方差齐性),通过检验后合并各![]() 求出
求出![]() 为误差估计。
为误差估计。
再假设三线平行(有共同的b*),在此假设下求出SSe,用![]() 对
对![]() 检验上述假设。通过检验后用MSe代替
检验上述假设。通过检验后用MSe代替![]() 。
。
再检验b*是否为0。令![]() ;通过检验则直接作方差分析,否则做协方差分析。
;通过检验则直接作方差分析,否则做协方差分析。
(2)协方差分析:检验各水平效应是否均为0:![]() 。在此假设下,可把三组数据合并,作一个回归方程,它的剩余平方和
。在此假设下,可把三组数据合并,作一个回归方程,它的剩余平方和![]() 包含了
包含了![]() 的影响。令
的影响。令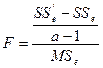 ,检验
,检验![]() 影响是否明显比随机误差大。
影响是否明显比随机误差大。
(3)对平均数进行调整,即对![]() 作出估计,必要时进行多重比较。
作出估计,必要时进行多重比较。
例7.1 比较三种猪饲料A1,A2,A3的效果。X为初始重量,Y为增重量,数据见下表。
A1 |
X |
15 13 11 12 12 16 14 17 |
|
Y |
85 83 65 76 80 91 84 90 |
| |
A2 |
X |
17 16 18 18 21 22 19 18 |
|
Y |
97 90 100 95 103 106 99 94 |
| |
A3 |
X |
22 24 20 23 25 27 30 32 |
|
Y |
89 91 83 95 100 102 105 110 |
|
解:首先进行条件的检验。
(1)对每一种饲料分别作回归分析,得:
Syy1 =487.5, Sxy1 = 110.5, Sxx1 = 31.5,
a1= 33.516, b1 = 3.506, ![]()
Syy2= 184, Sxy2 = 65, Sxx2 = 27.875,
a2= 54.570, b2 = 2.332, ![]()
Syy3= 566.875, Sxy3 = 245.375, Sxx3 = 115.875,
a3= 43.131, b3 = 2.118, ![]()
组内剩余平方和:
![]()
(2)检验方差齐性:由于各水平重复数均为8,误差自由度均为6。可选差异最大的![]() 和
和![]() 作检验:
作检验:
Fmax = 99.873 /32.431 = 3.080
由于共有3组,因此a=3;各组自由度均为6,因此v=6。查Fmax,临界值表。得:
Fmax, 0.05(3, 6)= 8.38 > Fmax,
可认为具有方差齐性。
(3)合并各水平的平方和及交叉乘积和:
Eyy= 1238.375, Exy = 420.875, Exx = 175.25
b*= Exy / Exx = 2.402, SSe= Eyy −![]() = 227.615
= 227.615
(4)检验回归线是否平行: H0 : b1 = b2 =b3 = b*
SSb = SSe −![]() = 48.038
= 48.038
![]()
查表,F0.95(2, 18)= 3.55 > F, 所以接受![]() ,可认为三回归线平行,即有公共回归系数b*。
,可认为三回归线平行,即有公共回归系数b*。
(5)检验回归是否显著:H0 :β= 0
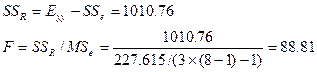
查表,F0.99(1, 20) =8.096 < F,所以差异极显著,X与Y有极显著线性关系,应作协方差分析。
(6)把所有数据放在一起,算得:
Syy= 2555.958, Sxy = 1080.75, Sxx = 720.5
(7)协方差分析:![]()
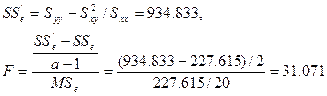
查表,F0.99(2, 20) =5.849 < F,所以拒绝H0,各不同饲料增重效果差异极显著。
(8)为比较各饲料好坏,计算调整平均数![]() :
:
![]() 。
。
代入数据,得:
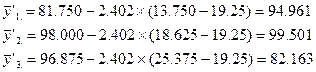
从调整后的数据来看,第二种饲料效应最好,第一种饲料效应稍差,第三种饲料效应更多。但从调整前的数据来看第二好的,第三好的数据与第二好的差不多,第一个差异很大。此调整之前的差异不正确,因为它包含初始重量效果。第三组初始体重明显较大,第一组较小,影响了两种饲料的正确评价。
如果希望对各调整后的平均数据作统计比较,可用公式![]() 计算它们的样本方差:(分别记为
计算它们的样本方差:(分别记为![]() )。
)。
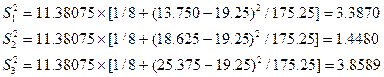
自由度均为20。
先比较![]() 和
和![]() :
:
![]()
查表,得:t0.979(20) = 2.086,t0.995(20) = 2.845
所以差异已接近显著水平,但仍未达到。故应认为第二种饲料近似地与第一种相同。
再比较![]() 和
和![]() :
:
![]()
所以差异极显著。第三种饲料极明显地差于第一种。由于第二种平均值大于第一种,方差小于第一种,故第二种与第三种的差异更大。即第三种极明显地差于其他两种。
注意由于MSe是用全部数据算出的公共的误差估计,其自由度为20,因此![]() 的子样方差为
的子样方差为
![]() ,
,
自由度仍应为20,而不是40。
例7.2 为了寻找一种较好的哺乳仔猪食欲增进剂,以增进食欲,提高断奶重,对哺乳仔猪做了以下实验:实验设对照、配方1、配方2、配方3共四个处理,重复12次,选择初始条件尽量相近的长白种母猪的哺乳仔猪48头,完全随机分为4组进行实验,结果见表7-1,试作分析。
此例,![]() =18.25+15.40+15.65+13.85=63.15
=18.25+15.40+15.65+13.85=63.15
![]() =141.80+130.10+144.80+133.80=550.50
=141.80+130.10+144.80+133.80=550.50
k=4,n=12,kn=4×12=48
表7-1 不同食欲增进剂仔猪生长情况表 (单位:kg)
处 理 |
对照 |
配方1 |
配方2 |
配方3 | ||||
观 测 指 标 |
初生重 x |
50日 龄重y |
初生重 x |
50日 龄重y |
初生重 x |
50日 龄重y |
初生重x |
50日 龄重y |
观察值 xij,yij |
1.50 12.40 |
1.35 10.20 |
1.15 10.00 |
1.20 12.40 | ||||
1.85 12.00 |
1.20 9.40 |
1.10 10.60 |
1.00 9.80 | |||||
1.35 10.80 |
1.45 12.20 |
1.10 10.40 |
1.15 11.60 | |||||
1.45 10.00 |
1.20 10.30 |
1.05 9.20 |
1.10 10.60 | |||||
1.40 11.00 |
1.40 11.30 |
1.40 13.00 |
1.00 9.20 | |||||
1.45 11.80 |
1.30 11.40 |
1.45 13.50 |
1.45 13.90 | |||||
1.50 12.50 |
1.15 12.80 |
1.30 13.00 |
1.35 12.80 | |||||
1.55 13.40 |
1.30 10.90 |
1.70 14.80 |
1.15 9.30 | |||||
1.40 11.20 |
1.35 11.60 |
1.40 12.30 |
1.10 9.60 | |||||
1.50 11.60 |
1.15 8.50 |
1.45 13.20 |
1.20 12.40 | |||||
1.60 12.60 |
1.35 12.20 |
1.25 12.00 |
1.05 11.20 | |||||
1.70 12.50 |
1.20 9.30 |
1.30 12.80 |
1.10 11.00 | |||||
总和 xi.,yi. |
18.25 141.80 |
15.40 130.80 |
15.65 144.80 |
13.85 133.80 | ||||
平均 |
1.52 11.82 |
1.28 10.84 |
1.30 12.07 |
1.15 1.15 | ||||
协方差分析的计算步骤如下:
(一)求x变量的各项平方和与自由度
1.总平方和及自由度
![]()
![]() =kn-1=4×12-1=47
=kn-1=4×12-1=47
2.处理间平方和与自由度
![]()
![]() =k-1=4-1=3
=k-1=4-1=3
3.处理内平方和与自由度
![]() =
=![]() -
-![]() =1.75-0.83=0.92
=1.75-0.83=0.92
![]() =
=![]() -
-![]() =47-3=44
=47-3=44
(二)求y变量各项平方和与自由度
1.总平方和与自由度
![]()
![]() =kn-1=4×12-1=47
=kn-1=4×12-1=47
2.处理间平方和与自由度
![]()
![]() =k-1=4-1=3
=k-1=4-1=3
3.处理内平方和与自由度
![]() =
=![]() -
-![]() =96.76-11.68=85.08
=96.76-11.68=85.08
![]() =
=![]() -
-![]() =47-3=44
=47-3=44
(三)求x和y两变量的各项离均差乘积和与自由度
1.总乘积和与自由度
![]()
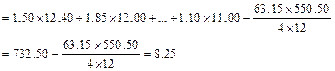
![]() =kn-1=4×12-1=47
=kn-1=4×12-1=47
2.处理间乘积和与自由度
![]()
![]()
=1.64
![]() =k-1=4-1=3
=k-1=4-1=3
3.处理内乘积和与自由度
![]() =
=![]() -
-![]() =8.25-1.64=6.61
=8.25-1.64=6.61
![]() =
=![]() -
-![]() =47-3=44
=47-3=44
平方和、乘积和与自由度的计算结果列于表7-2。
表7-2 x与y的平方和与乘积和表
变异来源 |
df |
|
|
|
处理间(t) |
3 |
0.83 |
11.68 |
1.64 |
处理内(误差)(e) |
44 |
0.92 |
85.08 |
6.61 |
总变异(T) |
47 |
1.75 |
96.76 |
8.25 |
(四)对x和y各作方差分析(表7-3)
表7-3 初生重与50日龄重的方差分析表
变异来源 |
df |
x变量 |
y变量 |
F值 | ||||
SS |
MS |
F |
SS |
MS |
F | |||
处理间 |
3 |
0.83 |
0.28 |
13.33** |
11.68 |
3.89 |
2.02 |
F0.05=2.82 F0.01=4.26 |
处理内(误差) |
44 |
0.92 |
0.021 |
85.08 |
1.93 | |||
总变异 |
47 |
1.75 |
96.76 | |||||
结果表明,4种仔猪平均出生体重存在显著差异,平均体重50天不显著。应该进行协方差分析以消除不同初级体重对测试结果的影响,减少测试误差并揭示可能隐藏的处理之间的显著差异。


