第二节  协方差分析的基本原理 

我们以最简单的情况：一个协变量，单因素的协方差分析为例对协方差分析的基本原理加以说明。

一、统计模型：

在协方差分析中，我们认为每一个因变量的观察值可分解为以下各部分的和：

       （7-9）

其中：第水平的第次观察值。

：水平的次观察的协变量取值。

：的总平均数。

：的总平均数。

：第水平的效应。

：对的线性回归系数。

：随机误差。

需要满足的条件为：

（1）

（2），即Y与X存在线性关系，且各水平回归系数相等，即协变量的影响不随水平的变化而改变。

（3）处理效应之和为0，即：。

上述第三个条件说明该因素为固定因素。若为随机因素，则应该为处理效应的方差为0。模型（7-9）式也可写为：

      ，             （7-10）

这种写法看起来简单一点，它的缺点是不再是Y的总平均值，因为。我们以后的讨论针对（7-9）式进行。

二、协方差分析的统计量：

进行协方差分析需计算以下统计量：

             

             

            

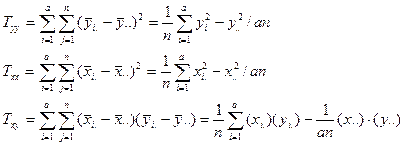
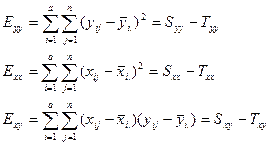
其中S，T，E分别代表总的，处理的和误差的（包括协变量的影响）平方和及交叉乘积和。它们的关系可表示为：

这实际是平方和的分解。同学们可自行证明其交叉项为0。

三、协方差分析的原理：

协方差分析的核心思想是通过对因变量Y进行调整，消去协变量X的影响，从而能对另一因素不同水平的影响进行统计检验。在模型中，各参数的估计量为：

                         

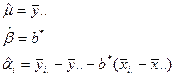
其中。误差平方和为：

它的自由度为：dfe = a(n− 1) − 1。这是因为Syy的自由度为an − 1，Tyy的自由度为a − 1，所以Eyy的自由度为an − 1 − a+ 1 = a(n − 1)，而b*Exy为一个一元回归平方和，自由度为1，所以SSe的自由度为a(n − 1)− 1。

注意上述计算中用的是E而不是S，即对每一个水平分别计算后再加起来的，因此是排除了影响的回归。

我们希望检验：。在此假设下，统计模型变为：

这是一个一元回归问题，此时和的最小二乘估计为：

误差平方和为：

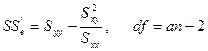
其中为Y对X的回归平方和。

若不成立，则中会有的影响，因此会明显偏大。它们的差就是各对总变差的贡献，自由度为。所以我们可用下述统计量对作检验：

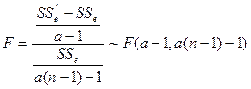         （7-11）

若大于查表得到的上单尾分位数，则拒绝，即各水平效应明显不同。

我们可以把协方差分析与方差分析作一比较：

若不存在协变量影响，即=0，模型变为：

这是单因素方差分析。总变差为Syy，误差平方和为Eyy，处理平方和Tyy = Syy − Eyy，我们用

作统计检验。

若，我们用它对Syy和Eyy作调整：把Eyy调整为SSe作为误差估计，由于又用了一个估计量b*，又减少了一个自由度，SSe的自由度变为； Syy调整为，它与SSe的差作为处理平方和的估计，它的自由度仍为。因此，调整后的统计量变为（7-11）式。

从上面的分析可见，处理平均数实际上包括了处理效应和协变量的回归效应，经过调整后变为：

已消去了协变量的影响，只有处理效应了。它是模型中的最小二乘估计。可以证明它的标准误差为：

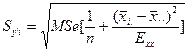
这实际上一元回归中条件均值估计的标准误差。

进行协方差分析应满足的条件有：

（1）

（2）

（3）

在做协方差分析的过程中应对上述条件进行检验。