第八节 非参数检验
非参数检验（Nonparametrictests）是统计分析方法的重要组成部分，与参数检验一起构成统计推断的基本内容。参数测试是在总体分布形式已知时推断总体分布参数的方法，如均值和方差。但在数据分析过程中，由于各种原因，人们往往不能对整体分布模式做出简单的假设，此时参数测试的方法已不再适用。非参数检验是基于这种考虑的一种方法，其中总方差未知或知之甚少，样本数据用于推断总体分布模式。由于非参数测试方法不涉及推理过程中整体分布的参数，因此将其命名为“非参数”检验。非参数检验方法本质上只是检查总体分布的位置（中位数）是相同的，因此对于已知样本的整体分布也可以使用非参数检验，但由于它不能充分利用所有的信息样本中，检验的效率一般低于参数检验方法。
一、配对资料的符号检验
配对数据符号检验是根据样本之间的正负符号数量差异来检验两个总分布位置的异同，而不考虑大小的差异。每对数据之间的差异是“+”正值，负值是“–”。可以假设，如果两个整体分配位置相同，则正数或负数出现次数应该相等。如果不完全相等，至少不应该太大，或者超过一定的临界值，以为两个样本从两个整体差异，分布不同的位置。显然，这个检验将中位数与平均数进行比较，当分布对称时，中位数等于平均数。
配对资料符号检验的基本步骤：
（1）提出无效假设与备择假设
H0：甲、乙两处理差值d总体中位数=0；
H1：甲、乙两处理差值d总体中位数≠0。
此时进行两尾检验。若将H1中的“≠”改为“＜”或“＞”，则进行一尾检验。
（2）计算差值并赋予符号求甲、乙两个处理的配对数据的差值d，d＞0者记为“+”，d＜0者记为“－”，d=0记为“0”。统计“+”、“－”、“0”的个数，分别记为
，令
。检验的统计量为K，等于
、
中的较小者，即
。
（3）统计推断 由n查附表11符号检验用K临界值表（表中P(2)表示两尾概率，用于两尾检验，P(1)表示一尾概率，用于一尾检验）得临界值K0.05(n)，K0.01(n)。如果K＞K0.05(n)，P＞0.05，则不能否定HO，表明两个实验处理差异不显著；如果K0.01(n) ＜K≤K0.05(n) ，0.01＜P≤0.05，则否定H0，接受H1，表明两个实验处理差异显著；如果K≤K0.01(n)，P≤0.01，则否定H0，接受H1，表明两个实验处理差异极显著（注意：当K恰好等于临界K值时，其确切概率常小于附表11中列出的相应概率）。
例5.12 某研究测定了噪声刺激前后15头猪的心率，结果见表5-11。问噪声对猪的心率有无影响？
表5-11 猪噪声刺激前后的心率（次/分钟）
猪 号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
刺激前 |
61 |
70 |
68 |
73 |
85 |
81 |
65 |
62 |
72 |
84 |
76 |
60 |
80 |
79 |
71 |
刺激后 |
75 |
79 |
85 |
77 |
84 |
87 |
88 |
76 |
74 |
81 |
85 |
78 |
88 |
80 |
84 |
差 值 |
-14 |
-9 |
-17 |
-4 |
1 |
-6 |
-23 |
-14 |
-2 |
3 |
-9 |
-18 |
-8 |
-1 |
-13 |
符 号 |
- |
- |
- |
- |
+ |
- |
- |
- |
- |
+ |
- |
- |
- |
- |
- |
这是一个配对资料两尾检验的问题。
1.提出无效假设与备择假设
H0：噪声刺激前后猪的心率差值d总体中位数=0；
H1：噪声刺激前后猪的心率差值d总体中位数≠0。
2.计算差值并赋予符号噪声刺激前后的差值及符号列于表5-11第4行和第5行，从而得
、
，
，
。
3.统计推断当n=15时，查附表11得临界值K0.05(15)=3，K0.01(15)=2，因为K=2= K0.01(15)，P≤0.01，表明噪声刺激对猪的心率影响极显著。
值得注意的是，虽然符号检验方法简单，但是，由于利用的信息较少，所以效率较低，且样本的配对数少于6时，不能检验出差别，在7-12时也不敏感，配对数在20以上时符号检验才较为有用。
二、秩和检验
秩和检验，也称为符号秩和检验（signedrank-sum test），是一种改进的符号检验或Wilcoxon检验，其统计效率远远高于符号检验。由于它比较每对数据差值的符号，还比较每对数据的差值大小等级水平。方法是按照从小到大的顺序排列观察值排列等级，找出等级并进行假设检验。秩和检验与符号检验方法不同，要求差异来自一些对称分布的总体，但并不要求每个差异来自相同的分布。
配对实验资料的符号秩和检验（Wilcoxon配对法）
（一）基本步骤
1.提出无效假设与备择假设
H0：差值d总体的中位数=0；
H1：差值d总体的中位数≠0。
此时进行两尾检验。若将H1中的“≠”改为“＜”或“＞”，则进行一尾检验。
2.编秩次、定符号先求配对数据的差值d，然后按d的绝对值从小到大编秩次。再根据原差值正负在各秩次前标上正负号，若差值d=0，则舍去不记，若有若干个差值d的绝对值相等，则取其平均秩次。
3.确定统计量T 分别计算正秩次及负秩次的和，并以绝对值较小的秩和绝对值为检验的统计量T。
4.统计推断记正、负差值的总个数为n，根据n查附表10(1)符号秩和检验用T临界值表，得T0.05(n)，T0.01(n)。如果T＞T0.05(n) ，P＞0.05，则不能否定H0，表明两个实验处理差异不显著；如果T0.01(n) ＜T≤T0.05(n) ，0.01＜P≤0.05，则否定H0，接受H1，表明两个实验处理差异显著；如果T≤T0.01(n)，P≤0.01，则否定H0，接受H1，表明两个实验处理差异极显著（注意：当T恰好等于临界T值时，其确切概率常小于附表10(1)中列出的相应概率）。
例5.13 在大鼠实验中研究了膳食维生素E缺乏与肝脏中维生素A含量之间的关系。按性别，月龄和体重将大鼠分成10对，将每对中的两只大鼠随机分为正常饲料组和维生素E缺乏饲料组，并测定大鼠肝脏中维生素A的含量表5-12的实验结果。检测两组肝脏维生素A含量是否有显著差异。
表5-12 不同饲料鼠肝维生素A含量资料（国际单位/克）
鼠对别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
正常饲料组 |
3550 |
2000 |
3100 |
3000 |
3950 |
3800 |
3620 |
3750 |
3450 |
3050 |
维生素E缺乏组 |
2450 |
2400 |
3100 |
1800 |
3200 |
3250 |
3620 |
2700 |
2700 |
1750 |
差值di |
1100 |
-400 |
0 |
1200 |
750 |
550 |
0 |
1050 |
750 |
1300 |
秩次 |
+6 |
-1 |
+7 |
+3.5 |
+2 |
+5 |
+3.5 |
+8 |
1.提出无效假设与备择假设
H0：差值d总体的中位数=0；
H1：差值d总体的中位数≠0。
2.编秩次、定符号计算表5-12中配对数据差值di，将d =0的舍去，共有差值n=8个。按绝对值从小到大排列秩次并标上相应的符号，差值绝对值为750的有两个，它们的秩次为3和4，所以其平均秩次为（3+4）/2=3.5，结果见表5-12。
3.确定统计量T 此例，正号有7个，其秩次为2、3.5、3.5、5、6、7、8、秩次和为：2+3.5+3.5+5+6+7=35；
负号只有1个，其秩次为1，秩次和等于1。
负号秩次和较小，所以T=1。
4.统计推断由n=8查附表10(1)得，T0.05(8)=3，T0.01(n)=0，因为T0.01(8)＜T＜T0.05(8)，0.01＜P＜0.05，否定H0，接受H1，表明两个实验处理差异显著。
三、等级相关分析
秩相关是一种分析x、y两个变量的层级是否相关的方法。首先根据x、y两个变量的大小，分别从小到大的系列（rank），再看看这两个变量是否与等级有关。秩相关度的大小和相关性用秩相关系数（coefficientof rank correlation）表示。秩相关系数也被称为秩相关系数。样本等级的相关系数是rs，它是总体等级相关系数
的估计值。等级相关系数rs具有与相关系数r相同的特征，其值在-1和1之间，rs是正相关，rs是负相关，以及rs等于0到零相关。
Spearman等级相关系数基本分析步骤
1.计算等级相关系数rs 先将变量x、y分别由小到大列出等级，相邻两数相同时，取平均等级；再求出每对等级之差d，利用（5-27）式计算等级相关系数：
（5-27）
式中，n为变量的对子数，d秩次之差。
当相同秩次较多时，会影响
值，应采用（5-28）式计算校正的等级相关系数
：
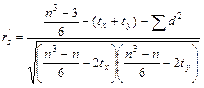（5-28）
式中，
、
的计算公式相同，均为：
。在计算时，
为x变量的相同秩次数；在计算时，为y变量的相同秩次数。
2.rs的显著性检验
（1）提出无效假设与备择假设 H0：
=0；H1：≠0
（2）统计推断 根据n查附表12，得临界
值。若
＜
，P＞0.05，不能否定H0，表明两变量x、y等级相关不显著；若≤＜
，0.01＜P≤0.05，否定H0，接受H1，表明两变量x、y等级相关显著；若≥，P≤0.01，否定H0，接受H1，表明两变量x、y等级相关极显著。
例5.14 研究含有必需氨基酸添加剂的某种饲料的营养价值时，用大白鼠做实验获得了关于进食量（x）和增重（y）的数据，见表5-13。试分析大白鼠的进食量与增重之间有无相关。
表5-13 大白鼠进食量与增重结果及等级相关分析表
鼠号 |
变量x |
变量y |
秩次差 |
秩次差平方 |
进食量（g） 秩次 |
增重（g） 秩次 |
d |
d2 | |
1 |
820 7.5 |
165 7 |
0.5 |
0.25 |
2 |
780 5 |
158 5.5 |
-0.5 |
0.25 |
3 |
720 4 |
130 2 |
2 |
4 |
4 |
867 9 |
180 9 |
0 |
0 |
5 |
690 3 |
134 3 |
0 |
0 |
6 |
787 6 |
167 8 |
-2 |
4 |
7 |
934 10 |
186 10 |
0 |
0 |
8 |
679 2 |
145 4 |
-2 |
4 |
9 |
639 1 |
120 1 |
0 |
0 |
10 |
820 7.5 |
158 5.5 |
2 |
4 |
合 计 |
16.5 |
1.计算等级相关系数rs 对表5-13中各个实验数据分别按进食量与增重从小到大，排列秩次，对数值相同的数据则取平均秩次，如进食量820克的平均秩次为（7+8）/2=7.5。求出进食量的秩次与增重的秩次之差d和秩次差平方d2。利用（5-27）式，得
2.rs的显著性检验此例n=10，查附表12，得=0.794, 因为
＞，P＜0.01，等级相关极显著，表明大白鼠的进食量与增重之间存在着极显著正相关。
