第五节 两个样本平均数的差异显著性检验
在实践中，推断两个样本的平均值的差异是否显著也是很常见的，以查看两个样本的平均值是否相同。对于两个样本平均值之间的差异，实验设计可以分为两种：一是非配对设计或成组设计两样本平均数的差异显著性检；二是配对设计两样本平均数的差异显著性检。
一、非配对设计两样本平均数的差异显著性检验
非配对设计或成组设计意味着测试单元随机分为两组，然后随机应用于两组，只有两个实验进行处理。在这个设计中，两组的实验单元是相互独立的，并且获得的两个样本彼此独立，并且它们的内容不一定相等。非配对设计资料的一般形式见表5-4。
表5-4 非配对设计资料的一般形式
处理 |
观测值xij |
样本含量ni |
平均数 |
总体平均数 |
1 |
x11 x12 … x1n |
n1 |
|
|
2 |
x21 x22 … x2n |
n2 |
|
|
分析两个非配对设计样本之间显著差异的基本步骤如下：
（一）提出无效假设与备择假设 
：
=
，
：≠
（二）计算
值 计算公式为：
（5-11）
其中：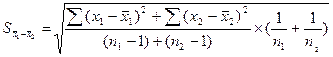
（5-12）
=
=
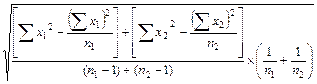
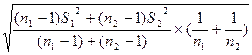
当
时，
=
=
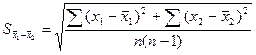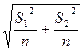（5-13）
为均数差异标准误，
、
，
、
，
、
分别为两样本含量、平均数、均方。
（三）根据df=(n1-1)+(n2-1)，查临界值：
、
，将计算所得t值的绝对值与其比较，作出统计推断。
例5.4 某种猪场分别测定长白后备种猪和蓝塘后备种猪90kg时的背膘厚度，测定结果如表5-5所示。设两品种后备种猪90kg时的背膘厚度值服从正态分布，且方差相等，问该两品种后备种猪90kg时的背膘厚度有无显著差异？
表5-5 长白与蓝塘后备种猪背膘厚度
品种 |
头数 |
背膘厚度（cm） |
长白 |
12 |
1.20、1.32、1.10、1.28、1.35、1.08、1.18、1.25、1.30、1.12、1.19、1.05 |
蓝塘 |
11 |
2.00、1.85、1.60、1.78、1.96、1.88、1.82、1.70、1.68、1.92、1.80 |
1.提出无效假设与备择假设 ：=，：≠
2.计算值 此例=12、=11，经计算得=1.202、
=0.0998、
=0.1096，=1.817、
=0.123、
=0.1508，、分别为两样本离均差平方和。
=
=
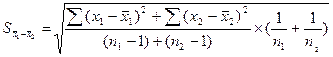
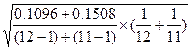
=0.0465
=
**
=（12-1）+（11-1）=21
3.查临界t值，作出统计推断当df=21时，查临界值得：
=2.831，|t|>2.831，P<0.01，否定：=，接受
：≠，表明长白后备种猪与蓝塘后备种猪90kg背膘厚度差异极显著，这里表现为长白后备种猪的背膘厚度极显著地低于蓝塘后备种猪的背膘厚度。
例5.5一家广东黄鸡养殖研究所的养殖对比实验，实验时间为60天，体重增加情况如表5-6所示，问两种饲料对粤黄鸡增重效果是否有显著差异？
表5-6 粤黄鸡饲养实验增重
饲料 |
|
增 重（g） |
A |
8 |
720、710、735、680、690、705、700、705 |
B |
8 |
680、695、700、715、708、685、698、688 |
此例
，经计算得=705.625、=288.839，=696.125、=138.125
1.提出无效假设与备择假设 ：=，：≠
2.计算值，
因为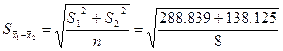 
=7.306
于是 = 
=1.300
=（8-1）+（8-1）=14
3.查临界值，作出统计推断 当df=14时，查临界值得：
=2.145，|t|<2.145，P>0.05，故不能否定无效假设：= ，表明两种饲料饲喂粤黄鸡的增重效果差异不显著，可以认为两种饲料的质量是相同的。
在非配对设计两样本平均数的差异显著性检验中，若总的实验单位数（
）不变，则两样本含量相等比两样本含量不等有较高检验效率，因为此时使最小，从而使的绝对值最大。所以在进行非配对设计时，两样本含量以相同为好。
二、配对设计两样本平均数的差异显著性检验
非配对设计要求测试单位尽可能一致。如果测试单元变异较大，如测试动物的年龄、体重差异等，如果采用上述方法可能会使系统的治疗效果出现误差，降低测试的准确性和准确性。为了消除测试单元不一致对测试结果的影响，正确估计处理效果，减少系统误差，减少测试误差，提高测试的准确性和准确性，可以采用本地控制原理和匹配的设计。
配对设计是指将测试单元二二配对以匹配要求，然后将两个测试单元随机分配给两个处理组。配对的要求是与配对相匹配的两个测试单元的初始条件尽可能一致，并且不同配对的测试单元的初始条件可以改变，并且每一对都重复实验处理。有两种配对方式：自我配对和同源配对。
1.自身配对同一实验单元在两次不同时间前后处理两次，并将其与前后两次观测值进行比较，或与同一实验单元不同部位的观测值或不同方法的观测值进行比较。例如，观察某种疾病动物治疗前后的临床检查结果的变化，并通过两种不同的方法观察动物产品中毒物或药物残留的测定结果的变化。
2.同源配对一对相同来源且具有相同性质的两个个体，例如具有相同畜别、品种、窝别、性别、年龄和体重的一对两个测试动物，然后对成对的两个个体随机进行不同的处理。
在配对设计中，由于测试单元之间存在系统误差，两个测试单元之间存在相似性，数据显著性测试与非配对设计不同。配对设计实验资料的一般形式见表5-7。
表5-7 配对设计实验资料的一般形式
处理 |
观测值xij |
样本含量 |
样本平均数 |
总体平均数 | |||
1 |
x11 |
x12 |
… |
x1n |
n |
|
|
2 |
x21 |
x22 |
… |
x2n |
n |
|
|
dj=x1j-x2j |
d1 |
d2 |
… |
dn |
n | |
|
配对设计两样本平均数差异显著性检验的基本步骤如下：
（一）提出无效假设与备择假设 ：
=0，：≠0，其中为两样本配对数据差值
总体平均数，它等于两样本所属总体平均数与
之差，即=-。所设无效假设、备择假设相当于：=，：≠。
（二）计算值 计算公式为:
, 
（5-14）
式中，
为差异标准误，计算公式为:
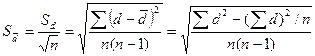（5-15）
为两样本各对数据之差：
，
；
；
为的标准差；
为配对的对子数，即实验的重复数。
（三）查临界值，作出统计推断 根据
查临界值：
和
，将计算所得值的绝对值与其比较，作出推断。
例5.6 用家兔10只实验某批注射液对体温的影响，测定每只家兔注射前后的体温，见表5-8。设体温服从正态分布，问注射前后体温有无显著差异？
表5-8 10只家兔注射前后的体温
兔号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
注射前体温 |
37.8 |
38.2 |
38.0 |
37.6 |
37.9 |
38.1 |
38.2 |
37.5 |
38.5 |
37.9 |
注射后体温 |
37.9 |
39.0 |
38.9 |
38.4 |
37.9 |
39.0 |
39.5 |
38.6 |
38.8 |
39.0 |
|
-0.1 |
-0.8 |
-0.9 |
-0.8 |
0 |
-0.9 |
-1.3 |
-1.1 |
-0.3 |
-1.1 |
1.提出无效假设与备择假设
：=0，即假定注射前后体温无差异
：≠0，即假定注射前后体温有差异
2.计算值 经过计算得
=-0.73，
故 
且 =10-1=9
3.查临界值，作出统计推断由
=9，查值表得：
=3.250，|t|>，P<0.01，否定：=0，接受：≠0，表明家兔注射该批注射液前后体温差异极显著，注射该批注射液可使体温极显著升高。
例5.7 现从8窝仔猪中每窝选出性别相同，体重接近的仔猪两头进行饲料对比实验，将每窝两头仔猪随机分配到两个饲料组中，时间30天，实验结果见表5-9。问两种饲料喂饲仔猪增重有无显著差异？
表5-9 仔猪饲料对比实验 单位：kg
窝号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
甲饲料（ |
10.0 |
11.2 |
11.0 |
12.1 |
10.5 |
9.8 |
11.5 |
10.8 |
乙饲料（ |
9.8 |
10.6 |
9.0 |
10.5 |
9.6 |
9.0 |
10.8 |
9.8 |
|
0.2 |
0.6 |
2.0 |
1.6 |
0.9 |
0.8 |
0.7 |
1.0 |
）
）
1.提出无效假设与备择假设
：=0，即假定两种饲料喂饲仔猪平均增重无差异
：≠0，即假定两种饲料喂饲仔猪平均增重有差异
2.计算值 计算得 =0.975, 
故 
且 =8-1=7
3.查临界
值，作出统计推断由df=7，查值表得：
=3.499，|t|>3.499，P<0.01，表明甲种饲料与乙种饲料喂饲仔猪平均增重差异极显著，这里表现为甲种饲料喂饲仔猪的平均增重极显著高于乙种饲料喂饲的仔猪平均增重。
一般说来，相对于非配对设计，配对设计能够提高实验的精确性。两种方法估计误差的公式为：
非配对设计（）
配对设计
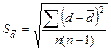
两式中被开方表达式的分母相同。
因为
=
在配对设计中，
和
有同时为正和同时为负的倾向，故
常大于0，
常小于
，这样
常小于
。但并非所有恒大于零，故有时大于，也就是说并非所有的配对设计的实验误差都小于非配对设计的实验误差。这就要求我们在进行配对设计时，配成对子的两个实验单位必须真正符合配对条件，若实验单位不具备配对条件，不要勉强采用配对设计。
此外，还须指出，因为配对设计误差自由度为非配对设计（n1=n2=n）误差自由度的一半，使得配对设计的临界值大于非配对设计的临界值，于是配对设计只有因的减小而使计算的的绝对值增大的程度超过因自由度减小而使临界值增大的程度，才能比非配对设计更有效地发现两样本间的真实差异。
在进行两样本平均数差异显著性检验时，亦有双侧与单侧检验之分。关于单侧检验，只要注意问题的性质、备择假设的建立和临界值的查取就行了，具体计算与双侧检验相同。
