第三节     抽样分布 

前面提到，在统计检验过程中，我们应该建立统计数据，将样本中我们关心的信息集中在一起以便对其进行检验，并且此检验主要通过计算统计对观测值的概率并将其与此进行比较，具有指定标准（即显著性水平）的可能性。为了计算这种可能性，我们需要知道统计学服从的理论分布。由于这些理论分布的推导需要更多的数学知识，而且它们的分布函数和密度函数的数学表达式也是非常复杂的，对于生物学的学生来说，掌握推导过程及这些表达式几乎没有实际用途，所以本书省略这部分，有兴趣的学生可以参考概率论或数理统计的教科书。

下面我们就介绍一些常用统计量的理论分布。如无特别说明，假设所有样本均抽自正态总体。

（1）样本线性函数的分布：

若为一简单随机样本，其总体分布为，统计量为：

其中为常数，则也为正态随机变量，且

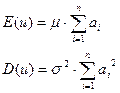                 （5-1）

显然若取=，，则为样本均值。此时

（2）分布：

设相互独立，且同服从，则称随机变量

                 （5-2）

所服从的分布为分布，记为，称为它的自由度。

（3）t分布：

设，，且X，Y互相独立，则称随机变量

                  （5-3）

所服从的分布为t分布，记为。n称为它的自由度。

（4）F分布

设，，且互相独立，则称随机变量

                   （5-4）

所服从的分布为F分布，记为，称为它的自由度。

（5）正态总体样本均值与方差的分布

这一定理及它的推论构成了本章主要内容的理论基础。

定理：若为抽自总体的简单随机样本，定义样本均值为：，样本方差为：，则有：

（1）与相互独立；

（2）                                 （5-5）

（3）                     （5-6）

推论1：统计量

                （5-7）

推论2：若为取自总体的样本，为取自总体的样本，且它们互相独立，则：

               （5-8）

其中S12, S22分别为X1,…,Xm，Y1,…,Yn的样本方差。

推论3：在推论2的条件下，若，则：

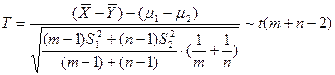        （5-9）

几点说明：

（1）有些书上样本方差定义为：

我们的定义为：

这是因为可证明，而。

（2），但。这可用反证法证明如下：

若，由方差定义，有：

这意味着是一个常量，永不改变。这显然不可能。所以假设不成立。

（3）(5-3）式和(5-7)式中的有不同的统计学意义。（5-3）式中的是的自由度，而(5-7)式中表达式已将它的自由度除掉了，此处除以是因为是总体方差估计值，而的方差为总体方差的倍，因此使用(5-7)式才能将标准化。