第五章 统计假设测验

学习要求：  理解显著性检验的基本思想，了解假设检验可能产生的两类错误。知道两类错误概率，并在较简单的情况能计算两类错误概率，掌握假设检验的基本步骤。了解单个及两个正态总体的均值和方差的假设检验。了解总体分布假设的拟合优度检验法。本章重点：正态总体的参数的假设检验。

参数估计是统计推断的一个方面，另一个是假设检验。这两种推断方法都是对整体参数的研究，但假设检验是研究如何使用样本统计量来检验整体参数所做的假设是否正确，以及它们是否具有某种性质或数量特征。

统计学的核心是如何从一些包含随机误差和不完整的信息中得出科学和正确的结论。一般来说，所谓的信息就是从实验或调查中获得的数据，这显然带有一些我们无法控制和避免的错误。换句话说，即使我们试图保持所有的条件不变，当你重做实验时，结果总是或多或少不同，这是随机误差的影响。至于不完整的信息，这主要是因为我们不可能把所有我们感兴趣的东西去确定。例如，为了研究中国人的身高或某种疾病的流行程度，我们无法衡量整个中国或每个人的身体检查情况，只能按照一定的预定实验方案来选择一些人进行身体检查检查或测量。例如，如果您想判断一批产品是否合格，通常不可能测试每种产品，只有少数产品。在这些情况下，我们收到的信息显然不完整。如何从这些不完整的信息开始，对我们感兴趣的所有事物做出最佳判断？这是统计要解决的主要问题。

一般而言，我们获得的信息包含不确定性，主要来源于以下几个方面：（1）测量过程的随机误差；（2）采样随机性的变化，即仅测量少量样本，则测量服用这批样品的结果与另一批样品的结果不同；（3）我们关切的性质确实发生了某种变化。显然，只有第三个变化是我们想要测试的。统计的任务是对前两种情况是否存在第三种变化给出科学结论。

另一点需要注意的是统计数据可能是错误的。由于用于进行统计判断的信息不完整且出错，我们无法保证统计结论是100％正确的。这与其科学性不矛盾，我们面对的是这样一个不完美的世界，我们对世界的理解只能是一个相对正确的道理，我们只能在此基础上尽可能做出正确的结论。同时，统计学一般不仅给出结论，而且给出了这个结论的可靠性，也就是说，它是正确的概率。这样，我们可以对错误造成的损害进行一些控制。简而言之，统计数据是科学工作者需要从实验数据中得出结论的错误的不可或缺的工具。 

第一节  假设检验的基本问题 

一、假设与假设检验

假设是科学研究中广泛使用的一种方法，它是根据已知的理论和事实对研究对象进行虚假的定性描述。统计学中的假设通常是指统计学上对一般参数的虚假定性描述。在任何研究中，都有必要根据现有的理论和经验对研究结果做出先入为主的假设。这个假设被称为科学假设，统计学上称之为研究假设。证明或伪造这一研究假设的过程称为假设检验。

假设检验过程应首先提出原始假设，例如，正态总体的平均值等于5。该原始假设也被称为0假设（null hypothesis），记录为。同时，必须提出备择假设（或可选假设，alternative hypothesis），例如，总体平均值大于5。备择假设记录为。另一种假设应该由现实世界所代表的方向决定，也就是说，它通常被认为比零假设更符合数据所代表的现实。著名的统计学家费希尔曾经指出：“可以说，每个实验的存在只是为了给事实一个反驳零假设的机会”。“在假设检验中，始终是对假设的直接检验，相反选择一个假设”。原始假设和备择假设是总体分布的两个总体的特征，它们通常基于实际问题的需要和相关的专业理论知识。通常，设定备择假设反映了收集数据的目的。

由于统计假设检验（假设检验）旨在检验差异，因此该检验也称为差异显著检验（重要检验）。假设检验是事先对整体（随机变量）的参数或一般分布进行假设，然后用样本信息来判断假设是否合理，即总体真实情况是否与原始假设一致，用于确定样本是否与我们对整体假设不同的假设检验之间的差异是纯粹的机会突变，还是由我们的假设与整体现实之间的不一致所引起的。该方法的基本思想是当观测数据差异达到一定程度时，将反映与一般理论假设的实际差异，从而拒绝理论假设。

例如，法院正在审判被告人。根据英国法律，被告被推定为无罪，因此原告的律师有责任证明其有罪。在假设检验中，假设被告是无辜的。另一种可供选择的假设是被告人有罪。法庭陪审团应审查各种证据，以确定原告律师是否证实证据与基本无罪推定不符。如果陪审员认为证据与基本的无罪推定不一致，他们会拒绝假设并接受其认为被告有罪的另一种假设。

又如：教育部要检验2007年录取的大学新生平均身高是否达到了4250px标准，这样需要提出原假设（）：2007年大学新生（总体）的平均身高（）是4250px。为了检验这个假设是否正确，需要根据随机取样的原则，从2007年的大学新生总体中选取样本并计算样本的平均高度，以此来检验原假设的正确性。

需要检验的原假设:=4250px，（即大学新生总体平均高度等于4250px）。其备择假设就是:¹4250px，（即大学新生总体平均高度不等于170 cm）。

总体平均数的假设有三种情况：

      （1）:  =；: ≠。

      （2）:  ≥ ；:  < 。

      （3）:  ≤ ；:  > 。

假设检验始于对整体参数的假设，然后收集样本数据，计算样本统计数据，并使用这些数据来确定假设的总体参数在多大程度上可靠，并接受或拒绝原始假设。

假设检验一般分为两类：参数假设检验和非参数假设检验。参数假设检验对变量更为严格，适用于等距变量和比率变量，非参数假设检验对变量更为自由，适用于等距变量和比率变量，以及类变量和顺序变量。 

表5-1 参数和非参数假设检验对变量的要求                                   

变量测量层次	数学性质	描述统计量	适宜的统计分析
分类（nominal）变量	=、≠	众数   频率   列联系数	非参数统计分析
等级（ordinal ）变量	=、≠   >、<	中位数   百分位数   Kendall相关   Spearman相关
等距（interval ）变量	=、≠   >、<   +、-	平均值   方差   Pearson相关	参数统计分析   非参数统计分析
等比（ratio ）变量	=、≠   >、<   +、-   *、/	几何均值   变差系数   多重相关系数

二、假设检验的小概率事件

假设检验的基本思想是：根据统计的小概率原理，采用相反方法的逻辑。小概率原理：实验中的小概率事件几乎是不可能的，如果在一次实验中事件发生。只能认为事件不是来自我们假设的全部，也就是说，我们对整体的假设是不正确的。有理由怀疑假设的有效性，即“拒绝”的假设。

假设检验中的小概率原理：

1.在一次测试中，发生几乎不可能发生的事件的概率。

2.一旦在实验中出现小概率事件，我们有理由拒绝原始假设。

3.小概率由研究人员事先确定。

假设检验的基本逻辑：首先设置（例如，总数的平均值为M），然后根据此来确定抽样分布。如果我们对样本进行随机抽样的概率在基数的抽样分布中出现的可能性很小，我们应该否定原始假设（）并接受研究假设（）。

假设检验的基本原理是：直接检验，从而间接检验，排除抽样误差的可能性。    

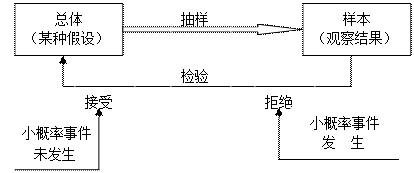
图5-1 小概率原理示意图 

例如，一家制造商声称他的产品合格率很高，可能达到99％，那么随机选择的产品（如100件）产品缺陷的可能性很小，仅为1％。如果制造商的宣传是真实的，那么几乎不可能随机抽取有缺陷的商品。但是，如果发生这种情况，有理由怀疑原来的假设，即产品的缺陷假设只有1％成立，那么就有理由推翻原来的假设，可以使制造商的宣传是虚假的这样的推论。

根据小概率原则可以犯错误！在上述例子中的100个产品中，只有1个产品存在缺陷，如果恰好在单次抽取中抽取，产生错误的概率为1％，这意味着我们要承担1％的风险，一个关于制造商宣传的错误推断。

三、Ⅰ型错误和Ⅱ型错误

由于样本的随机性和局部性，它提供的信息必然是有缺陷的，其缺陷也会传递到假设检验的最终决定中，从而潜在地存在出错的可能性。

在培审团做出决定的情况下，原假设有4种可能的情况（被告无罪）：

（1）对于真相，即被告无罪，陪审团也证实了他的清白和接受。陪审团做出了正确的决定！

（2）确实，被告无罪，但陪审团确认了他的罪过，拒绝了，陪审团做出了错误的决定！

（3）不真实，即被告人有罪，陪审团也证实自己有罪，拒绝，陪审团做出了正确的决定！

（4）不正确，即被告人有罪，但陪审团确认其无罪，接受，陪审团做出了正确的判决！

在上述第（2）和（4）中，陪审团的决定是错误的。

Ⅰ型错误（弃真错误）：原假设本来为真，却错误地否定了。记

上述第（2）种情况就属于弃真错误。

Ⅱ型错误（取伪错误）：原假设非真，但做出接受的选择。记

上述第（4）种情况就属于取伪错误。

犯两错误的概率：在假设检验中，犯Ⅰ型错误（type I error）的概率记为，也称为显著性水平。犯Ⅱ类错误（type II error）的概率记为。 

表5-2 假设检验的四种可能结果                                             

陪审团审判				假设检验
判决	真实的情况			结论	总体参数的实际情况
	无罪	有罪			原假设为真	备择假设为真
无罪	判决正确	判决错误		未拒绝原假设	结论正确	第二类错误
有罪	判决错误	判决正确		拒绝原假设	第一类错误	结论正确

假设检验中犯Ⅰ型错误的概率，称为显著性水平（Level ofSignificance），即指当零假设实际上是正确时，检验统计量落在拒绝域内的概率，通常用（）表示。它体现了对原假设的“保护”程度，水平越小，拒绝原假设要求的理由就越充分，对原假设的保护越严密。的取值一般有1%、5%。这种只对第一类错误的概率加以控制，而不考虑犯第二类错误的概率的检验，成为显著性检验（Significant Testing）。

人们自然希望犯这两类错误的概率越小越好。但对于一定的样本容量n，两类错误有相反的关系（如图5-2所示），减小会引起增大，减少会引起增大。可能带来的后果越严重，危害越大的哪一类错误，在假设检验中作为首要的控制目标！

假设检验中，遵守首先控制犯错误原则大家都在执行这样一个原则。

原因是：原假设是什么常常是明确的，而替换假设是什么常常是模糊的。所以，人们常把我们最关心的问题作为原假设提出，将较严重的错误放到了，这就能够在假设检验中对错误实施有效控制。在处理实际问题时，一般犯弃真错误会造成严重的损失，所以，我们要保护，使它不轻易被拒绝，这就要求应很小，即是一个很小的正数。这类假设检验通常称为显著性假设检验，小正数称为显著性水平或检验水平。 

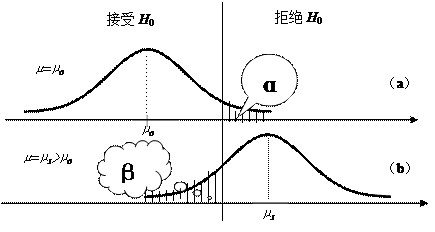
图5-2 假设检验中犯两类错误的关系 

图5-2（a）显示，如果原假设: =为真，样本的统计结果落入阴影中的概率为，若给予拒绝，犯弃真错误的概率为；

图5-2（b）显示，如果原假设: =为伪，因为>，若接受原假设，犯取伪的错误，其概率为。

上图还表明，如果临界点沿水平方向右移，将变小而变大；如果向左移，变大而将变小，从图示上说明了在假设检验中和此消彼长的关系，理论上已经证明，和互为反函数。

若正确，即，图中两曲线应重合。由于统计量时我们拒绝，因此犯第一类错误的概率, 即图中竖线右边阴影部分面积。若错误，即，统计量的真正密度函数曲线为(b)。由于时我们接受，所以犯第二类错误的概率，为线左侧曲线(b)下的面积。

从图5-2中可见：

（1）与是一一对应的。也称为显著水平，因为它也可理解为真值与中值的差异达到什么水平才拒绝。

（2）若与位置不变，右移，则减小，加大；若左移，则增大，减小。因此应根据犯了两类错误后的危害大小来选取适当的值。

（3）不仅依赖于，也依赖于。若很小，则即使不小，也会迅速增大。即若与差异不大，则弄假成真的可能就很大。但由于接近，犯了第二类错误也关系不大。

（4）若已确定，又希望同时减小和，则只能增加样本含量。此时由于统计量的方差减小，曲线变尖，因此，可同时减小。

对于错误来说，可以通过控制显著性水平来减小犯错误的概率。一般而言，如果实验条件控制的较好的话，可以取=0.05；如果实验条件难以控制，则可以取=0.01或更高的显著性水平值。

错误与错误不同，它并不是检验之前规定的。影响的因素主要有三。一是在参数检验中，依赖于参数的实际值与假设值之间的距离。实际值与假设值相差越大，会越小。二是与检验前选定的有关，越小，越大，因此要同时降低和，需要增加样本容量（）。三是当和固定时，根据研究问题性质选择适当的检验类型可以减小。由此可见，对于错误而言，控制是比较困难的。因此一般在规定的下，采用增大样本容量的方法来尽量减小。

称为检验功效或检验力（power of test），也叫把握度。其意义是当两总体确有差别（即成立）时，按水平能发现它们有差别的能力。例如，意味着若两总体确有差别，则理论上平均100次抽样比较中有90次能得出有差别的结论。

四、双侧检验和单侧检验

对总体平均数的假设检验可分为两种类型，即双侧检验（Two-tail Test）和单侧检验（One-tail Test）。

双侧检验。原假设是等于某一数值，只要>或<二者中有一个成立，就否定原假设。即:  =  ，:  ≠。

双侧检验的目的：观察在规定的显著水平上采集的样本的统计数量是否明显高于或低于假设的总体参数。标准正态（或T）分布曲线的2尾区域占据/2，因此具有2个拒绝区域。如果样本统计数据落在任何拒绝区域，则原始假设被拒绝。双侧检验的原理图如图5-3所示。

   

 图5-3 双侧检验 

单侧检验。单侧检验：主要关心带方向性的检验问题。分两种情况：一种是所考察的数值越大越好。另一种是数值越小越好。单侧检验可分为左侧检验和右侧检验两种，它们都只有一个拒绝区域。

左侧检验。假设：:  ≥ ，:  < ，就使用左侧检验。拒绝区域在临界值左端。左侧检验适用于担心样本统计量会显著地低于假设的总体参数的情况。左侧检验的示意图如图5-4所示。   

 图5-4 左侧检验示意图

右侧检验。假设:  ≤ ，:  > 。只要样本平均数显著超过假设的总体参数，就拒绝原假设。拒绝区域是在临界值的右侧。右侧检验的示意图如图5-5所示。

图5-5 右侧检验示意图

表5-3 双侧和单侧检验问题                         

假设	研究的问题
	双侧检验	左侧检验	右侧检验
	：μ=μ0	：μ≥μ0	：μ≤μ0
	：μ≠μ0	：μ＜μ0	：μ＞μ0

双侧检验时拒绝域分为两块，但阴影部分总面积是与单侧检验相同的，因此，从而使增大。这样在相同时，单侧检验的值小于双侧检验, 即单侧检验优于双侧检验。这是因为我们使用了额外的知识排除了一种可能性。

五、假设检验的基本思想

例5.1 已知某罐头厂生产的100g灌装番茄汁中VC的含量服从正态分布。现改变了工艺条件，为了解新工艺改变后VC含量有无变化，现从刚出厂的一批罐头中任取17个，测得VC的含量（单位：mg）为

16 22 21 20 23 21 19 15 13 23 17 20 29 18 22 16 25

根据以往的经验，总体的方差一般不会改变。试问工艺改变后，VC含量的均值有无改变？

分析：需要解决的问题是：如何根据样本判断工艺改变后生产的罐头VC含量是服从的正态分布，还是与过去一样仍然服从的正态分布？即：

首先，原假设：；    备择假设：.

然后，利用样本信息判断以上哪一个假设更可信。（判断所依据的原理是小概率原理，工具是检验统计量。）

假设检验的基本思想：

（1）假设（hypothesis）：对总体的某种论断。

原假设：；    备择假设：.

（2）检验：利用样本信息对假设作出判断，从而作出接受或拒绝的决定。

（3）原理（小概率原理）：小概率事件在一次实验中几乎不可能发生。

（4）工具：检验统计量。

（5）拒绝域：当，则拒绝；

（6）接受域：当，则接受。

（7）思想：假设成立，如果推出不合理的结论，则拒绝；否则，接受。

下面还以例5.1为例，说明假设检验的基本思想和方法。

首先建立假设

：；    ：.

设为一组样本，是它的一次观测值。

由于是的无偏估计量，因此，若正确，则与的偏差一般不应太大，即不应太大；反之，如果特别大，我们就认为不正确，从而拒绝。

考察的大小等价于考察的大小，而的大小是容易考察的。因为，所以，对任意给定的小正数，由于事件“”是概率为的小概率事件，即

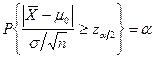
因此，当用样本值代人统计量计算，得到其观测值时，若，则说明在一次抽样中，小概率事件居然发生了。依据小概率原理，不符合原假设，所以有理由拒绝，接受；若，则说明在一次抽样中，小概率事件没发生，符合原假设，所以接受。图示：

图5-6 双侧检验对应的拒绝域 

总结：“不正确”“很大” “很大”“”。

将上述判断过程加以概括，可概括出参数假设检验的一般步骤：

（1）根据所讨论的问题建立原假设及备择假设；

（2）选择合适的检验统计量，并确定其分布；

（3）对预先给定的小概率，由确定临界值；

（4）由样本值具体计算统计量的观测值，并进行判断：若，则拒绝，接受；若，则接受。

关键：第二步找合适的检验统计量。

下面运用一般步骤解决例5.1：

（1）建立假设：，：；

（2）选择检验统计量；

（3）取，查标准正态分布表可得临界值；

（4）具体计算：，，故统计量的观测值

因为，所以拒绝，接受，即认为新工艺改变了罐头VC的含量。